Definite Integration

What is definite integration?

Definite Integration occurs in an alternative version of the Fundamental Theorem of Calculus
This version of the Theorem is the one referred to by most AS/A level textbooks/websites

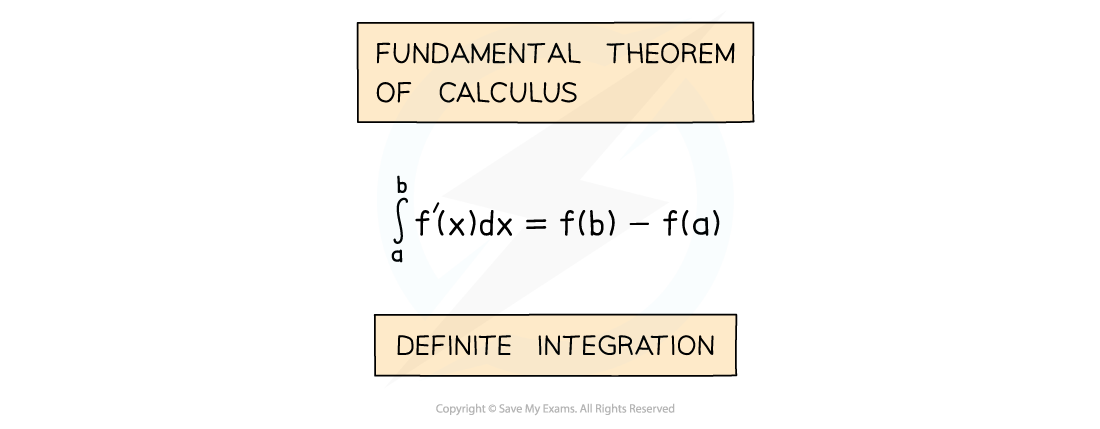
-Notes-fig1, AS & A Level Maths revision notes

a and b are called limits
- a is the lower limit
- b is the upper limit
f’(x) is the derivative of f(x)

What happened to c, the constant of integration?

Notes fig2, AS & A Level Maths revision notes

“+c” would appear in both f(a) and f(b)
- Since we then calculate f(b) – f(a) they cancel each other out
- There would be a “+c” from f(b) and a –“+c” from f(a)
So “+c” is not included with definite integration

How do I find a definite integral?

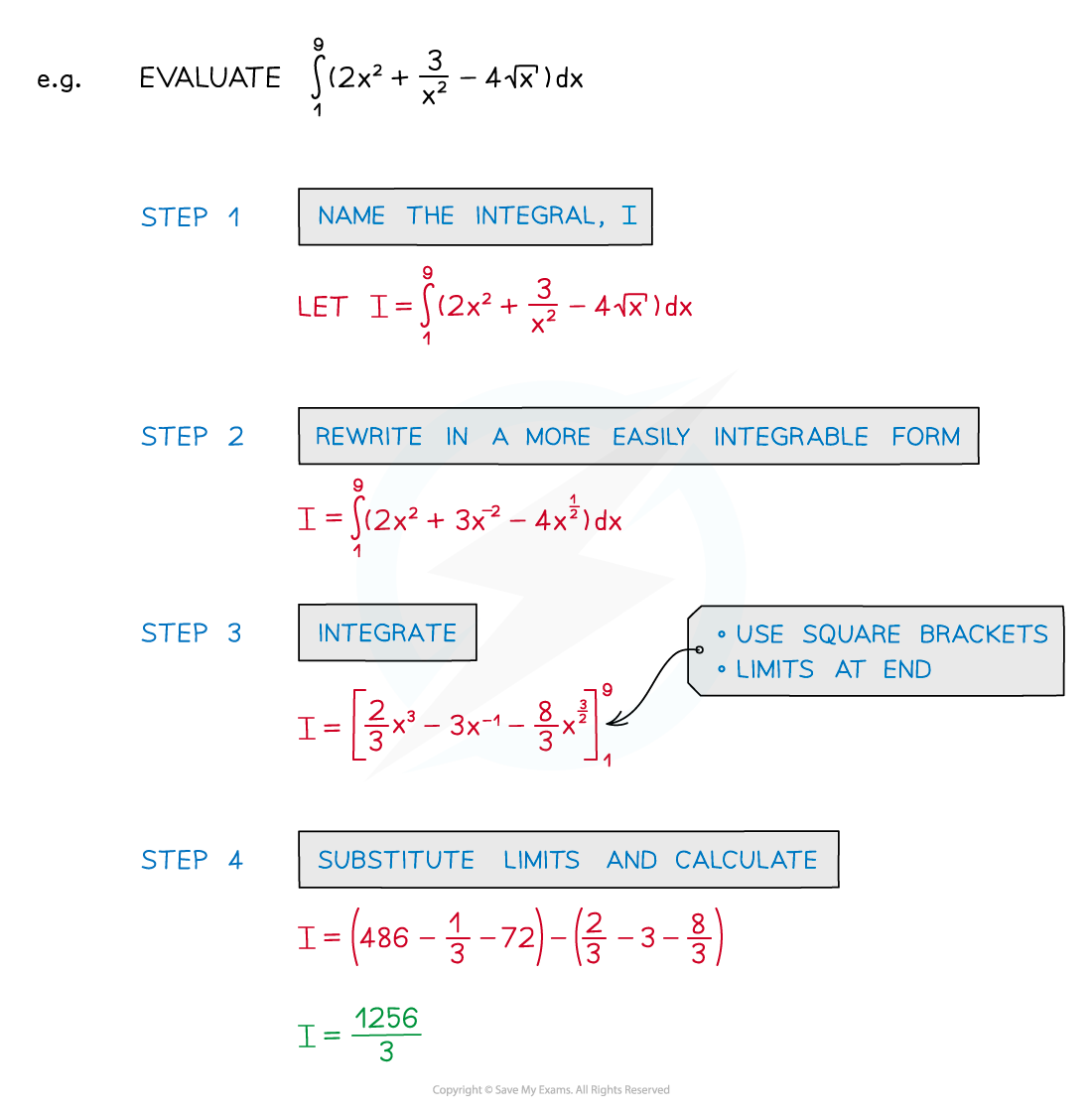
STEP 1: If not given a name, call the integral
- This saves you having to rewrite the whole integral every time!
STEP 2: If necessary rewrite the integral into a more easily integrable form
- Not all functions can be integrated directly
STEP 3: Integrate without applying the limits
- Notation: use square brackets [ ] with limits placed after the end bracket
STEP 4: Substitute the limits into the function and calculate the answer

Notes fig3, A Level & AS Level Pure Maths Revision Notes

Using a calculator

Advanced scientific calculators can work out the values of definite integrals
The button will look similar to:

Notes fig4, AS & A Level Maths revision notes

Notes fig5, AS & A Level Maths revision notes

(Note how the calculator did not return the exact value $(\frac{1256}{3})$ of the integral)

Examiner Tip

Look out for questions that ask you to find an indefinite integral in one part (so “+c” needed), then in a later part use the same integral as a definite integral (where “+c” is not needed).

Worked example

Find the value of

$\int_{2}^{4} 3 x (x^{2} - 2) d x$

Start by expanding the brackets inside the integral

$\int_{2}^{4} (3 x^{3} - 6 x) d x$

Integrate as usual (here it's a 'powers of $x$ ' integration)

Write the answer in square brackets with the integration limits outside

$\begin{array}{rcl} \int_{2}^{4} (3 x^{3} - 6 x) d x & = & {[3 (\frac{x^{3 + 1}}{3 + 1}) - 6 (\frac{x^{1 + 1}}{1 + 1})]}_{2}^{4} \\ = & {[\frac{3}{4} x^{4} - 3 x^{2}]}_{2}^{4} \end{array}$

Now substitute 4 into that function
And subtract from it the function with 2 substituted in

$\begin{array}{rcl} {[\frac{3}{4} x^{4} - 3 x^{2}]}_{2}^{4} & = & (\frac{3}{4} {(4)}^{4} - 3 {(4)}^{2}) - (\frac{3}{4} {(2)}^{4} - 3 (2^{2})) \\ = & (192 - 48) - (12 - 12) \\ = & 144 - 0 \\ = & 144 \end{array}$

$\int_{2}^{4} 3 x (x^{2} - 2) d x = 144$

Definite Integration (AQA AS Maths: Pure)

Revision Note