Permutations & Combinations (CIE AS Maths: Probability & Statistics 1)

Find the number of ways that the letters in SAVEMYEXAMS may be rearranged if

Write down the probability that if the letters in SAVEMYEXAMS are arranged randomly, they will spell out MYEXAMSSAVE.

Three letters are chosen at random from the letters in the word REVISION. Find the number of ways that the selection may contain

Write down the number of arrangements of three letters chosen at random from the word REVISION that have exactly one letter I.

At the Tokyo Olympics, the women’s gymnastics floor finalists were made up of eight competitors from six different nations.  Given that there were two competitors from Russia and two from the USA, and assuming that each competitor had an equal chance of winning,

A farm has a new litter of puppies.  Two of the puppies are classed as mostly white, four are mostly black, and five are classed as black and white mixed.  

Five of the puppies are selected at random.  Find the number of ways in which the selection might contain:

A pool table has fifteen different balls including the black ball.  

Given that the black ball is the last to be potted and the rest of the balls are potted one at a time in a random order, in how many ways can the fifteen balls be potted?

The other fourteen balls consist of seven pairs of different coloured balls.  One of each pair has a stripe across it and the other has a spot on it.  

Given that the black ball is still the last to be potted, in how many ways can the fifteen balls be potted one at a time if

Ms Aiba has twelve different maths textbooks on her classroom bookshelf.  Five of them are Statistics textbooks and the other seven are Pure Mathematics textbooks.  Determine the number of different ways that the books can be arranged on the shelf if

Eight cards are numbered 1, 2, 2, 3, 4, 4, 4 and 5.  All eight cards are placed randomly in a line to make an 8-digit number.

Determine the number of different numbers that can be made if the 8-digit number is

Write down the probability that the 8-digit number made when all eight cards are placed in a line is an odd number greater than 50 000 000.

Riley is going on holiday and is allowed to bring along four of his toys.  At home he has nine different plastic dinosaurs, six different toy cars, and five different wooden reptiles. 

How many different selections of his toys can he make if he chooses at least one of each type of toy?

Riley can’t decide so he persuades his parents to allow him to bring along five toys instead.  

Given that he brings more plastic dinosaurs than any other type of toy, how many different selections can he make now?

How many ways are there to rearrange the ten letters in the word

How many ways are there to rearrange the ten letters in the word if

Find the probability that if the ten letters in the word are arranged randomly, the four vowels will not all be together.

Four letters are chosen at random from the ten letters in the word . Find the number of ways that the selection may contain

In how many distinct ways can four out of the ten letters of the word be arranged if in each case all four letters are different from each other?

A mixed relay team must consist of four competitors two of whom must be male and two of whom must be female.  There are nine men and six women trying out for a place on a new team.  

During the try-outs the fifteen candidates are split into three groups of four and one group of three. How many ways can this be done if the candidates are divided randomly?

Two of the candidates are brother and sister and have agreed they will only be in the final relay team if they are both successful.  How many ways can the final relay team be chosen if the brother and sister are either both in or both out?  

An examination paper consists of four questions in section A and eight questions in section B.  Candidates must answer five questions from the paper in any order.  

Find the number of ways a candidate can choose their questions if

Candidates are now told that if they choose question 1 from section A they cannot choose any other question from section A. However if they do not choose question 1 from section A then they must choose at least two questions from section A and answer question 1 from section B.  In how many ways can a candidate choose their questions under these restrictions?

Dylan is preparing a playlist for his friend’s birthday party.  Dylan chooses 5 different afrobeats tracks, 3 different blues tracks, 3 different country songs and 8 different drum and bass songs.  

In how many different orders can Dylan play the songs if

Whilst at the party a friend likes Dylan’s music and decides to make a playlist of their own.  The friend only has space for twelve songs on their computer.  In how many ways can Dylan’s friend arrange twelve out of the nineteen songs if they decide to have two blues songs first, followed by alternating afrobeats and drum and bass songs?

In his classroom Mr Roland has seven different books about GeoGebra, five different books about football and three identical Mathematics textbooks. 

In how many ways could Mr Roland organise the books on his bookshelf if

Mr Roland’s young son selects three of the books at random to sit on whilst doing his homework. How many different selections from the fifteen books are there if

Nine cards are numbered 1, 2, 2, 3, 5, 5, 5, 6 and 8.  

The nine cards are placed randomly in a line. In how many ways can this be done if

Four of the nine cards are chosen at random and placed in a line to make a 4-digit code. Find the number of ways the code can be made if

Helen is researching three different types of trees for a biology project.  She has collected samples from four different acacia trees, two different banyan trees and three different cedar trees.  She needs to choose six of the tree samples to take to a school science fair.  

How many different selections of the tree samples may be made if if she must have at least one cedar tree sample but cannot take more than three of any type?

Helen decides to take three acacia samples, two banyan samples and one cedar sample.  

In how many different orders can she arrange these samples in a row if the two banyan samples cannot be next to each other? 

How many ways are there to rearrange the twelve letters in the word if the arrangement must start and end with the letter ?

How many ways are there to rearrange the twelve letters in the word if the two are together and the three are not all together?

Taking the vowels in the English alphabet to be find the probability that a random arrangement of the twelve letters in the word begins with a vowel.

Four letters are chosen at random from the nine letters in the word Find the number of ways that the selection may contain: 

(i)   no Ls and exactly one E 

(ii)   no Ls.

Find the probability that, in a random arrangement of all nine letters in the word , all of the Es are separated by at least one letter.

Ahmed is playing a game with the following nine cards:

Ahmed arranges the cards to form a 9-digit number. How many different 9-digit numbers can be made if the number is a multiple of five and the circular cards are not all together?

Ahmed chooses one triangular card, one circular card and one rectangular card at random and arranges them to make a 3-digit code. How many different 3-digit codes could Ahmed make?

Jonni always struggles to decide which combination of fillings, sides and sauces he wants to put in his sandwich at his favourite sandwich shop.  The available options are listed below: 

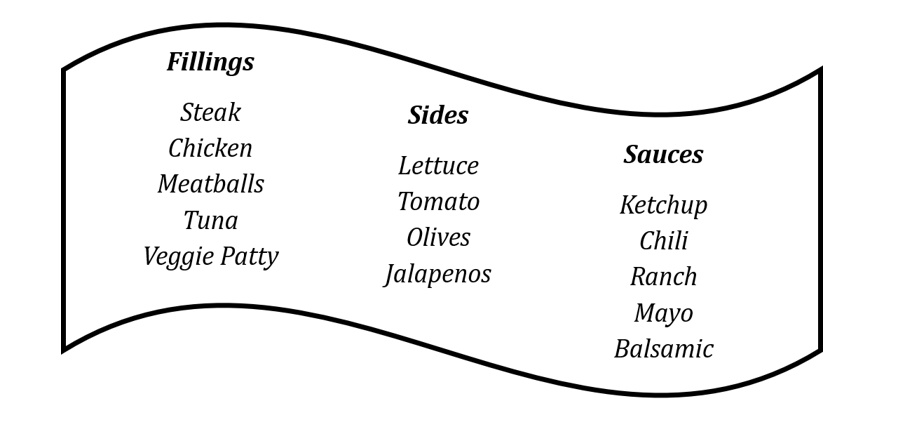
To avoid having to make up his mind, each day Jonni instead sets himself a rule for how many of each option he will put in his sandwich, and then uses an app he has designed to choose one sandwich at random from among those that his rule allows.  Note that choosing the same filling, side or sauce more than once is never allowed. 

If Jonni’s rule on a given day is that he will have one filling, three sides and one type of sauce in his sandwich, find the probability that Jonni has either steak or chicken in his sandwich.

If Jonni’s rule on a given day is that he will have two fillings, one side and three types of sauce in his sandwich, find the probability that he gets either tuna with tomato, or jalapenos with ketchup and mayo, as a part of his sandwich choice.

Twenty-six people are travelling on an airplane.  Seven of them are businesspeople on their way to a facilities management conference.  Three of them are spies on their way to take up positions as ‘consular officials’ in an unnamed embassy.  The other sixteen are cryptozoologists on their way to follow up some clues regarding a recent unicorn sighting.  These passengers have been randomly allocated the seats from 26A to 29E inclusive, as depicted in the diagram below. 

Find the number of ways that all twenty-six people could be seated on the plane if the three spies are all sat in the back row and the seven businesspeople are all in seats by a window.

Given that each of the seven window seats has a cryptozoologist in it, find the probability that the three spies are not all sat together in one of the groups of three seats in between the two aisles.

The following four family groups, consisting of 6 adults and 12 children in total, are all going to the cinema together: 

• Mr and Mrs Mitchell and their two children 

• Mrs and Mrs Lee and their four children 

• Mr Kim and his three children 

• Ms Miller and her three children 

Find the number of different ways that all 18 people can sit in a row of 18 seats if

(i)   no adults are sat next to each other 

(ii)   each family group sits together.

If instead the 18 people are sat randomly in three rows of six, what is the probability that all of the adults will be sat in the back row?

The diagram below shows part of a train carriage.  There are twenty-eight seats consisting of twenty normal seats, S, and eight table seats, T.  In this part of the train carriage there is a group of twelve schoolchildren and two teachers, along with a married couple, four businessmen, and three backpackers.

Find the number of ways that the passengers could be arranged in this part of the train carriage if

Given that everybody is arranged completely at random within this part of the train carriage, find the probability that