Did this video help you?
Stem and Leaf Diagrams (CIE AS Maths: Probability & Statistics 1): Revision Note
Stem and Leaf Diagrams
What is a stem and leaf diagram?
- A stem and leaf diagram shows ALL RAW data and groups it into class intervals
- Stem and leaf diagrams lend themselves to two-digit data but can be used with three-digit data, rarely more

- The numbers in brackets indicate how many values are in that class interval
- These are not always included but can be useful when there is a large amount of data to display
How do I draw a stem and leaf diagram?
- Identify the stems and the leaves
- Leaves would always be single digits
- the number 2 would be represented by 12 | 2
- Leaves would always be single digits
- If starting from unordered data draw two diagrams
- The first diagram should get the data into the right format
-
- i.e. a list of stems with their corresponding leaves
-
- The second diagram should have stems and leaves in order, with a key
- This helps accuracy as values are less likely to be missed out
- The first diagram should get the data into the right format
What are stem and leaf diagrams used for?
- The data is arranged into classes so at a glance it is possible to see the modal class interval
- As the data is in order the median, quartiles, maximum and minimum can be identified easily
- Check you can do this – find the minimum, maximum, median and upper and lower quartiles from the stem and leaf diagram at the start of this revision note
- Note that these five values are those needed in order to construct a box‑and-whisker diagram (box plot)
- Outliers, once defined, can be easily identified and removed
What about back-to-back stem and leaf diagrams?
- These are used when it is helpful for the data to be split into two comparable categories such as boy/girl, child/adult, UK/non-UK. Etc

- Note that the leaves on the left-hand side of the stems (Boys) increase from the centre outwards
Are there any variations on stem and leaf diagrams?
- There are a few minor variations on stem and leaf diagrams that you may see online or in different textbooks

- Some or all the different/extra features in the diagram above may appear
- These differences can be applied to back-to-back stem and leaf diagrams
- With large amounts of data, the stems may be split into two rows
- Every stem will be listed twice
- The first row for a stem will contain leaves 0 - 4
- The second row will contain leaves 5 - 9
What might I be asked to do with a stem and leaf diagram?
- You may be asked to draw or complete a stem and leaf diagram
- Find statistical measures – median, quartiles and interquartile range in particular
- From which you may be required to draw a box-and-whisker diagram
- Identify and remove outliers
- Compare data shown by stem and leaf diagrams (either separate or back-to-back); comment on two things and each should be in both terms of the maths and the context of the question
- a comment about average (use median)
e.g. the girls’ median of 88% was higher than the boys’ median of 65% so on average the girls performed better on the test
-
- a comment about variation (spread) (use interquartile range)
e.g. the girls’ interquartile range of 30% was greater than the boys’ 15% so the boys had more consistent scores on the test
- Analyse what would happen to statistical measures such as the median and quartiles if a value changed or a new value were to be added to the data
Worked example
The following stem and leaf diagrams show the times taken by some children and adults to complete a level on a computer game.

2 | 3 represents a time of 23 seconds
Briefly explain whether adding these times would change the adults’ median time.

Briefly explain whether adding these times would change the adults’ median time.
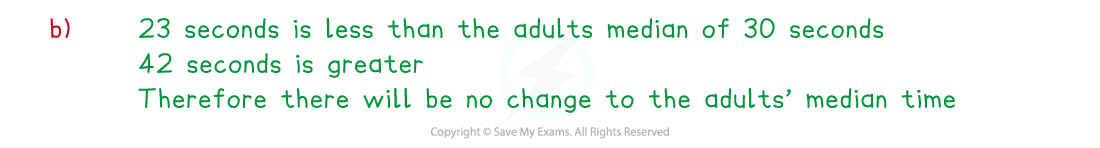
Examiner Tip
- Accuracy is important
- (Lightly) tick off values as you add them to a stem and leaf diagram
- Check you have the right number of data values in total on your diagram
- Other checks can include ensuring the median has the same number of values either side of it

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
