Working with Vectors (Edexcel AS Maths): Revision Note

Working with Vectors

Vectors are used throughout mechanics to describe forces and motion

 How are Vectors used in Mechanics?

• Vector questions are often embedded in a Mechanics context

• Vectors will most commonly represent forces, accelerations or velocities, they can also represent displacement

• Newton’s Second Law is essential

  • Remember that and (force and acceleration) are vectors, while  (mass) is a scalar

• When a particle is in equilibrium, the vector sum of the forces on it is equal to zero

What is vector notation?

• There are two vector notations used in A level mathematics:

  • Column vectors: This is one number written above the other enclosed in brackets,
    
    e.g. The (column) vector meaning 3 units in the positive horizontal (x) direction (i.e., right) and 2 units in the negative vertical (y ) direction (i.e., down) can be written as:

  

  • i and j notation: i and j are unit vectors (they have magnitude 1) in the positive horizontal and positive vertical directions respectively
    
    e.g. The vector (-4i + 3j) would mean 4 units in the negative horizontal (x) direction (i.e. left) and 3 units in the positive vertical (y) direction (i.e. up)

• As they are vectors, i and j are displayed in bold in textbooks and online but in handwriting they would be underlined (i and j)

Calculating Resultant Vectors:

• Both column vectors and i, j notation can be used for calculating resultant vectors

• Adding vectors together gives the resultant vector

• This is the same when adding force vectors; the resultant force is simply the force vectors added together

• Forces in equilibrium have a resultant force equal to zero

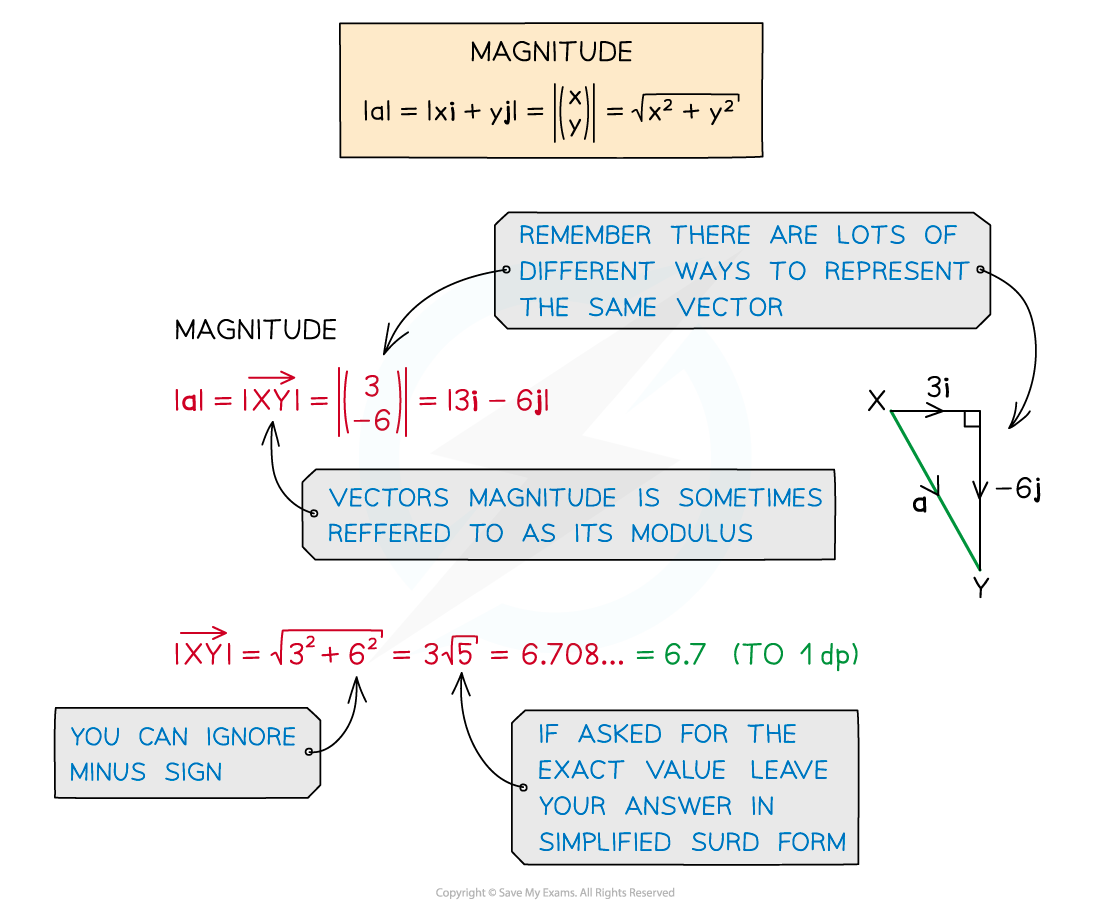
Calculating Magnitude and Direction:

• Pythagoras is used to find the magnitude of a vector.

• Trigonometry is used to find the direction of a vector

• You may be asked for the direction as a bearing. The unit vector j can be used to represent north and the unit vector i can be used to represent east.

  • In the case where k > 0

    • If a particle is moving north then its velocity will have a vector of kj

    • if a particle A is due south of another particle B then the displacement vector from B to A will have the form -kj

    • If a particle is moving east then its velocity will have a vector of ki

    • if a particle A is due west of another particle B then the displacement vector from B to A will have the form -ki

  • If the position vectors of two particles have the same j component, then the particle with the greater i component will be positioned due east of the other

  • If the position vector of a particle has equal i and j components then it is positioned due north - east of the origin

    • if a particle A is north – east of another particle B then the displacement vector from B to A will have equal i and j components

Resolving Vectors:

• Resolving a vector means writing it in component form (as i and j components)

• Given the magnitude and direction of a vector you can work out its components and vice versa