Quadratic Trigonometric Equations (AQA AS Maths) : Revision Note
Did this video help you?
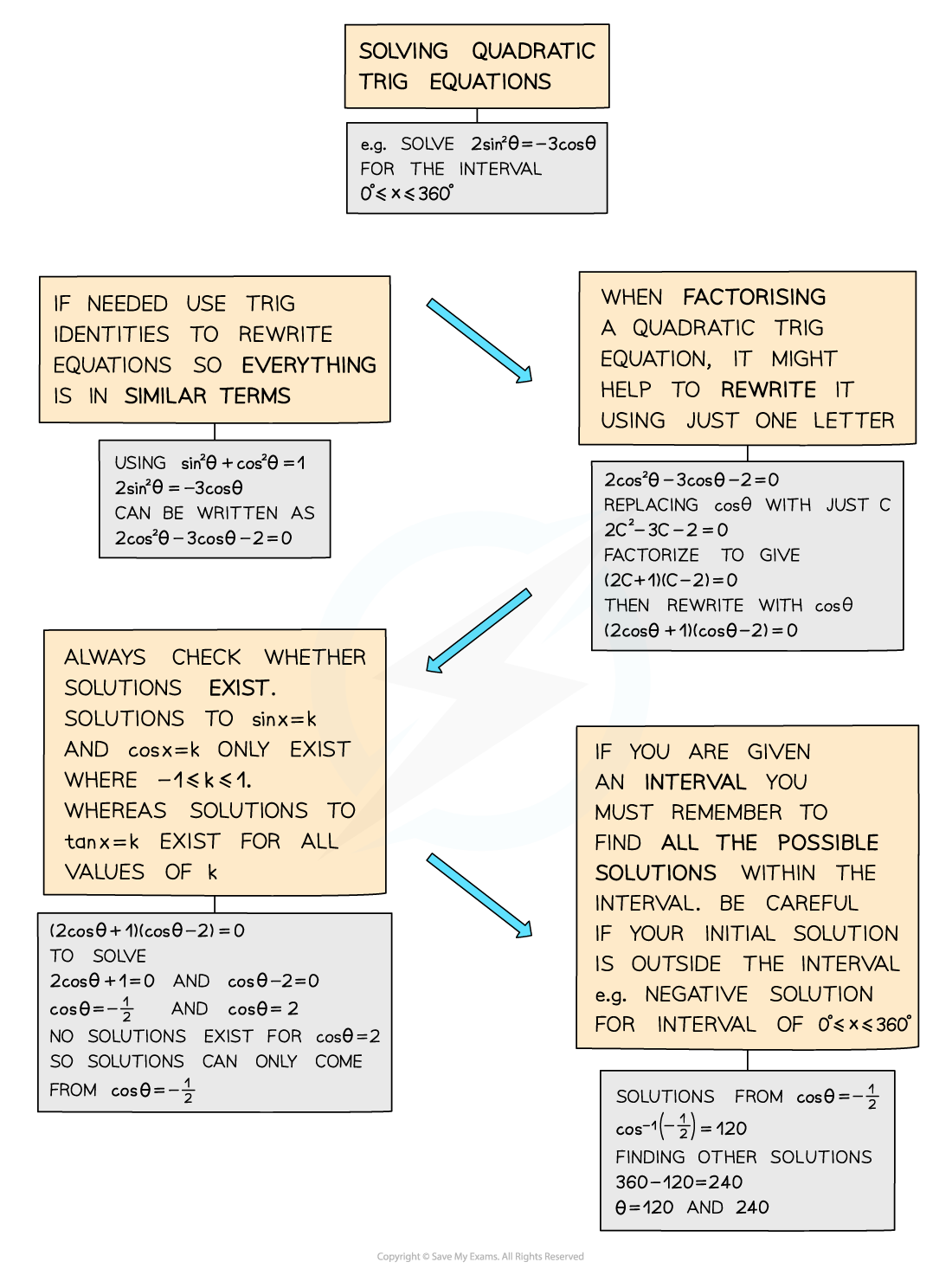
Quadratic Trigonometric Equations
Solving quadratic trigonometric equations
If an equation involves sin2θ or cos2θ then it is a quadratic trigonometric equation
These can be solved by factorising and/or using trigonometric identities (see Trigonometry – Simple Identities)
As a quadratic can result in two solutions, will need to consider whether each solution exists and then find all solutions within a given interval for each
Examiner Tips and Tricks
Sketch the appropriate sin, cos, tan graph to ensure you find ALL solutions within the given interval, and be super-careful if you get a negative solution but have a positive interval.
For example, for an equation, in the interval 0° ≤ x ≤ 360°, with solution sin x = ‑¼ then sin‑1(‑¼) = -14.5 (to 1d.p.), which is not between 0 and 360 – by sketching the graph you’ll be able to spot the two solutions will be 180 + 14.5 and 360 ‑ 14.5.
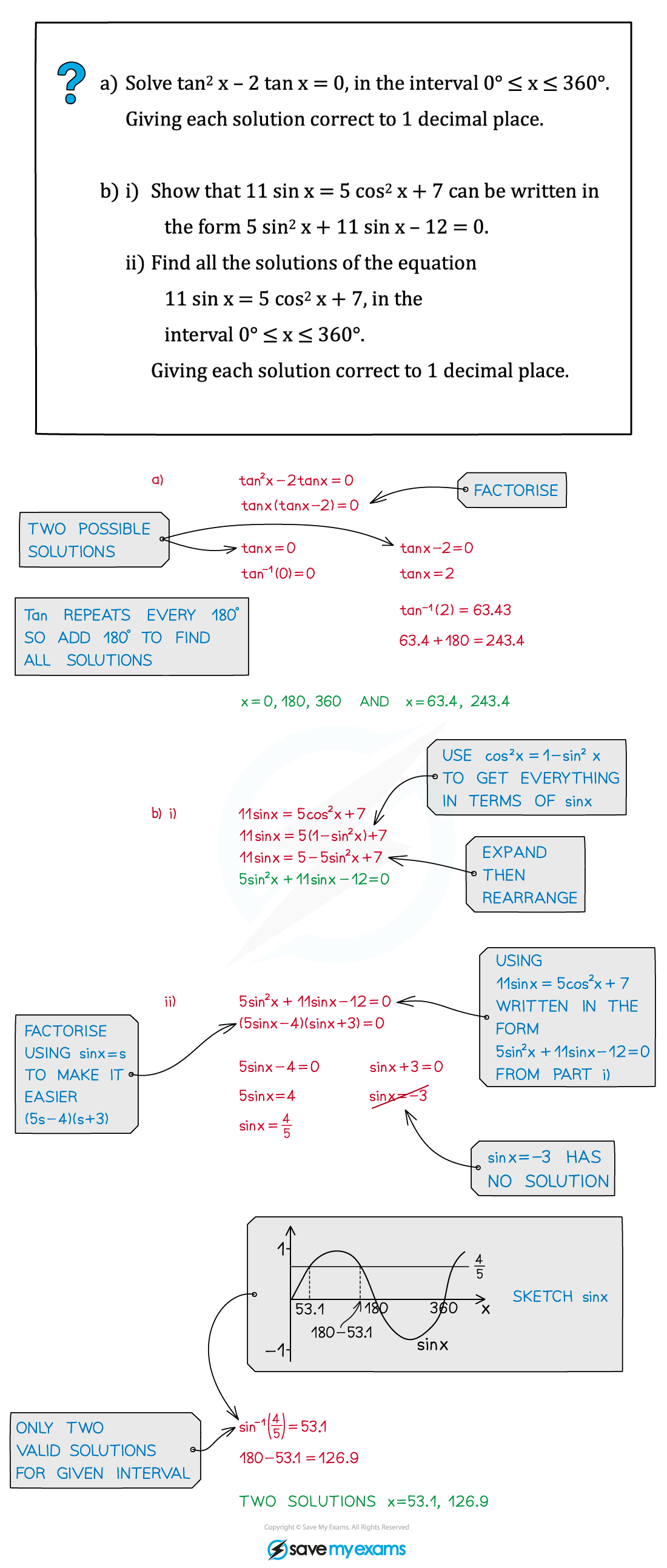
Worked Example

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
