Equilibrium in 2D (AQA AS Maths) : Revision Note
Did this video help you?
Equilibrium in 2D
What does two dimensions (2D) mean in mechanics?
In two dimensions, a particle may be considered as existing and being able to move around two-dimensional space rather than in a single straight line (1D)
This 2D space is called a plane – so you may see the 0xy plane mentioned
The directions of the two dimensions are chosen so that they are perpendicular to each other
The two directions are usually
horizontal and vertical, or
parallel and perpendicular to an inclined plane
What is the resultant force in 2D and an unbalanced force in 2D?
The resultant force in 2D is the sum of forces acting on a particle but this will now need to be considered in two parts – one for each direction
An unbalanced force is a force acting on a particle that whereby one or both parts are not cancelled by another force acting in the opposite direction
So a non-zero resultant force will be non-zero in at least one of the two dimensions, is therefore unbalanced and the particle will accelerate
What does equilibrium in 2D mean?
In two dimensions a particle is in equilibrium if the resultant force acting on it is zero
For example, if the two dimensions involved are the horizontal and vertical directions, a particle will be in equilibrium if any forces acting left are balanced by any forces acting right and any forces acting up are balanced by any forces acting down
When a particle has several forces (at least 3 – have a think as to why!) acting on it – and it is in equilibrium – the forces can be drawn “nose-to-tail” such that they form a polygon

Worked Example
A particle of mass 2 kg is suspended in the air by three strings, one vertical and two horizontal. The particle is in equilibrium and the magnitudes of the tensions in the strings are illustrated in the diagram below.
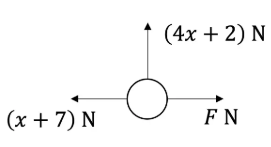
(a) Write down the resultant forces acting on the particle in both the horizontal and vertical directions.

(b) Find the value of F.
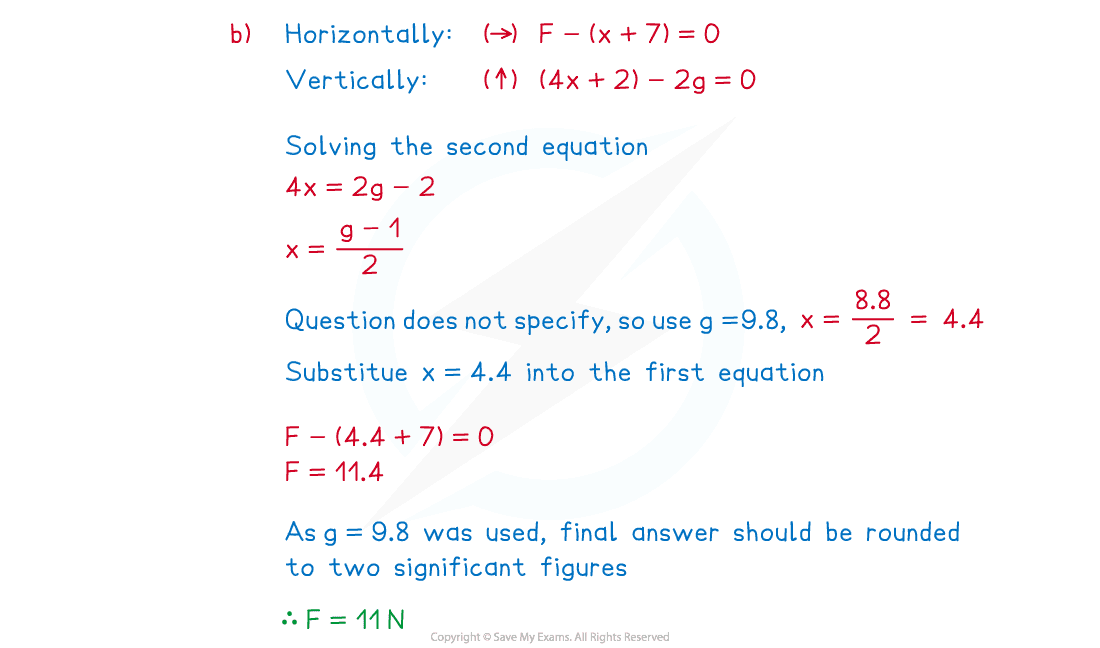
Examiner Tips and Tricks
Fnet is often used for resultant force in equations.
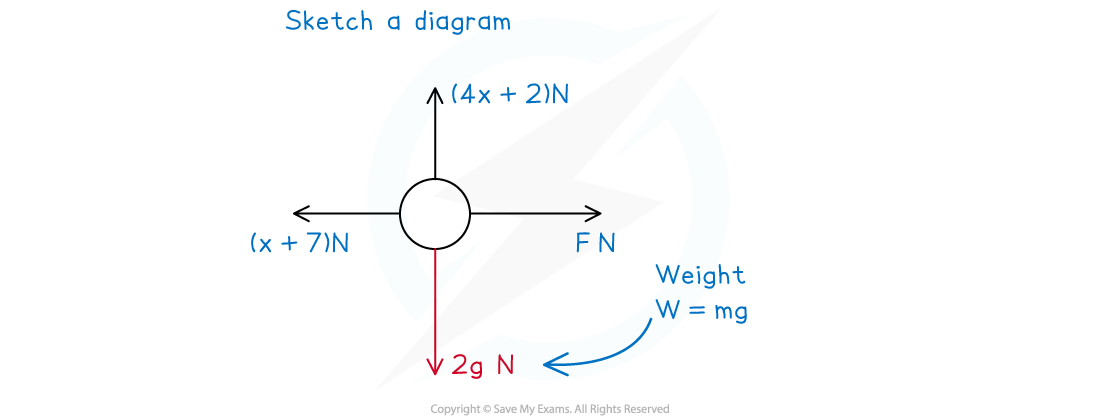
Sketching diagrams, or adding to any given in a question, can help you to understand a problem and pick up some marks.
Unless told otherwise, use g = 9.8 m s-2 rounding your final answer to 2 s. f.; if directed to use g = 10 m s-2 then round your final answer to one 1 s. f.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
