Error & Uncertainty (Edexcel AS Chemistry): Revision Note

Error & Uncertainty

• An error is the difference between a value or quantity obtained in an experiment and an accepted or literature value for an experiment

• There are two types of errors in experiments, random errors and systematic errors

Random Errors

• When you are reading an instrument and estimate the final digit, there is an equal chance that you may read it slightly too high or slightly too low

  • This is a random error

• Random errors are can be affected by:

  • How easily the instrument or scale is to read

  • The person reading the scale poorly

  • Changes in the environment, for example

    • fluctuations in the temperature of the lab

    • air currents in the room

• Random errors will pull a result away from an accepted value in either direction (either too high or too low)

• Repeating the experiment and working with the mean average of the results can help to reduce the effects of random errors

Systematic Errors

• Systematic errors are errors that occur as a result of a faulty or poorly designed experimental procedure

• Systematic errors will always pull the result away from the accepted value in the same direction (always too high or always too low)

• For example,

  • If you forget to zero an electronic balance (using the tare button) the mass weighings will always be higher than they should be

  • If you don't read the volume in a burette at eye level, the volumes will always be smaller than they should be due to a parallax error

  • If you fail to keep a cap on a spirit burner in a calorimetry experiment, the alcohol will evaporate and give you a larger mass loss

• Repeating the experiment and working with the average value will not remove any systematic errors

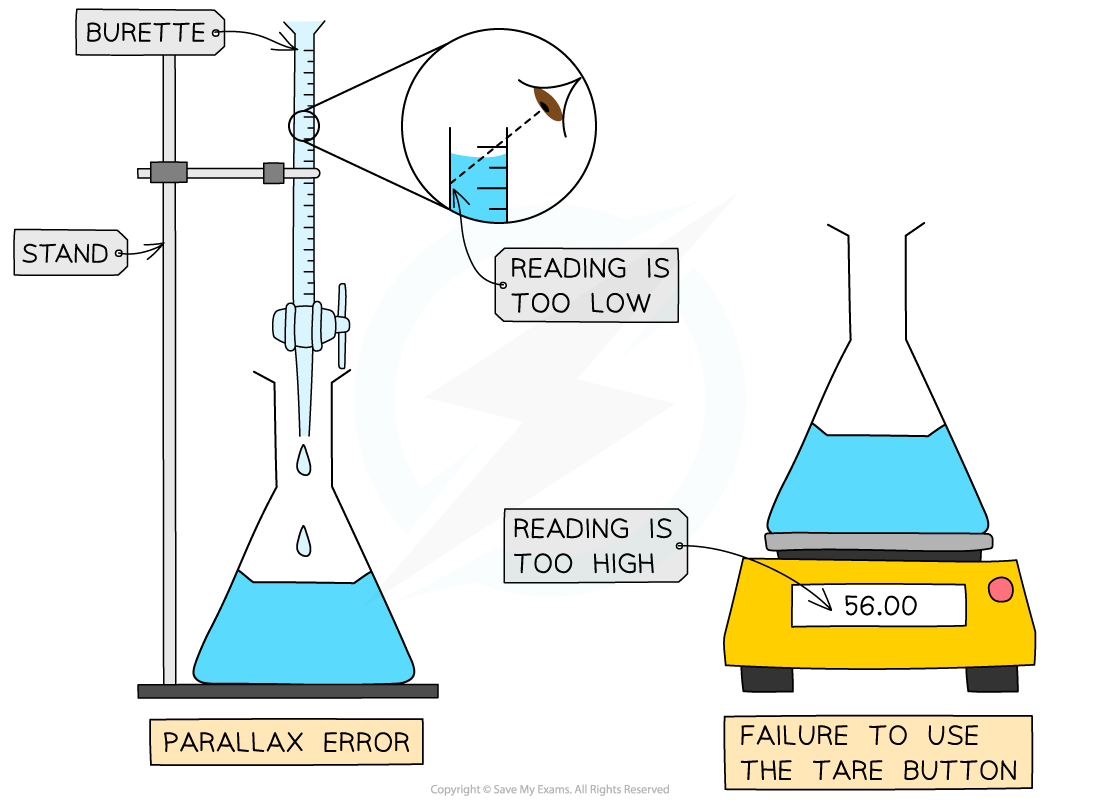
Systematic errors

Percentage Uncertainties

• Percentage uncertainties are a way to compare the significance of an absolute uncertainty on a measurement

• This is not to be confused with percentage error, which is a comparison of a result to a literature value

• The formula for calculating percentage uncertainty is as follows:

Percentage uncertainty = 

• Some examples of percentage uncertainty calculations for common laboratory apparatus:

Calculating Percentage Uncertainty

Adding or subtracting measurements

• When you are adding or subtracting two measurements then you add together the absolute measurement uncertainties

• For example,

  • Using a balance to measure the initial and final mass of a container

  • Using a thermometer for the measurement of the temperature at the start and the end

  • Using a burette to find the initial reading and final reading

• In all these examples you have to read the instrument twice to obtain the quantity

• If each you time you read the instrument the measurement is 'out' by the stated uncertainty, then your final quantity is potentially 'out' by twice the uncertainty

Multiplying or dividing measurements

• When you multiply or divide experimental measurements then you add together the percentage uncertainties

• You can then calculate the absolute uncertainty from the sum of the percentage uncertainties