Equilibrium Constants, Kc & Kp (CIE AS Chemistry)

Equilibrium expression & constant

• The equilibrium expression is an expression that links the equilibrium constant, K_c, to the concentrations of reactants and products at equilibrium taking the stoichiometry of the equation into account
• So, for a given reaction:

aA + bB ⇌ cC + dD

• K_c is defined as:

• Where:
  • [A] and [B] are the equilibrium concentrations of A and B, in mol dm^-3 
  • [C] and [D] are the equilibrium concentrations of C and D, in mol dm^-3
  • a, b, c and d are the respective number of moles of each reactant and product 

• Solids are ignored in equilibrium expressions
• The K_c of a reaction is specific and only changes if the temperature of the reaction changes

Partial pressure

• For reactions involving mixtures of gases, the equilibrium constant K_p is used as it is easier to measure the pressure than the concentration for gases
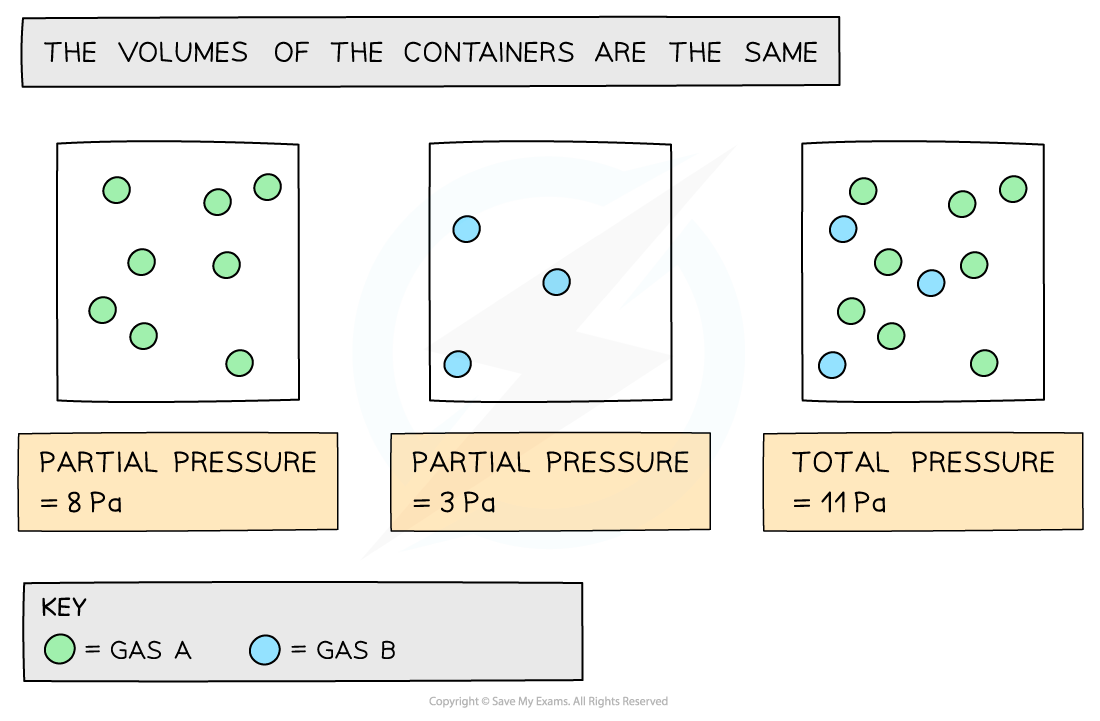
• The partial pressure of a gas is the pressure that the gas would have if it was in the container all by itself
• The total pressure is the sum of the partial pressure:

P_total = P_A + P_B + P_C + .......

• • P_total = total pressure
  • P_A, P_B, P_C = partial pressures

 How partial pressures contribute to total pressure

Partial pressures can be added together to calculate the total pressure

Mole fraction

• The mole fraction of a gas is the ratio of moles of a particular gas to the total number of moles of gas present

• To calculate the partial pressures of each gas the following relationship can be used:

• The sum of the mole fractions should add up to 1.00, while the sum of the partial pressures should add up to the total pressure

Equilibrium expressions involving partial pressures

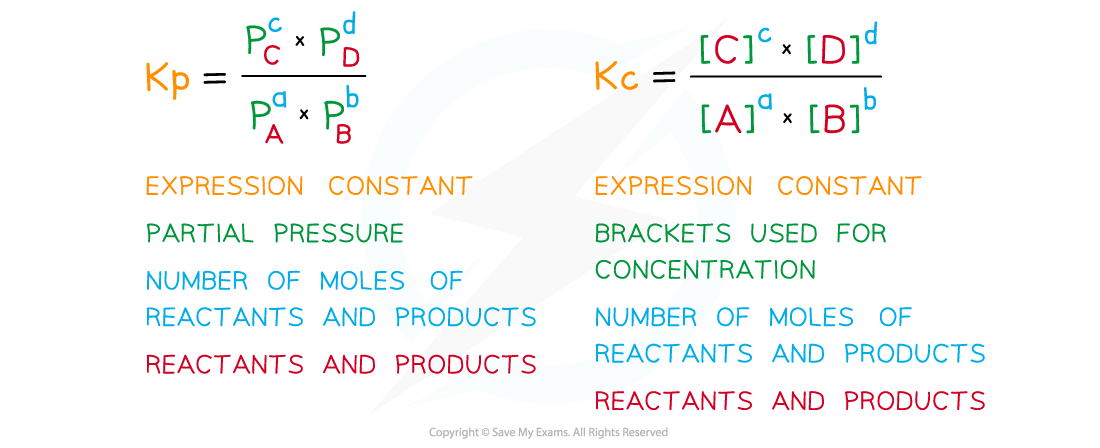
• Equilibrium expressions in terms of partial pressures are written similarly to those involving concentrations with a few differences:

Comparing K_p and K_c expressions 

The process of writing the expressions is similar, but there is a different presentation and different information required