Hess’s Law (Cambridge (CIE) AS Chemistry) : Revision Note
Hess Cycles
Hess’s Law states that:
"The total enthalpy change in a chemical reaction is independent of the route by which the chemical reaction takes place as long as the initial and final conditions are the same."
This means that whether the reaction takes place in one or two steps, the total enthalpy change of the reaction will still be the same
Illustration of Hess's Law
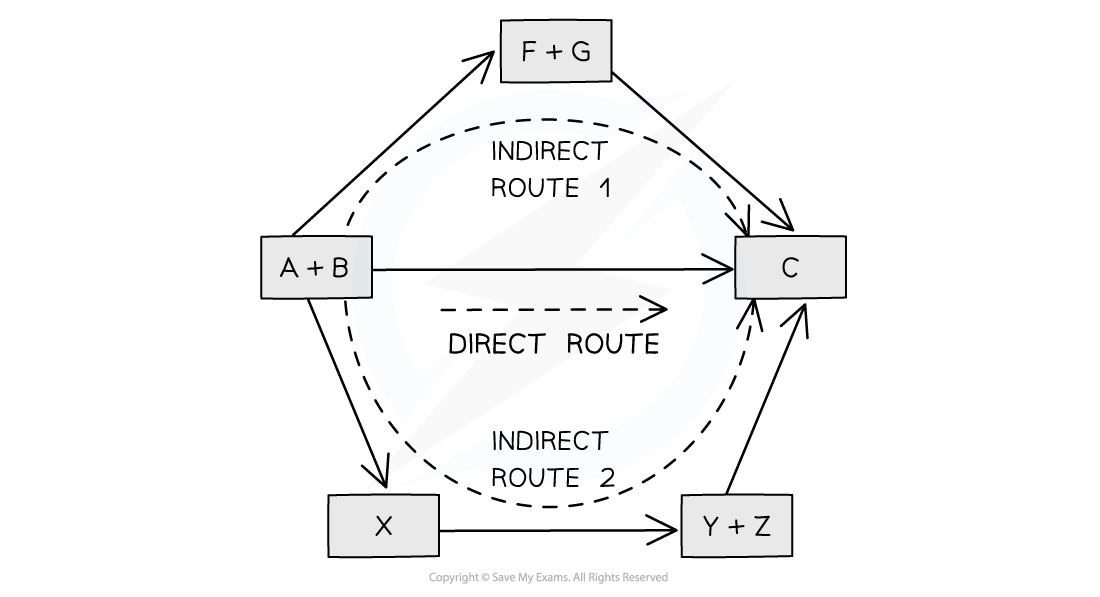
According to Hess’ Law, the enthalpy change of the direct route, going from reactants (A+B) to product (C), is equal to the enthalpy change of the indirect routes
Hess’ Law is used to calculate enthalpy changes which can’t be found experimentally using calorimetry, e.g.:
3C (s) + 4H2 (g) → C3H8(g)
ΔHf (propane) can’t be found experimentally as hydrogen and carbon don’t react under standard conditions
Calculating ΔHr from ΔHf using Hess’s Law energy cycles
The products can be directly formed from the elements = ΔH2 OR The products can be indirectly formed from the elements = ΔH1 + ΔHr
Applying Hess's Law
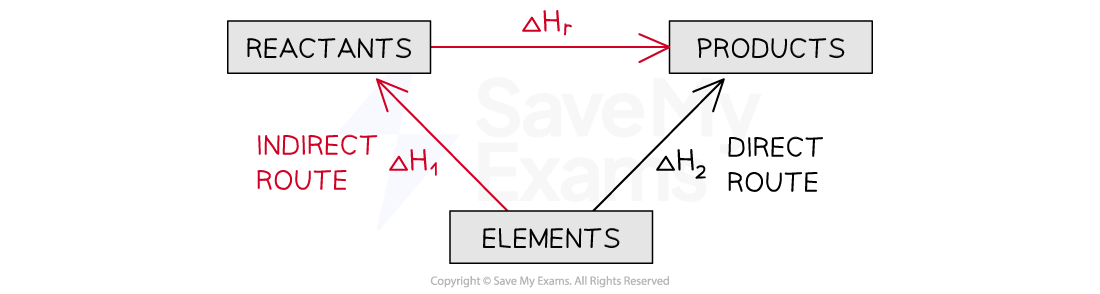
The enthalpy change from elements to products (direct route) is equal to the enthalpy change of elements forming reactants and then products (indirect route)
Equation
ΔH2 = ΔH1 + ΔHr
Therefore,
ΔHr = ΔH2 – ΔH1
Worked Example
Calculate ΔHr for the following reaction:
2NaHCO3 (s) → Na2CO3 (s) + CO2 (g) + H2O (l)
The table shows the standard enthalpy of formations, ΔHθf, relevant to this reaction.
Molecule | ΔHθf kJ mol-1 |
|---|---|
NaHCO3 (s) | –950.8 |
Na2CO3 (s) | –1130.7 |
CO2 (g) | –393.5 |
H2O (l) | –285.8 |
Answer
Step 1: Write the balanced equation at the top

Step 2: Draw the cycle with the elements at the bottom
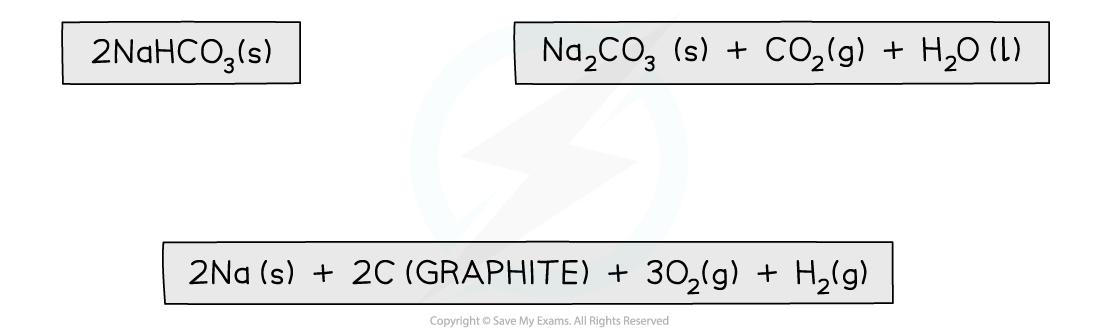
Step 3: Draw in all arrows, making sure they go in the correct directions. Write the standard enthalpy of formations
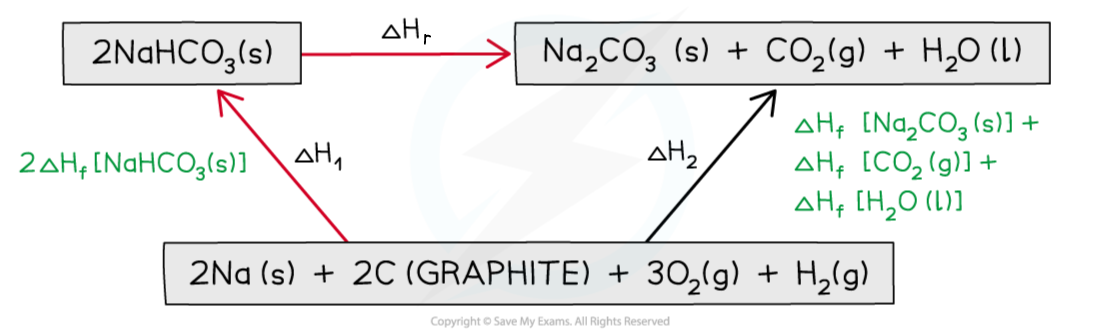
Step 4: Apply Hess’s Law:
ΔHr = ΔH2 – ΔH1
ΔHr = ( ΔHf [Na2CO3 (s)] + ΔHf [CO2 (g)] + ΔHf [H2O (l)] ) – 2ΔHf [NaHCO3 (s)]
ΔHr = ( (–1130.7) + (–393.5) + (–285.8) ) – ( 2 x –950.8)
ΔHr = +91.6 kJ mol-1
Calculating ΔHf from ΔHc using Hess’s Law energy cycles
The combustion products can be formed directly from elements to combustion products = ΔH1 OR The combustion products can be formed indirectly from elements to compounds to combustion products = ΔHf + ΔH2
Hess's Law and combustion enthalpies
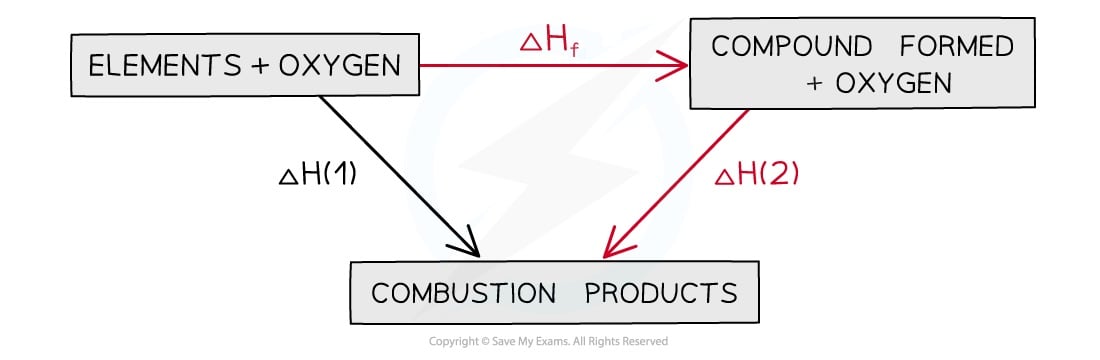
The enthalpy change going from elements to products (direct route) is equal to the enthalpy change of elements forming reactants and then products (indirect route)
Equation
ΔH1 = ΔHf + ΔH2
Therefore,
ΔHf = ΔH1 – ΔH2
Worked Example
Calculate, using the standard enthalpy change of combustion values given, the enthalpy of formation of ethane.
Reaction | ΔHc kJ mol-1 |
|---|---|
C (graphite) + O2 (g) → CO2 (g) | –393.5 |
H2 (g) + ½O2 (g) → H2O (l) | –285.8 |
C2H6 (g) + 3½O2 (g) → 2CO2 (g) + 3H2O (l) | –1559.7 |
Answer
Step 1: Write the equation for the enthalpy change of formation at the top and add oxygen on both sides
Step 2: Draw the cycle with the combustion products at the bottom
Step 3: Draw all arrows in the correct direction
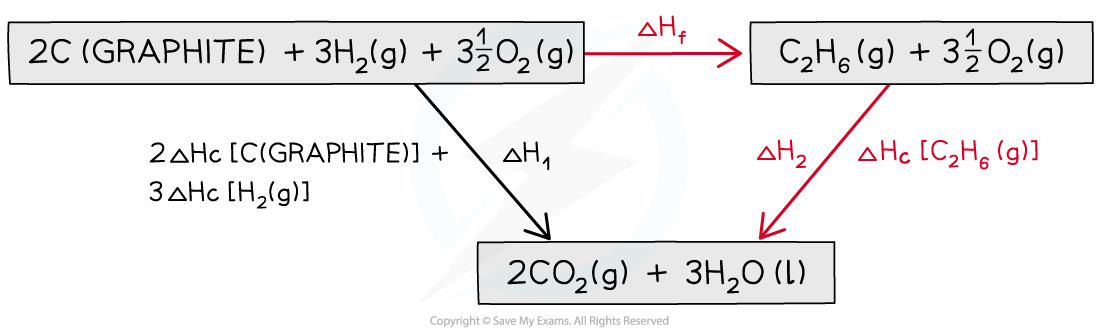
Step 4: Apply Hess’s Law:
ΔHf = ΔH1 – ΔH2
ΔHf = ( (2 x –393.5) + (3 x –285.8) ) – ( –1559.7)
ΔHf = –84.7 kJ mol-1
Calculating average bond energies using Hess's cycles
Bond energies cannot be found directly so enthalpy cycles are used to find the average bond energy
This can be done using enthalpy changes of atomisation and combustion or formation
The enthalpy change of atomisation (ΔHθat ) is the enthalpy change when one mole of gaseous atoms is formed from its elements under standard conditions.
E.g. ΔHθat [H2] relates to the equation:
½H2 (g) → H (g)
Worked Example
Calculate the average bond enthalpy of the C–H bond, using the relevant ΔHθf and ΔHθat values shown in the table.
| Energy kJ mol-1 |
|---|---|
ΔHθf [CH4 (g)] | –74.8 |
ΔHθat [½H2 (g)] | +218 |
ΔHθat [C (graphite)] | +717.7 |
Answer
Step 1: Write down the equation for the dissociation of methane at the top

Step 2: Write down the elements at the bottom
Step 3: Draw all arrows in the correct direction
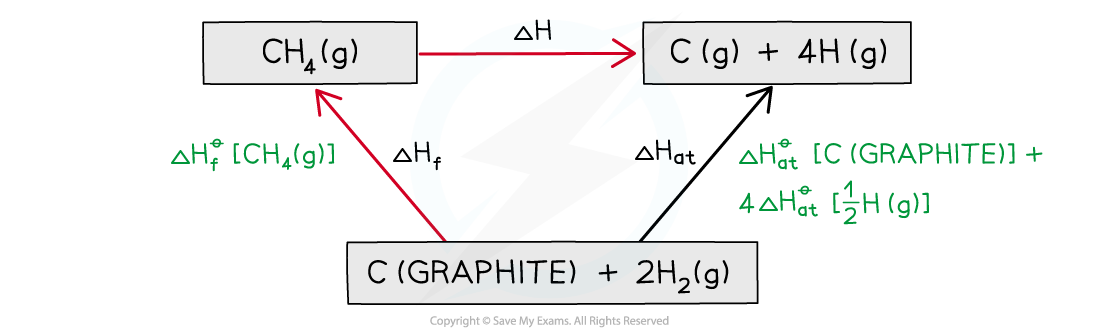
Step 4: Apply Hess’s Law:
ΔH = ΔHθat – ΔHf
ΔH = ( (+717.7) + (4 x 218) ) – ( –74.8)
ΔHf = +1664.5 kJ mol-1
Step 5: Calculate the bond energy for one C–H bond
There there are 4 C-H bonds in methane
Average bond enthalpy (C–H) =
Average bond enthalpy (C–H) = +416 kJ mol-1 (to 3 significant figures)
Examiner Tips and Tricks
Remember to take into account the number of moles of each reactant and product.
For example, there are two moles of NaHCO3 (s) so the ΔHf value is multiplied by 2.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
