Ideal Gases (CIE AS Chemistry)

Kinetic theory of gases

• The kinetic theory of gases states that molecules in gases are constantly moving
• The theory makes the following assumptions:
  • The gas molecules are moving very fast and randomly
  • The molecules hardly have any volume
  • The gas molecules do not attract or repel each other (no intermolecular forces)
  • No kinetic energy is lost when the gas molecules collide with each other (elastic collisions)
  • The temperature of the gas is related to the average kinetic energy of the molecules

• Gases that follow the kinetic theory of gases are called ideal gases
• However, in reality, gases do not fit this description exactly but may come very close and are called real gases

Ideal gases

• The volume that an ideal gas occupies depends on:
  • Its pressure
  • Its temperature
  • See section Changing gas volume on 1.4.1 Gas Pressure

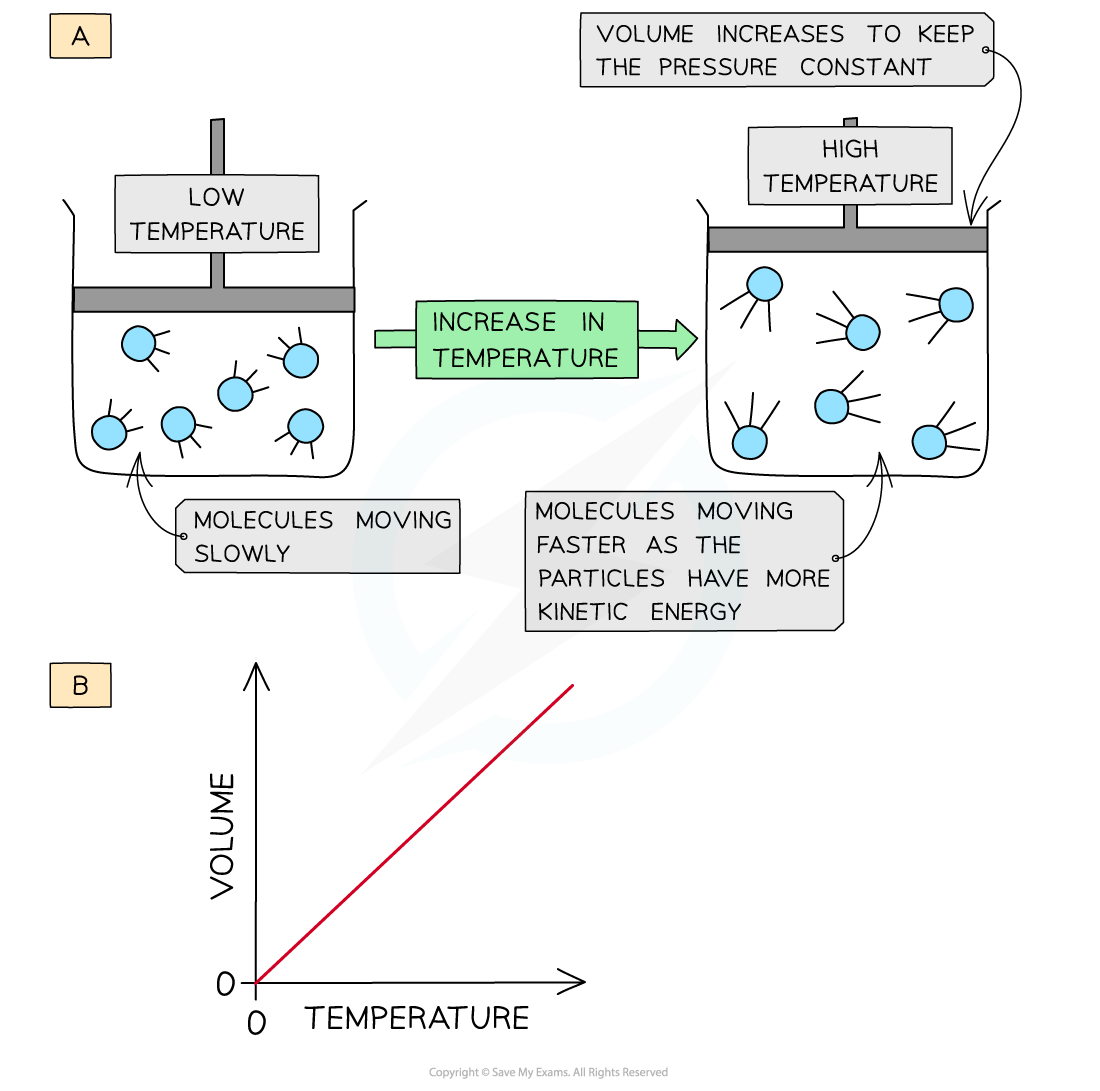
• When a gas is heated (at constant pressure) the particles gain more kinetic energy and undergo more frequent collisions with the container wall
• To keep the pressure constant, the molecules must get further apart and therefore the volume increases
• The volume is therefore directly proportional to the temperature (at constant pressure)

How the volume of a gas increases upon heating 

The volume of a gas increases upon heating to keep a constant pressure (a); volume is directly proportional to the temperature (b)

Limitations of the ideal gas law

• At very high pressures and low temperatures real gases do not obey the kinetic theory as under these conditions:
  • Molecules are close to each other
  • There are instantaneous dipole- induced dipole or permanent dipole- permanent dipole forces between the molecules
  • These attractive forces pull the molecules away from the container wall
  • The volume of the molecules is not negligible

• Real gases therefore do not obey the following kinetic theory assumptions at high temperatures and pressures:
  • There is zero attraction between molecules (due to attractive forces, the pressure is lower than expected for an ideal gas)
  • The volume of the gas molecules can be ignored (volume of the gas is smaller than expected for an ideal gas)

Ideal gas equation

• The ideal gas equation shows the relationship between pressure, volume, temperature and number of moles of gas of an ideal gas:

pV = nRT

   p = pressure (pascals, Pa)

   V = volume (m³)

   n = number of moles of gas (mol)

   R = gas constant (8.31 J K^-1 mol^-1)

   T = temperature (kelvin, K)

• The ideal gas equation can also be used to calculate the molar mass (M_r) of a gas