The rate of water loss from a plant shoot can be measured using a simple potometer, as shown in Figure 1.1 below. The amount of water taken up by the plant shoot can be measured using the scale on the pipette.
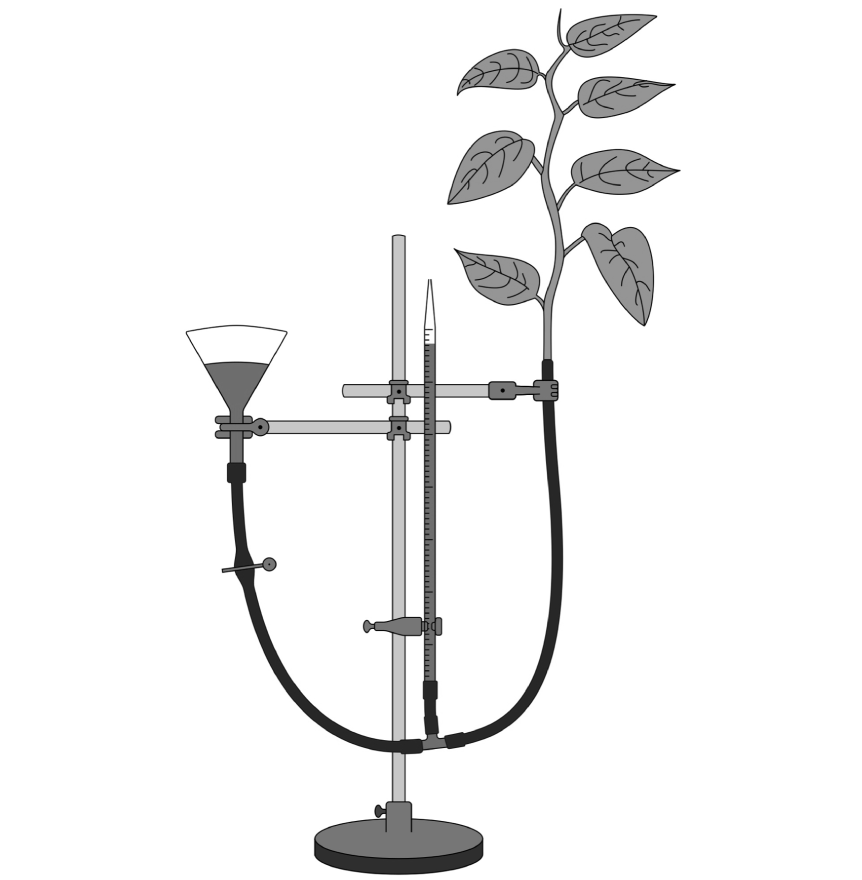
Figure 1.1
A student used this potometer apparatus and a lamp to investigate the effects of light intensity on the rate of water loss from the plant. They carried out the experiment at 5 different light intensities by varying the distance of the lamp from the plant.
Identify the dependent and independent variables in the experiment.
Describe how the student would measure the rate of water uptake at each light intensity.
Identify three variables that must be controlled.
Describe how the student could ensure that their results are reliable.
Did this page help you?










