AP®StatisticsCollege BoardStudy GuidesUnit 4: Probability, Random Variables & Probability DistributionsProbabilityEstimating Probability using Relative Frequency

Estimating Probability using Relative Frequency (College Board AP® Statistics)

Study Guide

Test yourself
Dan Finlay

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Probability language & notation

What are trials, outcomes and events?

Key term

Definition

Examples

Trial

An experiment that can be repeated

Rolling a biased dice and recording the number it lands on

Outcome

The result of a trial

The possible outcomes of rolling a standard six-sided dice are 1, 2, 3, 4, 5, and 6

Event

A collection of any number of outcomes, it could contain none, one or all of the outcomes

  • Rolling a number greater than 5

  • Rolling an even number

  • Rolling a number less than 7

  • Rolling a negative number

What is probability?

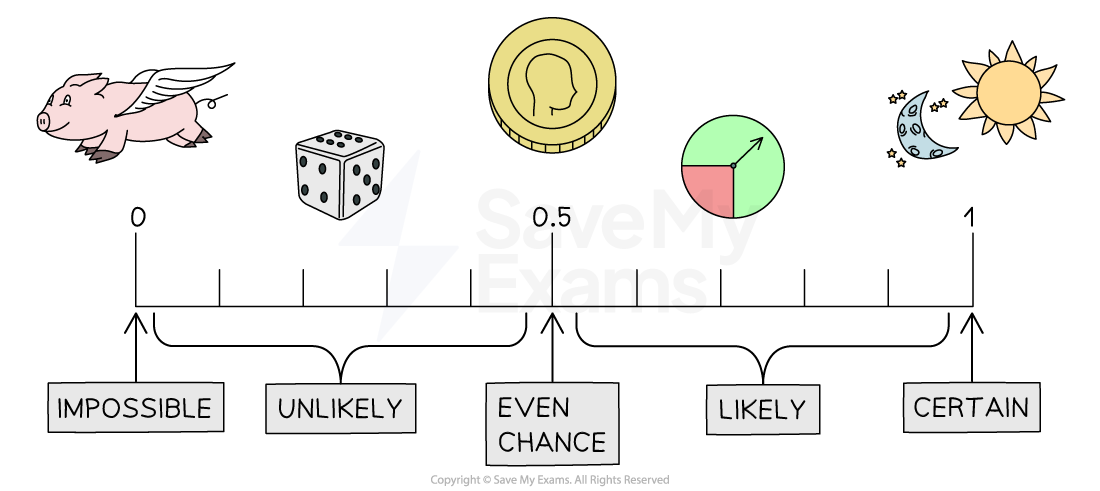
  • Probability is the likelihood of an event occurring

  • Probability is given as a numerical value between 0 and 1

    • 1 means the event will definitely occur

    • 0 means the event will definitely not occur

  • The probability of an event A is denoted as P open parentheses A close parentheses

    • 0 less or equal than P open parentheses A close parentheses less or equal than 1 for any event A

The probability scale goes from 0 to 1
The probability scale

Relative frequency & the law of large numbers

How can probabilities be estimated?

  • If the actual probability of an event is unknown then it can be estimated using trials

    • The trials can be real-life observations or simulations

  • The probability is estimated by dividing the number of times an outcome in the event occurred by the total number of trials

    • P open parentheses A close parentheses almost equal to fraction numerator number space of space times space an space outcome space in space event space A space occurred over denominator total space number space of space trials end fraction

    • This value is also called the relative frequency of the event or the empirical probability

Worked Example

A biased dice with faces labeled 1 to 6 is repeatedly rolled. The following table shows the number of times the dice landed on each face.

Label

1

2

3

4

5

6

Frequency

66

31

28

17

12

6

Find the relative frequency of the dice landing on a face labeled with a prime number.

Answer:

Identify the outcomes that are in the event

The event that the dice lands on a face labeled with a prime number contains the outcomes 2, 3 and 5

Find the number of times the dice landed on a face labeled with a prime number

31 plus 28 plus 12 equals 71

Find the total number of times the dice was rolled

66 plus 31 plus 28 plus 17 plus 12 plus 6 equals 160

Find the relative frequency by the number of times the dice landed on a face labeled with a prime number by the total number of times the dice was rolled

71 over 160 equals 0.44375

The relative frequency of the dice landing on a face labeled with a prime number is 0.44375

What is the law of large numbers?

  • The law of large numbers states that

    • as the number of trials increases

    • the relative frequency of an event tends to get closer to the actual probability of the event

  • One way to improve the estimate for a probability is to use more trials

Worked Example

Kai is investigating the probability that a surfer falls off their surfboard in Pe'ahi, Hawaii, during a big wave. Kai calculates the relative frequency for different numbers of attempts.

Number of attempts

10

100

200

500

Relative frequency

0.4

0.32

0.35

0.34

Which relative frequency is most likely to be the best estimate for the probability that a surfer falls off their surfboard during a big wave?

(A) 0.4

(B) 0.32

(C) 0.32

(D) 0.34

Answer:

The law of large numbers states that the relative frequency with the highest number of trials is most likely to be the best estimate for the probability

The correct answer is D

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Randomized Block & Matched Pairs DesignNext:Probabilities of Single Events
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Lucy Kirkham

    Author: Lucy Kirkham

    Expertise: Head of STEM

    Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels.Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all.