AP®StatisticsCollege BoardStudy GuidesUnit 4: Probability, Random Variables & Probability DistributionsProbabilityConditional Probability

Conditional Probability (College Board AP® Statistics)

Study Guide

Test yourself
Dan Finlay

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Conditional probability

What is a conditional probability?

  • A conditional probability is the probability that an event occurs given that another event has already occurred

  • The notation P open parentheses A vertical line B close parentheses is used to denote the probability of event Aoccurring given that B has occurred

    • Note that in general P open parentheses A vertical line B close parentheses not equal to P open parentheses B vertical line A close parentheses

  • A common use of conditional probability is when a sample is taken without replacement

    • If a unit is not replaced when sampled, then the total number of units decreases by 1 each time a unit is taken

Examiner Tips and Tricks

Look out for the phrase "given that" in an exam question. This phrase normally indicates that a conditional probability is needed.

Worked Example

There are 10 same-sized counters in a bag, 4 of them are red. A counter is chosen at random and it is not replaced. A second counter is then chosen at random.

What is the probability that the second counter is red, given that the first counter is red?

Answer:

Initially, there are 10 counters: 4 are red and 6 are not red

It is given that a red counter is chosen first and not replaced

This means there are now 9 counters remaining: 3 are red and 6 are not red

Find the probability that the second counter is red given that the first counter is red by dividing the number of remaining red counters by the total number of remaining counters

P open parentheses second space is space red vertical line first space is space red close parentheses equals 3 over 9

The probability can be simplified

Given that the first counter is red, the probability that the second counter is red is 1 third

How do I calculate a conditional probability for any two events?

  • To find the probability of event A given that event B has occurred

    • Restrict the sample space to just the outcomes in event B

      • Ignore any outcomes that are not in event B

    • Identify which of the remaining events are also in event A

    • Divide the probability of any of these outcomes occurring by the probability that event B occurs

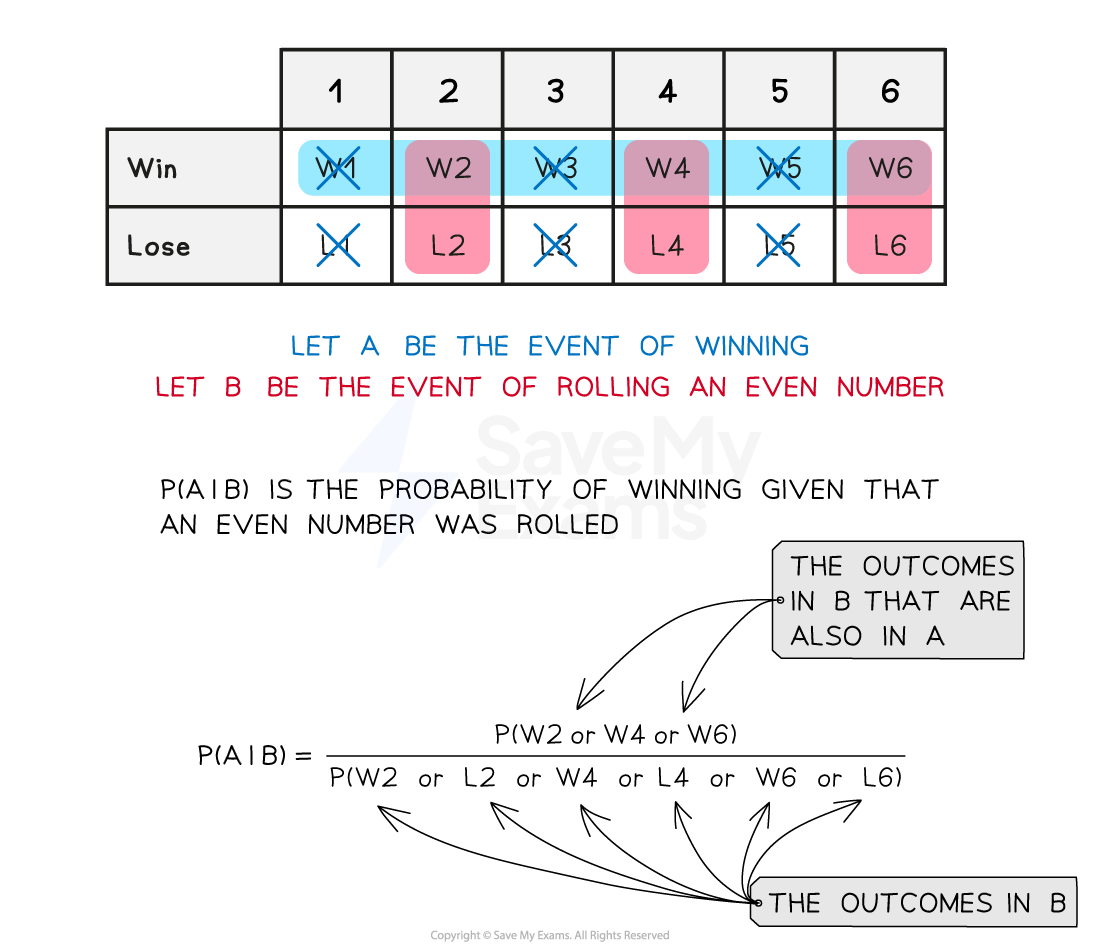
Table showing outcomes of a dice roll with winning and losing events, illustrating conditional probability. P(A|B) is P(W2 or W4 or W6) over P(W2, L2, W4, L4, W6, L6).
Example of finding a conditional probability by looking at the outcomes

  • The formula for conditional probability is P open parentheses A vertical line B close parentheses equals fraction numerator P open parentheses A intersection B close parentheses over denominator P open parentheses B close parentheses end fraction

    • This formula is given in the exam

Examiner Tips and Tricks

A common mistake that students make is using P open parentheses A close parentheses instead of P open parentheses A intersection B close parentheses on the numerator of the fraction. If B has already occurred then you essentially want to ignore any outcomes that are not in B.

Worked Example

In a school, a particular group of students are required to choose one math subject (Calculus or Statistics) and one language (French or Spanish).

17% of students chose Calculus and French, whereas 23% of students chose Calculus and Spanish. 25% of students chose Statistics and French and 35% of students chose Statistics and Spanish.

What is the probability that a randomly selected student chose Statistics, given that they also chose Spanish?

Answer:

The required probability is P open parentheses Statistics vertical line Spanish close parentheses

The conditional probability formula is P open parentheses Statistics vertical line Spanish close parentheses equals fraction numerator P open parentheses Statistics space and space Spanish close parentheses over denominator P open parentheses Spanish close parentheses end fraction

P open parentheses Statistics space and space Spanish close parentheses is given in the question but P open parentheses Spanish close parentheses is not

Find P open parentheses Spanish close parentheses by adding together the probabilities of the combinations involving Spanish

table row cell P open parentheses Spanish close parentheses end cell equals cell P open parentheses Calculus space and space Spanish close parentheses plus P open parentheses Statistics space and space Spanish close parentheses end cell row blank equals cell 0.23 plus 0.35 end cell row blank equals cell 0.58 end cell end table

Substitute the relevant probabilities into the conditional probability formula

table row cell P open parentheses Statistics vertical line Spanish close parentheses end cell equals cell fraction numerator P open parentheses Statistics space and space Spanish close parentheses over denominator P open parentheses Spanish close parentheses end fraction end cell row blank equals cell fraction numerator 0.35 over denominator 0.58 end fraction end cell row blank equals cell 35 over 58 end cell end table

Given that a randomly selected student chose Spanish, the probability that they also chose Statistics is 35 over 58 (roughly 0.603)

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Addition Rule & Mutually Exclusive EventsNext:Multiplication Rule & Independent Events
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Lucy Kirkham

    Author: Lucy Kirkham

    Expertise: Head of STEM

    Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels.Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all.