AP®StatisticsCollege BoardStudy GuidesUnit 4: Probability, Random Variables & Probability DistributionsProbabilityAddition Rule & Mutually Exclusive Events

Addition Rule & Mutually Exclusive Events (College Board AP® Statistics)

Study Guide

Test yourself
Dan Finlay

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Addition rule

What is the addition rule?

  • The addition rule is used to find the probability of the union of two events

  • To find the probability of A or B or both

    • Add together the probability of Aand the probability of B

    • Subtract the probability of A and B both occurring

      • This is because it has been counted twice (once for Aand once for B)

  • P open parentheses A union B close parentheses equals P open parentheses A close parentheses plus P open parentheses B close parentheses minus P open parentheses A intersection B close parentheses

    • This formula is given in the exam

  • The addition rule can be used to find the probability of the intersection of two events

    • P open parentheses A intersection B close parentheses equals P open parentheses A close parentheses plus P open parentheses B close parentheses minus P open parentheses A union B close parentheses

Worked Example

The owner of a company buys each employee a sandwich for lunch every day. One day, there are two options: peanut butter and jelly sandwiches or grilled cheese sandwiches.

64% of the employees like peanut butter and jelly sandwiches.

72% of the employees like grilled cheese sandwiches.

5% of the employees do not like either of the options.

Find the probability that a randomly selected employee likes both of the options.

Answer:

Let J be the event that the employee likes peanut butter and jelly sandwiches

Let C be the event that the employee likes grilled cheese sandwiches

Identify the probabilities

64% like peanut butter and jelly sandwiches and 72% like grilled cheese sandwiches

table row cell P open parentheses J close parentheses end cell equals cell 0.64 end cell row cell P open parentheses C close parentheses end cell equals cell 0.72 end cell end table

5% of employees do not like either of the options

table row cell P open parentheses J apostrophe intersection C apostrophe close parentheses end cell equals cell 0.05 end cell end table

This means that 95% of employees like at least one of the options

P open parentheses J union C close parentheses equals 0.95

Use the addition rule to find the probability that the employee likes both of the options

table row cell P open parentheses J union C close parentheses end cell equals cell P open parentheses J close parentheses plus P open parentheses C close parentheses minus P open parentheses J intersection C close parentheses end cell row cell 0.95 end cell equals cell 0.64 plus 0.72 minus P open parentheses J intersection C close parentheses end cell row cell P open parentheses J intersection C close parentheses end cell equals cell 0.41 end cell end table

The probability that a randomly selected employee likes both of the options is 0.41

Mutually exclusive events

What are mutually exclusive events?

  • Mutually exclusive events are events that contain no common outcomes

    • The events cannot happen at the same time

      • e.g. landing on a 5 and landing on an even number on the same dice roll are mutually exclusive events

      • e.g. landing on a 5 and landing on an odd number on the same dice roll are not mutually exclusive events

    • Mutually exclusive events are also called disjoint events

  • Any event and its complement are mutually exclusive

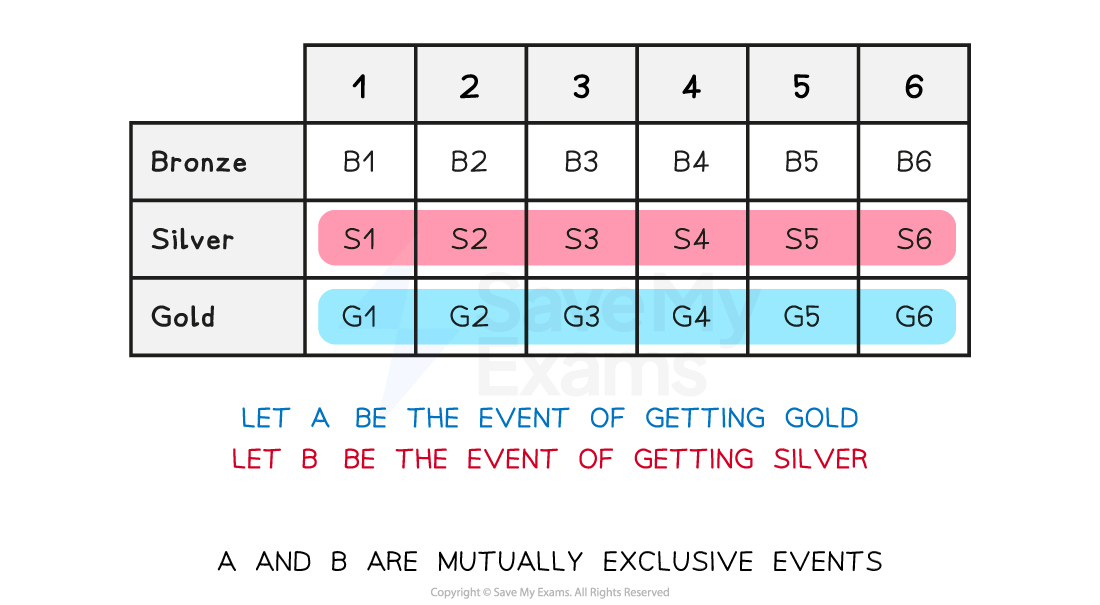
A table with rows labeled Bronze, Silver, and Gold, and columns numbered 1 to 6. Events A (getting gold) and B (getting silver) are highlighted as being mutually exclusive events.
Example of two mutually exclusive events

How can I check whether two events are mutually exclusive?

  • If Aand B are mutually exclusive events then P open parentheses A intersection B close parentheses equals 0

  • The addition rule for mutually exclusive events simplifies to P open parentheses A union B close parentheses equals P open parentheses A close parentheses plus P open parentheses B close parentheses

    • This can be extended to more than two events

      • e.g. if A, B and C are mutually exclusive events then P open parentheses A union B union C close parentheses equals P open parentheses A close parentheses plus P open parentheses B close parentheses plus P open parentheses C close parentheses

  • Too check whether A and B are mutually exclusive, check if one of the following equivalent statements is true:

    • P open parentheses A intersection B close parentheses equals 0

    • P open parentheses A union B close parentheses equals P open parentheses A close parentheses plus P open parentheses B close parentheses

How can I find probabilities involving mutually exclusive events?

  • If Aand B are mutually exclusive events then for any event E

    • P open parentheses E close parentheses equals P open parentheses E intersection A close parentheses plus P open parentheses E intersection B close parentheses

      • This is called the partition theorem

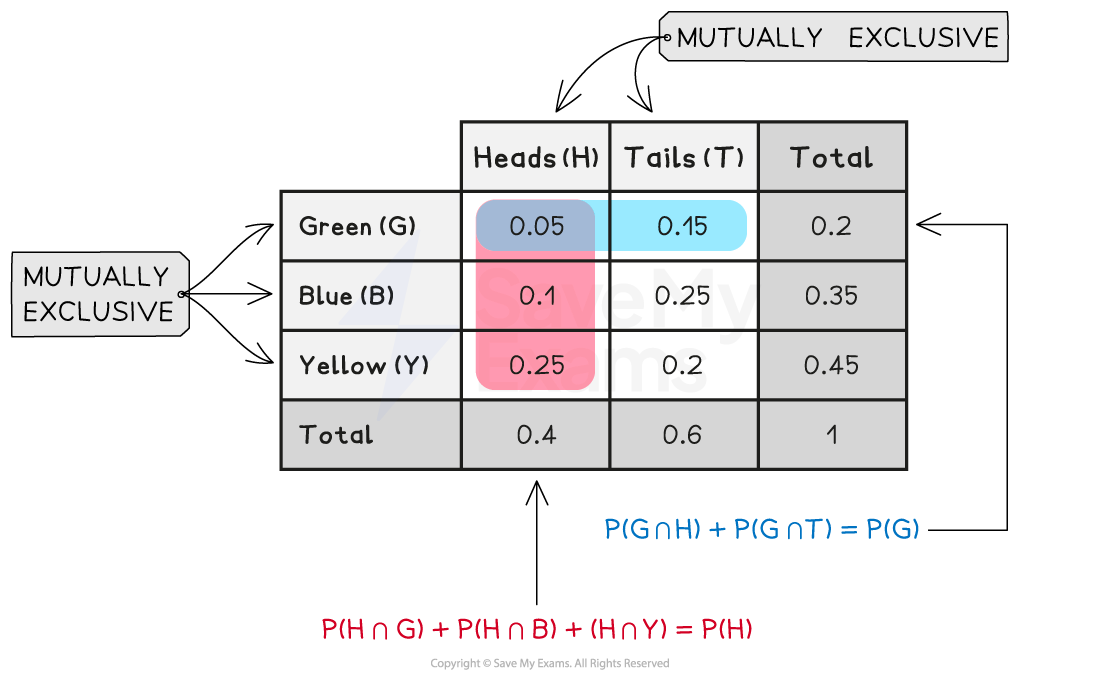
    • This formula is useful in exam questions especially when using a tree diagram or two-way tables

      • e.g. the probability of picking a green marble is equal to:

        • the probability of picking a green marble and a coin landing on heads

        • plus the probability of picking a green marble and a coin landing on tails

Probability table of outcomes with three rows of colors (green, blue, yellow) and two columns of the outcome of throwing a coin (heads and tails). It illustrates mutually exclusive events with labeled equations and sums.
Example of mutually exclusive events in a two-way table

Worked Example

In a high school, 15% of all the students wear glasses and 25% of all the students can write with their left hand. 35% of all the students wear glasses or can write with their left hand or both. A student is selected at random.

(a) Determine whether the events "the student wears glasses" and "the student can write with their left hand" are mutually exclusive. Explain your answer.

Answer:

Let G be the event that the student wears glasses

Let L be the event that the student can write with their left hand

Identify the probabilities

The 35% of students who wear glasses or can write with their left hand includes the students (if any) who wear glasses and can write with their left hand

table row cell P open parentheses G close parentheses end cell equals cell 0.15 end cell row cell P open parentheses L close parentheses end cell equals cell 0.25 end cell row cell P open parentheses G union L close parentheses end cell equals cell 0.35 end cell end table

If they are mutually exclusive then P open parentheses G union L close parentheses equals P open parentheses G close parentheses plus P open parentheses L close parentheses

Check to see if this formula works for these events

P open parentheses G close parentheses plus P open parentheses L close parentheses equals 0.4 P open parentheses G close parentheses plus P open parentheses L close parentheses not equal to P open parentheses G union L close parentheses

The events "the student wears glasses" and "the student can write with their left hand" are not mutually exclusive because P stretchy left parenthesis G union L stretchy right parenthesis not equal to P stretchy left parenthesis G stretchy right parenthesis plus P stretchy left parenthesis L stretchy right parenthesis

(b) Find the probability that the student wears glasses and cannot write with their left hand.

Answer:

The probability that is needed is P open parentheses G intersection L apostrophe close parentheses

Use the addition rule to find the probability that the student wears glasses and can write with their left hand

table row cell P open parentheses G union L close parentheses end cell equals cell P open parentheses G close parentheses plus P open parentheses L close parentheses minus P open parentheses G intersection L close parentheses end cell row cell 0.35 end cell equals cell 0.15 plus 0.25 minus P open parentheses G intersection L close parentheses end cell row cell P open parentheses G intersection L close parentheses end cell equals cell 0.05 end cell end table

A student can either write with their left hand or they cannot write with their left hand

Therefore the events L and L apostrophe are mutually exclusive so use the partition theorem P open parentheses G close parentheses equals P open parentheses G intersection L close parentheses plus P open parentheses G intersection L apostrophe close parentheses

table row cell 0.15 end cell equals cell 0.05 plus P open parentheses G intersection L apostrophe close parentheses end cell row cell P open parentheses G intersection L apostrophe close parentheses end cell equals cell 0.1 end cell end table

The probability that a student wears glasses and cannot write with their left hand is 0.1

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Introduction to Combined EventsNext:Conditional Probability
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Lucy Kirkham

    Author: Lucy Kirkham

    Expertise: Head of STEM

    Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels.Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all.