Mean & Standard Deviation of a Discrete Random Variable (College Board AP® Statistics)

Study Guide

Test yourself

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Mean of a discrete random variable

What is the mean of a discrete random variable?

The mean of a discrete random variable is the weighted average of the possible values based on their probabilities
- It is also known as the expected value
The mean of a random variable $X$ is denoted $μ_{X}$ or $E (X)$

How do I calculate the mean of a discrete random variable?

To calculate the mean of a discrete random variable $X$
- multiply each possible value of $x$ by its probability
- add these together
The formula is $μ_{X} = \sum x_{i} \cdot P (x_{i})$
- This is given in the exam
If the distribution is symmetrical then the mean is equal to the median of the values

How do I find the mean of a discrete random variable using a calculator?

To find the mean of a discrete random variable $X$ using a calculator
- type the values for $X$ in a list as if they were data values
- enter their probabilities as the frequencies
- find the summary statistics and identify the mean $\bar{x}$

Examiner Tips and Tricks

If you are asked to find the mean in a free response exam question then you must show your working. You can use your calculator to check your answer.

Worked Example

If a person chooses to donate to a charity, they can pay $1, $5 or $10.

Let $X$ represent the amount, in dollars, that a person pays to the charity when donating. The probability distribution of $X$ is shown in the table.

$x$	1	5	10
$P (x)$	0.6	0.3	0.1

What is the expected value of the amount that a person pays to the charity when donating?

Answer:

Use the formula $μ_{X} = \sum x_{i} \cdot P (x_{i})$

Multiply each value of $x$ by its probability then add the probabilities together

$\begin{array}{rcl} μ_{X} & = & 1 (0.6) + 5 (0.3) + 10 (0.1) \\ = & 3.1 \end{array}$

The expected value of the amount that a person pays to the charity when donating is $3.10

Standard deviation of a discrete random variable

What is the standard deviation of a discrete random variable?

The variance of a discrete random variable is the expected value of the squared differences between the values and the mean
The standard deviation of a discrete random variable is the positive square root of its variance
The standard deviation of a random variable $X$ is denoted $σ_{X}$

How do I calculate the standard deviation of a discrete random variable?

To calculate the standard deviation of a discrete random variable $X$
- subtract the mean from each value of $x$
- square them
- multiply each one by the probability of that value of $x$ occurring
- add these together
- take the positive square root
The formula is $σ_{X} = \sqrt{\sum {(x_{i} - μ_{X})}^{2} \cdot P (x_{i})}$
- This is given in the exam

How do I find the standard deviation of a discrete random variable using a calculator?

To find the standard deviation of a discrete random variable $X$ using a calculator
- type the values for $X$ in a list as if they were data values
- enter their probabilities as the frequencies
- find the summary statistics and identify the population standard deviation $σ$
  - the sample standard deviation, $s$ , should not exist in this case
  - $n = 1$ which means $n - 1 = 0$ and numbers cannot be divided by zero

Examiner Tips and Tricks

If you are asked to find the standard deviation in a free response exam question then you must show your working. You can use your calculator to check your answer.

Worked Example

The probability distribution of the discrete random variable $X$ is shown by the following graph.

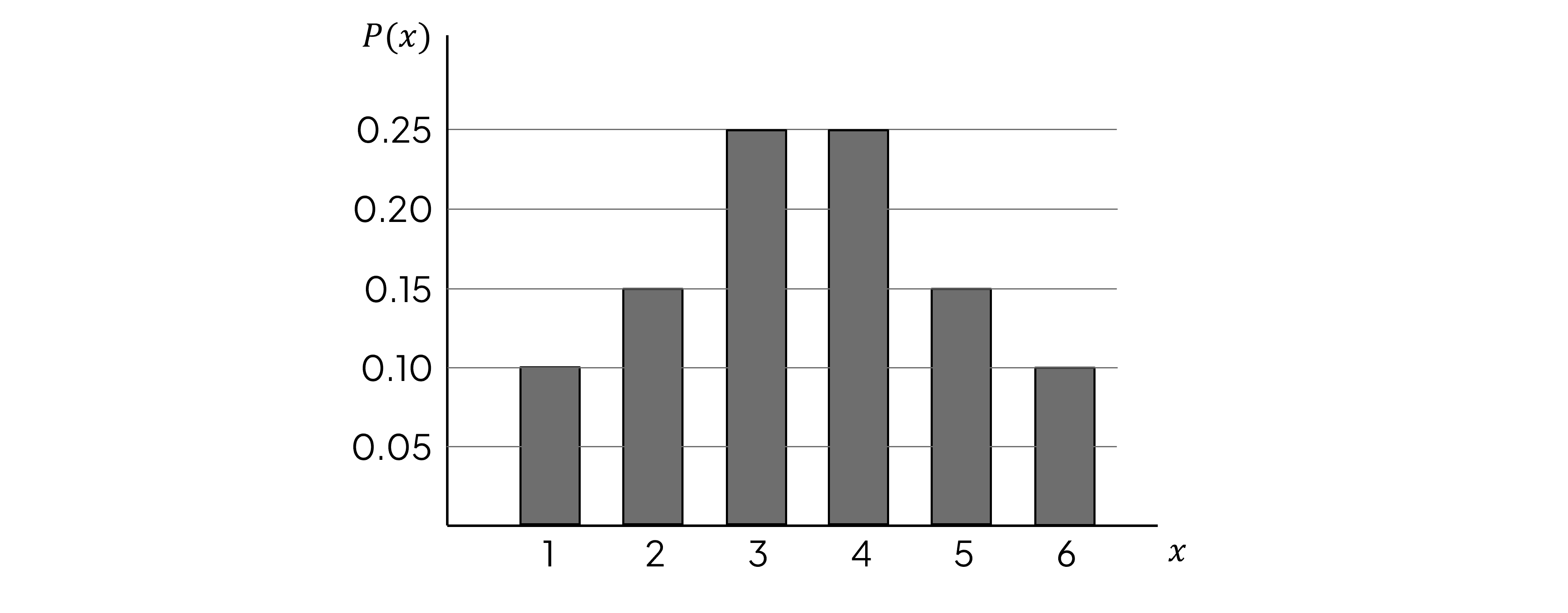
Bar graph showing probability distribution P(x) with x-values from 1 to 6. The probability for 1 and 6 is 0.1, the probability for 2 and 5 is 0.15 and the probability for 3 and 4 is 0.25

(a) Explain why the expected value of $X$ is 3.5.

Answer:

The distribution is symmetrical therefore the mean is equal to the median which is 3.5

(b) Calculate the standard deviation of $X$ .

Answer:

Use the formula $σ_{X} = \sqrt{\sum {(x_{i} - μ_{X})}^{2} \cdot P (x_{i})}$

Read the probabilities from the graph

Subtract 3.5 from each value of $x$ , square it and multiply it by its probability

Add together the probabilities and take the positive square root of the result

$\begin{array}{rcl} σ_{X} & = & \sqrt{{(1 - 3.5)}^{2} (0.1) + {(2 - 3.5)}^{2} (0.15) + {(3 - 3.5)}^{2} (0.25) + {(4 - 3.5)}^{2} (0.25) + {(5 - 3.5)}^{2} (0.15) + {(6 - 3.5)}^{2} (0.1)} \\ = & \sqrt{2.05} \\ = & 1.431 . . . \end{array}$

The standard deviation of $X$ is 1.43

Last updated: 13 August 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Cumulative Probability Distributions for Discrete Random VariablesNext:Linear Transformations of Random Variables

Mean & Standard Deviation of a Discrete Random Variable (College Board AP® Statistics)

Study Guide

Mean of a discrete random variable

What is the mean of a discrete random variable?

How do I calculate the mean of a discrete random variable?

How do I find the mean of a discrete random variable using a calculator?

Examiner Tips and Tricks

Worked Example

Standard deviation of a discrete random variable

What is the standard deviation of a discrete random variable?

How do I calculate the standard deviation of a discrete random variable?

How do I find the standard deviation of a discrete random variable using a calculator?

Examiner Tips and Tricks

Worked Example

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Dan Finlay

Author: Lucy Kirkham