Study GuidesExam QuestionsPast Papers
AP®StatisticsCollege BoardStudy GuidesUnits 6-9: InferenceIntroduction to InferenceTails on a Normal Distribution

Tails on a Normal Distribution (College Board AP® Statistics)

Study Guide

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Tails on a normal distribution

What are tails on a normal distribution?

  • Tails are the regions under the normal curve on the extreme left- or right-hand sides of the distribution

How do I find the most extreme P% of values from a normal distribution?

  • The most extreme P% of values in a normal distribution lie in the left-hand tail and the right-hand tail

    • Both tails are required

  • As the normal distribution is symmetric, this means

    • 1 half of P% of values lie in the left-hand tail

    • and 1 half of P% of values lie in the right-hand tail

A normal curve with peak at µ and symmetrical shaded areas under the curve on both sides labeled as 1/2 of P%, representing the extreme tails of the distribution.
The most extreme P% of values on a normal distribution

How do I find the middle Q% of values from a normal distribution?

  • To find the middle Q% of values from a normal distribution

    • it is easier to work out the percentage of values you do not want

      • 100% - Q%

    • then halve this value to give the percentage on each tail

      • fraction numerator 100 minus straight Q over denominator 2 end fraction%

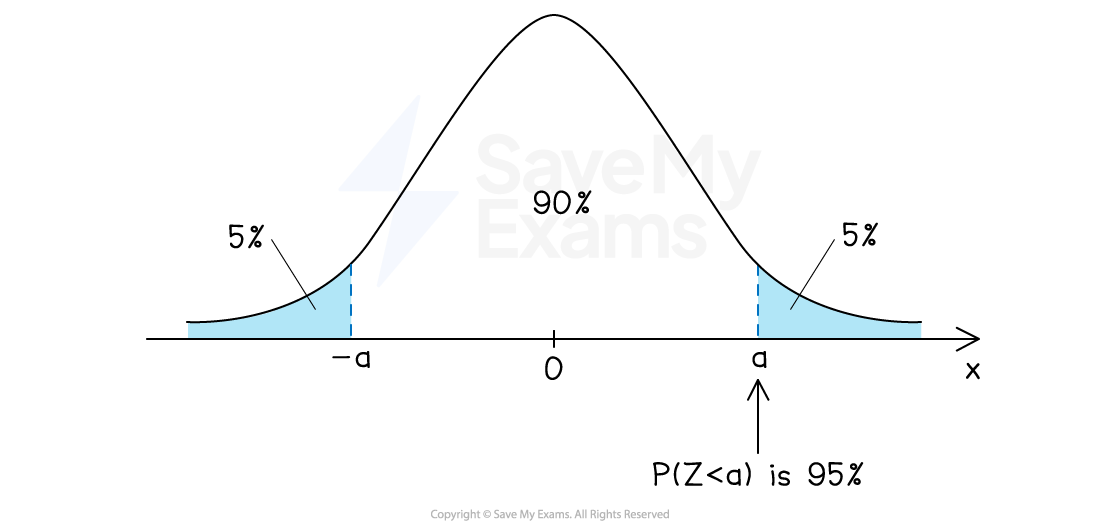
  • For example, the middle 90% of values has

    • 10% across both tails

    • so 5% on each tail

    • If the boundary values on the standard normal distribution are z equals plus-or-minus a then

      • there is a total of 5% + 90% = 95% to the left of z equals a

      • so P open parentheses Z less than a close parentheses equals 0.95

Standard normal curve showing 90% in the center and 5% in tails on either side, marked as -a and a. P(Z < a) is 95%.

Examiner Tips and Tricks

It is a common mistake to say the middle 90% of values has a standard normal boundary value, z equals a, that satisfies P open parentheses Z less than a close parentheses equals 0.9. The correct statement is P open parentheses Z less than a close parentheses equals 0.95.

How do I use the t-distribution tables to find boundary values?

  • The usual way to find boundary values for the middle 90% is to

    • let the positive boundary value be z equals a, then solve P open parentheses Z less than a close parentheses equals 0.95

      • This is an inverse normal calculation

      • i.e. find the probability closest to 0.95 in the normal tables

      • then read off the z-score

  • However, for certain common percentages that come up a lot (e.g the middle 50%, 90%, 95%, 99% etc of values) it is easier and more accurate to use

    • the very last row of the t-distribution table ('t-table')

      • called row infinity, infinity

    • as row infinity is a row of z-scores from the standard normal distribution

  • The percentage shown underneath row infinity is the middle percentage of values

    • not the percentage to the left

    • e.g. the middle 90% of values has a positive boundary z-score of 1.645 (from the t-tables)

      • This is more accurate than '1.64 or 1.65' from the normal tables

Examiner Tips and Tricks

You can, of course, use your calculator to do inverse normal calculations, but it is still worth knowing about the useful last row (row infinity) in the t-distribution tables!

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Biased & Unbiased EstimatorsNext:Introduction to Hypothesis Testing
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.