The t-distribution (College Board AP® Statistics)

t-distribution

What is the t-distribution?

• The t-distribution is a continuous probability distribution very similar to the normal distribution

• If a continuous random variable follows the t-distribution, then its shape will be:

  • symmetrical

  • mound-shaped (bell-shaped)

    • However, the tails will be 'thicker' for the t-distribution than for the normal distribution

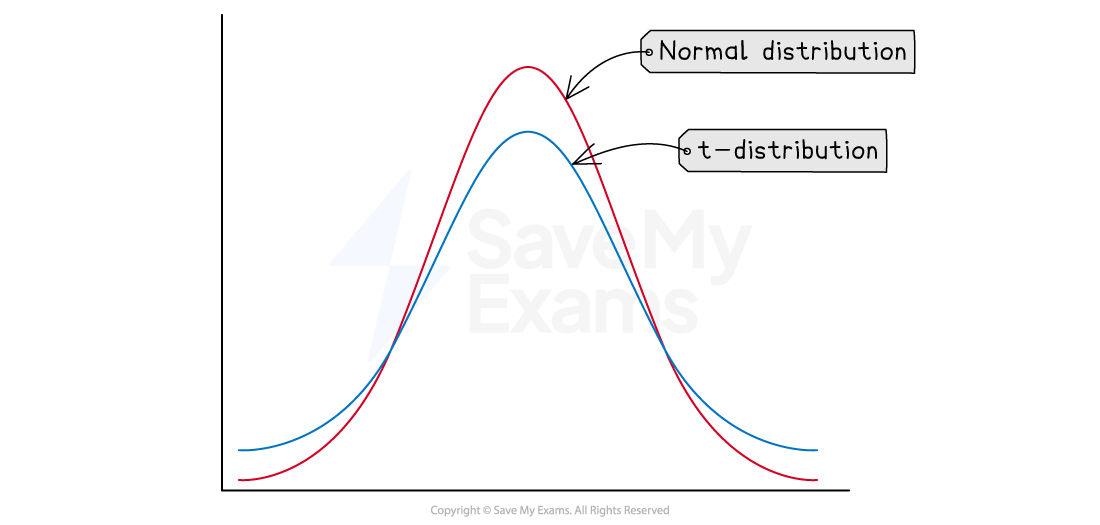
• Thicker tails means that there is a greater chance of getting more extreme values with a t-distribution than with a normal distribution

  • The t-distribution is more conservative than the normal distribution

• Degrees of freedom ('dof') is an additional parameter for the t-distribution curve

  • Increasing the degrees of freedom changes the shape of the curve, making the peak sharper and the tails thinner

  • The t-distribution curve approximates the standard normal curve, , more closely as the degrees of freedom increase

• The parameters of the t-distribution are similar to the standard normal distribution

  • The mean of the t-distribution is 0

  • The standard deviation of the t-distribution is greater than 1

    • but this gets closer to 1 as the degrees of freedom increase

When is the t-distribution used?

• The t-distribution is used, rather than the normal distribution, when:

  • the population standard deviation, , is unknown

  • and the population is approximately normally distributed

    • roughly symmetric

    • with no outliers

• If is unknown, the t-distribution can be used to

  • perform hypothesis tests for the population mean,

  • form confidence intervals for

• In practice, the t-distribution tends to be used more for smaller sample sizes () when is unknown

  • and the normal distribution is assumed for larger samples ()

    • as larger samples mean a higher degree of freedom

    • making the t-distribution approximate the standard normal distribution

  • however, in theory, the t-distribution is the correct distribution whenever is unknown, regardless of the sample size, !

How is a critical value found from the t-tables?

• The t-tables are given to you in the exam

• A critical value of t can be found from the t-tables

  • Find the row that corresponds to the number of degrees of freedom

  • Find the column that corresponds to the relevant significance level

  • The cell where these intersect contains the critical value of t

• The very last row of the t-distribution table is called row infinity,

  • Row infinity is a row of -scores from the standard normal distribution