Two-Way Tables & Relative Frequencies (College Board AP® Statistics)

Two-way tables

What is a two-way table?

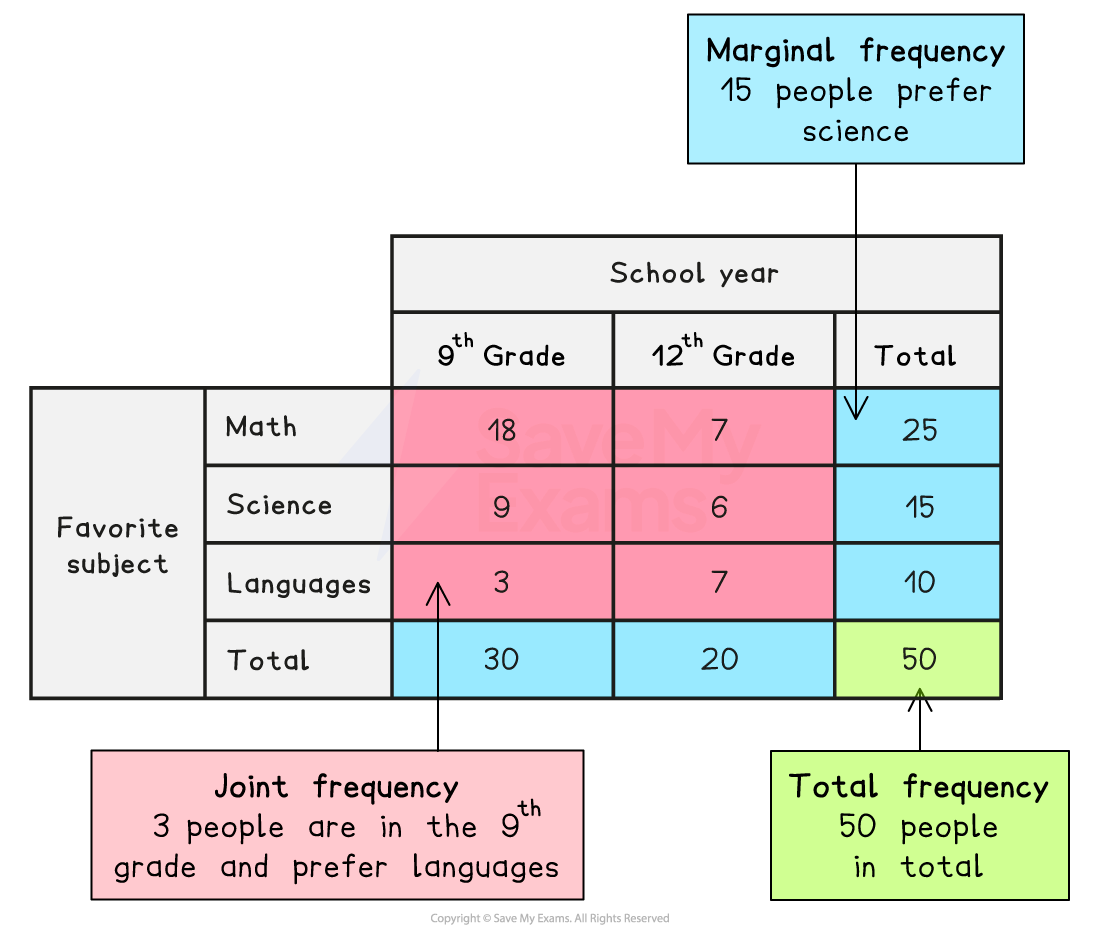
• A two-way table is used when there are two categorical variables

  • e.g. the school year and favorite subject of a random sample of students

• The rows represent one variable and the columns represent the other variable

• The number in a cell of a two-way table represents the frequency of the data, which satisfies the relevant values of both variables

  • This is called the cell frequency or the joint frequency

• The totals for each row and each column are usually included in a two-way table

  • These are called marginal frequencies

Joint, marginal & conditional relative frequencies

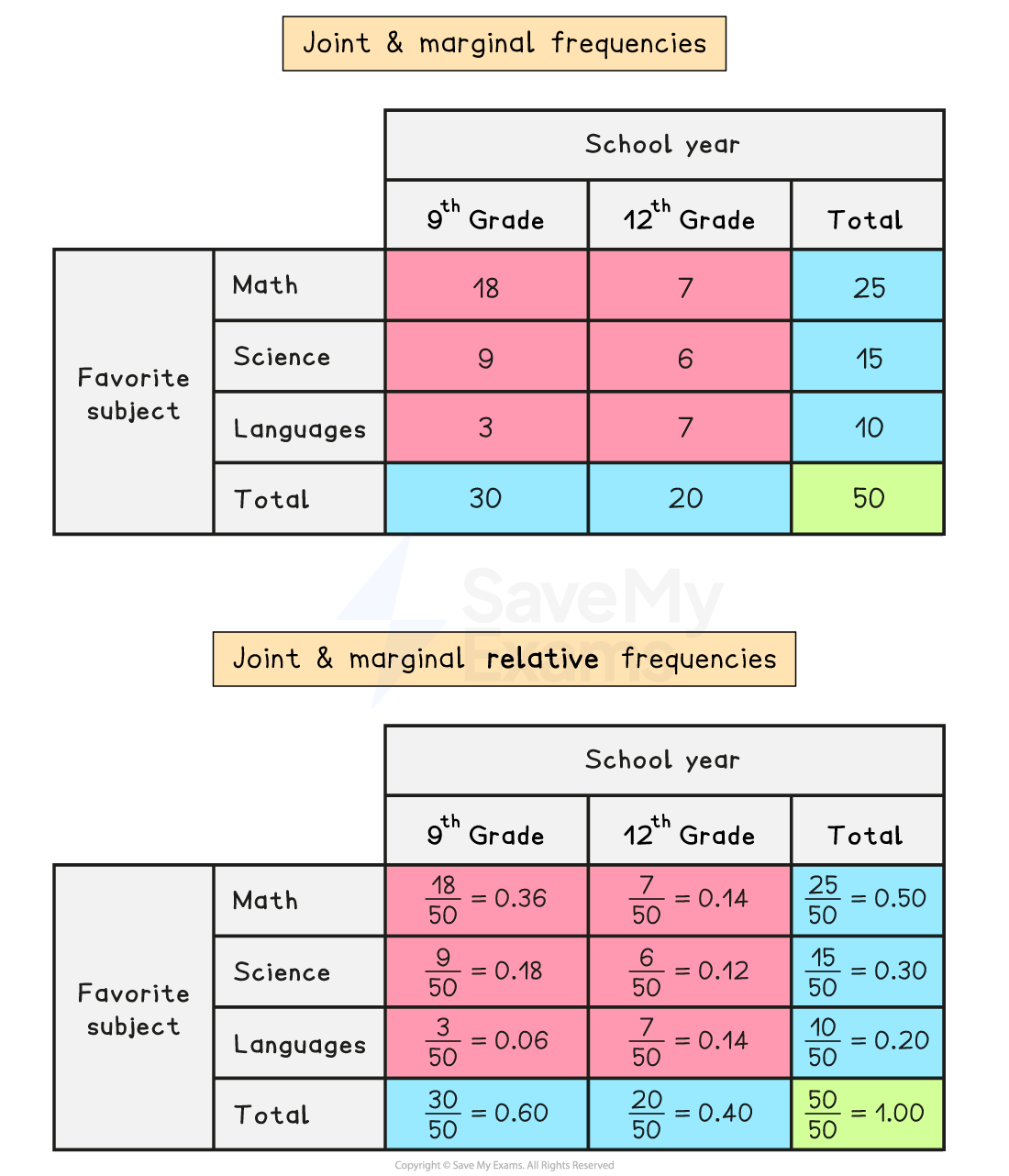
What are joint relative frequencies?

• The joint relative frequencies are the proportions of the total that belong to each cell

• To calculate a joint relative frequency for a cell

  • divide the joint (cell) frequency by the total frequency

    • e.g. divide the number of students in the 9^th grade who say math is their favorite subject by the total number of students

• If a two-way table is used to display joint relative frequencies then the total for the table is 1

What are marginal relative frequencies?

• The marginal relative frequencies are the proportions of the total that belong to each row or column

• To calculate a marginal relative frequency for a row or column

  • divide the marginal frequency by the total frequency

    • e.g. divide the number of students in the 9^th grade by the total number of students

• If a two-way table is used to display joint relative frequencies then each row or column will add up to the corresponding marginal relative frequency

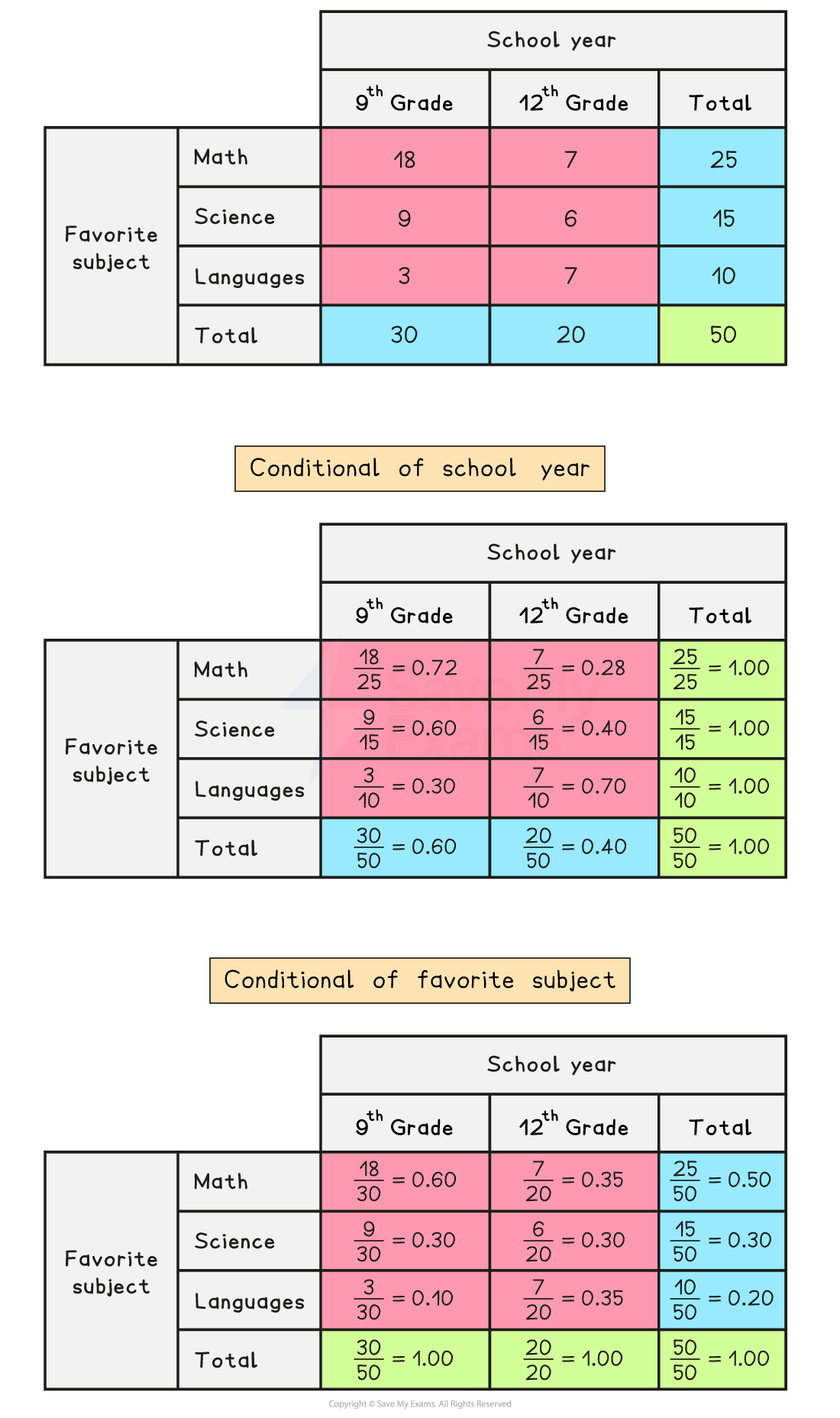
What are conditional relative frequencies?

• A conditional relative frequency is the proportion of the total of a row or column that belongs to that cell

  • e.g. the proportion of students in the 9^th grade who say math is their favorite subject is a conditional relative frequency

• To calculate a conditional relative frequency

  • divide the joint (cell) frequency by the relevant marginal frequency

    • e.g. divide the number of students in the 9^th grade who say math is their favorite subject by the total number of students in the 9^th grade

• If a two-way table is used to display conditional relative frequencies which are conditional of the row variable

  • then the conditional relative frequencies in each row will add up to 1

• If a two-way table is used to display conditional relative frequencies which are conditional of the column variable

  • then the conditional relative frequencies in each column will add up to 1