Study GuidesExam QuestionsPast Papers
AP®StatisticsCollege BoardStudy GuidesUnit 2: Exploring Two-Variable DataScatterplots & RegressionResidual Plots

Residual Plots (College Board AP® Statistics)

Study Guide

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Residual plots

What is a residual plot?

  • Recall that a residual is the vertical distance between a data point and the regression line

  • A residual plot is a graph that shows all the residuals from a scatterplot

    • The vertical axis shows the value of the residual

    • The horizontal axis shows the bold italic x-values

What is a residual plot used for?

  • When using the least-squares regression line, a residual plot gives a good indication as to whether the data points follow a linear model or not

    • If the residuals vary randomly from positive to negative then this suggests a linear model is a good fit for the data

    • If the residuals do not vary randomly (i.e. they follow a curve or form a pattern) then this suggests a linear model is not a good fit for the data

      • In this case, a non-linear (curved) model may be more appropriate

Worked Example

A scatterplot is shown below. The equation of the least-squares regression line is y with hat on top equals 2.4 plus 2.8 x, where y with hat on top is the predicted y-value. By constructing a residual plot, determine whether or not a linear model is appropriate for the data.

A scatterplot with points shown and a dashed regression line on a grid.

Answer:

First calculate the residuals (by finding the vertical distance of each data point above or below the regression line, y minus y with hat on top)

To find the y with hat on top-values from the regression line, it is more accurate to substitute the x-values into the equation of the line y with hat on top equals 2.4 plus 2.8 x, rather than read off their values from the graph

The residual at x equals 0 is 4 minus open parentheses 2.4 plus 2.8 cross times 0 close parentheses equals 1.6

The residual at x equals 1 is 2 minus open parentheses 2.4 plus 2.8 cross times 1 close parentheses equals negative 3.2 etc.

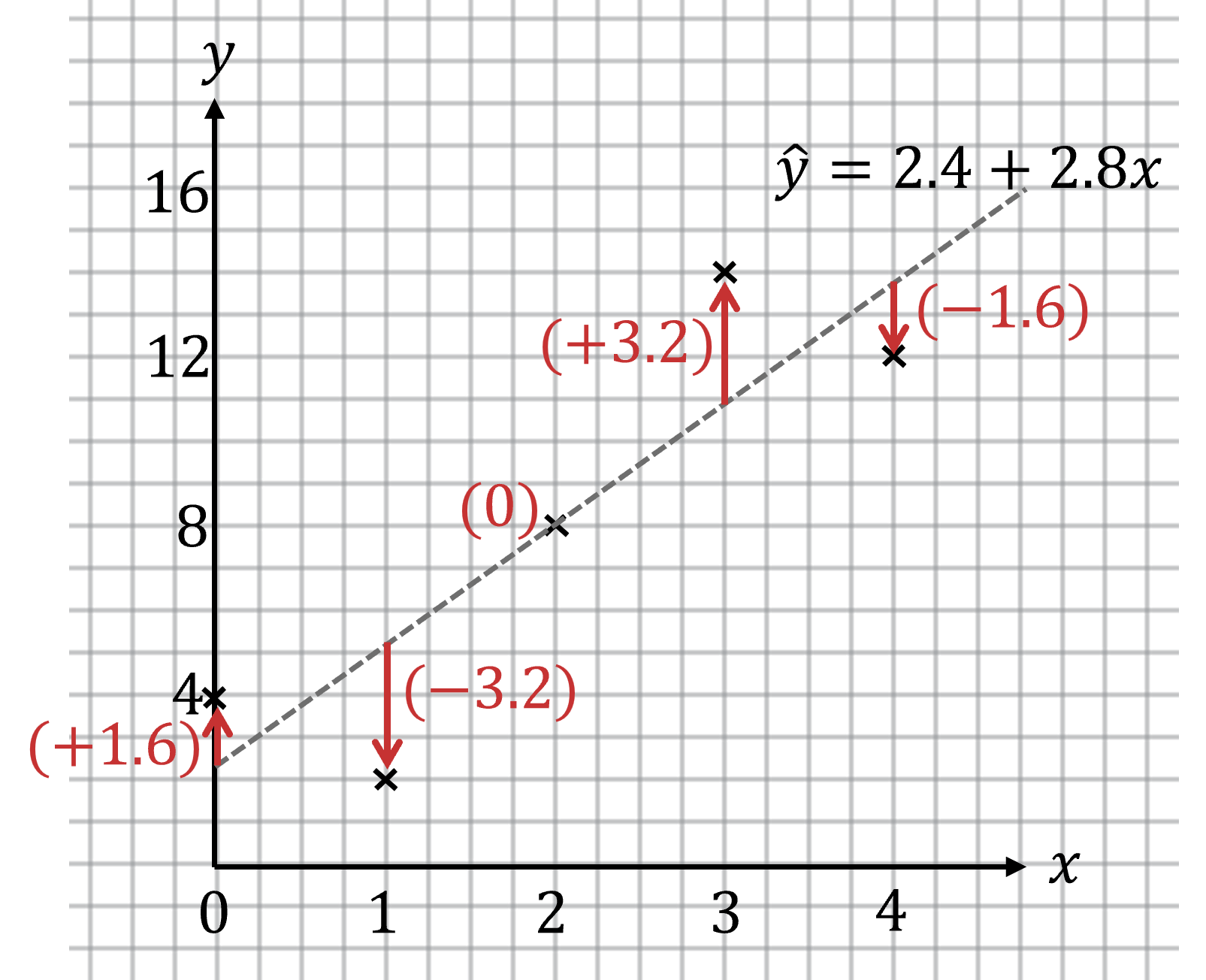
Scatterplot with a regression line with equation ŷ = 2.4 + 2.8x. Data points include he residuals: (+3.2), (+1.6), (–3.2), and (–1.6).

Then construct a residual plot by plotting the values of the residuals on the vertical axis and the x-values on the horizontal axis

A residual plot of residuals on the vertical axis against x-values on the horizontal axis.

If the residual plot shows that residuals vary randomly from positive to negative (without following a curve or a pattern), then a linear model is a good fit

The residual plot shows that residuals appear to vary randomly which suggests a linear model is appropriate for the data

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:The Least-Squares Regression LineNext:The Coefficient of Determination
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.