Association & Correlation Coefficients (College Board AP® Statistics)

Study Guide

Test yourself

Written by: Mark Curtis

Reviewed by: Dan Finlay

Association

What is an association?

An association between two variables means that the variables are related to each other in some particular way
- A change in one variable corresponds to a change in the other
It is possible for two variables to have no association
- A change in one variable does not correspond to a change in the other

What is the direction of an association?

If an association exists, it can have different directions:
- Positive association is when one variable increases, the other tends to increase
  - For example, as temperature increases, sales of cold drinks tend to increase
- Negative association is when one variable increases, the other tends to decrease
  - For example, increasing the age of a car tends to decrease its value

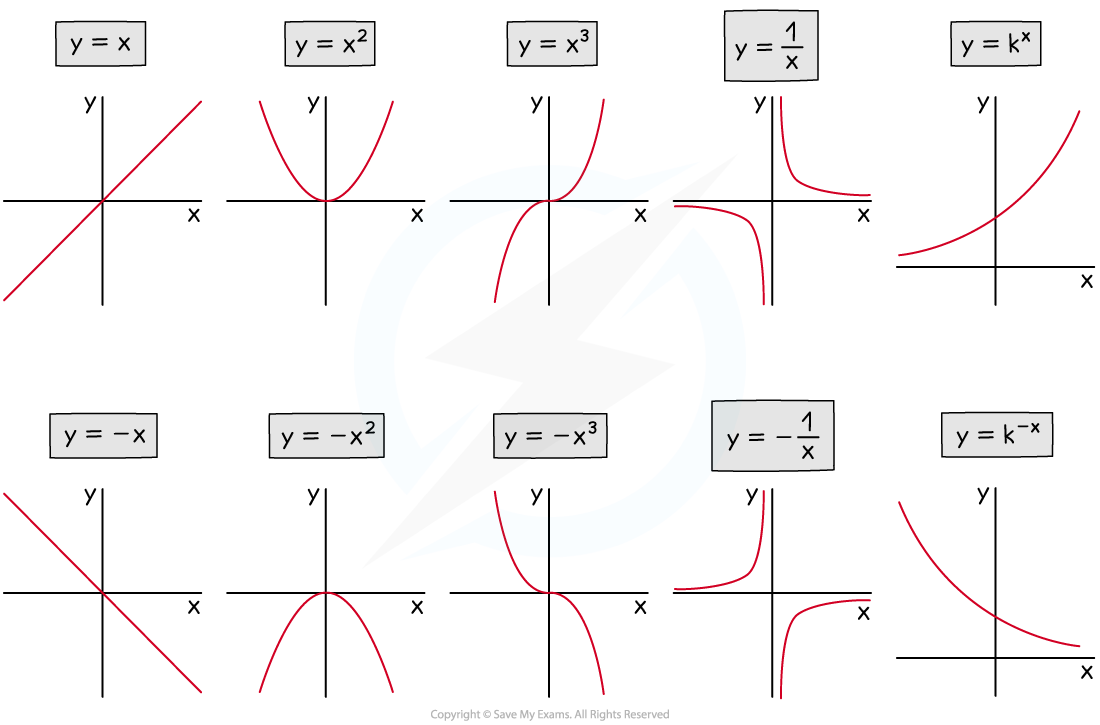
What is the form of an association?

Having a positive or negative association does not mean the association is linear (a straight line)
There are many different forms an association could take, for example:
- Linear forms follow straight lines
- Non-linear forms follow curved lines, including:
  - quadratics and cubics
  - reciprocals, e.g. $y = \frac{1}{x}$
  - exponentials, e.g. $y = 2^{x}$

Nine graphs show functions y = x, y = x², y = x³, y = 1/x, y = kˣ, y = -x, y = -x², y = -x³, and y = 1/x . — **Linear and non-linear forms of association**

What is the strength of an association?

The strength of an association is how well the data points on a scatterplot follow the form of the association
Strengths are described as either strong, moderate or weak
- The stronger the strength, the more closely data points follow the form
  - e.g. data points may show a 'weak quadratic' association

What are unusual features of a scatterplot?

Unusual features of a scatterplot include
- clusters
  - where data points appear to be in groups (clouds)
- outliers
  - data points that do not appear to fit the general pattern shown

Examiner Tips and Tricks

In the exam, if asked to describe the relationship shown on a scatterplot, you should comment in context on the direction (positive, negative, none), form (linear, non-linear) and strength (strong, moderate, weak) of an association, as well as any unusual features (clusters, outliers).

Worked Example

Describe the relationship shown between the hours spent on a phone per day and the hours spent on a computer per day for nine students in a class, shown on the scatterplot below.

Scatterplot showing hours spent on a computer per day (y-axis) versus hours spent on a phone per day (x-axis).

Answer:

You must comment on the strength, direction and form of the association seen

You must also comment on unusual features, in particular outliers and clusters

Remember to give your answer in context

The scatterplot reveals a strong, negative, roughly linear association between the hours spent on a phone per day and the hours spent on a computer per day for the nine students in the class

There are no significant outliers, though there is a slight clustering of points into two clusters (top left, between 1 and 3 hours on a phone per day, and bottom right, between 5 and 9 hours on a phone per day)

Correlation coefficients

What is correlation?

Correlation is a numerical measure of the direction and strength of a linear association between two variables

Five scatter plots illustrating different correlations: Strong Positive, Weak Positive, No Correlation, Weak Negative, and Strong Negative.

What is the correlation coefficient?

The correlation coefficient, $r$ , is a value between -1 and 1 where
- $r = 1$ means a perfect positive linear association
  - All points lie along the same straight line with a positive slope
- $r = 0$ means no linear association
- $r = - 1$ means a perfect negative linear association
  - All points lie along the same straight line with a negative slope
Values in between can be described as weak, moderate or strong
- e.g. $r = 0.9$ is a 'strong positive linear' association
  - Points appear to roughly follow a straight line with a positive slope

Nine scatter plots with correlation coefficients: six perfect (r = 1 or -1) showing diagonal lines, two moderate (r ≈ 0.7 and -0.4), and one (r = 0) showing no correlation.

What is the formula for the correlation coefficient?

For $n$ data points with coordinates $(x_{i}, y_{i})$ , the formula for the correlation coefficient is
- $r = \frac{1}{n - 1} \sum_{}^{} (\frac{x_{i} - \bar{x}}{s_{x}}) (\frac{y_{i} - \bar{y}}{s_{y}})$
- where $s_{x} = \sqrt{\frac{1}{n - 1} \sum_{}^{} {(x_{i} - \bar{x})}^{2}} = \sqrt{\frac{\sum_{}^{} {(x_{i} - \bar{x})}^{2}}{n - 1}}$ is the sample standard deviation of the $x$ -values
  - recall that $\bar{x} = \frac{1}{n} \sum_{}^{} x_{i} = \frac{\sum_{}^{} x_{i}}{n}$
- and where $s_{y} = \sqrt{\frac{1}{n - 1} \sum_{}^{} {(y_{i} - \bar{y})}^{2}} = \sqrt{\frac{\sum_{}^{} {(y_{i} - \bar{y})}^{2}}{n - 1}}$ is the sample standard deviation of the $y$ -values
  - and $\bar{y} = \frac{1}{n} \sum_{}^{} y_{i} = \frac{\sum_{}^{} y_{i}}{n}$
However, in practice, the correlation coefficient is found using technology
- e.g. using a calculator

Examiner Tips and Tricks

The formulas for $r$ , $s_{x}$ and $\bar{x}$ are given in the exam, but the formulas for $s_{y}$ and $\bar{y}$ are not (though they can easily be formed by looking at $s_{x}$ and $\bar{x}$ ).

What else do I need to know about correlation coefficients?

You need to know that correlation coefficients, $r$ , are
- always in the range $- 1 \leq r \leq 1$
- only measure strengths of linear relationships
  - so $r = 0$ has no linear association, but may have a non-linear (curved) association
- independent of units
  - changing the units of the $x$ and $y$ variables does not affect $r$
- affected by outliers
- not affected by swapping the axes
  - i.e. plotting $y$ values on the $x$ axis and vice versa

What does the phrase "correlation does not imply causation" mean?

If two variables appear to correlate, it does not mean that one variable causes changes in the other variable
For example, each day you record the height of a sunflower and the weight of a puppy
- As the height of the sunflower increases, the weight of the puppy increases
  - This shows a positive correlation
- But you cannot claim that:
  - 'increasing the heights of sunflowers causes puppies to weigh more'
  - or 'heavier puppies lead to taller sunflowers'!
- Both variables are actually increasing separately due to a third variable
  - In this case, time

Last updated: 28 August 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:ScatterplotsNext:Interpolation & Extrapolation using Linear Models

Association & Correlation Coefficients (College Board AP® Statistics)

Study Guide

Association

What is an association?

What is the direction of an association?

What is the form of an association?

What is the strength of an association?

What are unusual features of a scatterplot?

Examiner Tips and Tricks

Worked Example

Correlation coefficients

What is correlation?

What is the correlation coefficient?

What is the formula for the correlation coefficient?

Examiner Tips and Tricks

What else do I need to know about correlation coefficients?

What does the phrase "correlation does not imply causation" mean?

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Mark Curtis

Author: Dan Finlay