Properties of Normal Distributions (College Board AP® Statistics): Study Guide
Continuous random variables
What is a continuous random variable?
A continuous random variable (CRV) is a random variable whose value lies within one or more intervals on a number line
The number of values that a CRV could be, within a given interval, are infinite
e.g. the weight of a squirrel is a continuous random variable, a squirrel selected at random could take on any value within the given interval
In some cases it can be easy to confuse continuous and discrete variables
e.g. foot length is a continuous variable, as it can be measured to any specified degree of accuracy
but shoe size is a discrete variable as it can be counted (4, 5, 6, etc.)
What is a continuous probability distribution?
A continuous probability distribution describes the probabilities of the occurrences of each possible outcome associated with a continuous random variable
As there are an infinite number of possible values for a continuous random variable within a given interval
the probability that it assumes one specific value is 0
i.e. for a value
in the given interval,
Instead we talk about the probability of
being within a certain range
A continuous probability distribution can be represented by a continuous graph,
, called a probability density function
the values for
lie along the horizontal axis
and the probability density is given on the vertical axis
The area under the graph between the points
and
is equal to
The total area under the graph equals 1
As
for any value
, it does not matter if we use strict or weak inequalities
for any value of
Properties of normal distributions
What is a normal distribution?
A normal distribution is a continuous probability distribution
If a continuous random variable follows a normal distribution, then its shape will be:
symmetrical
mound-shaped (bell-shaped)
If
follows a normal distribution then
is the mean
is the standard deviation
What are the important properties of a normal distribution?
The normal distribution is symmetrical about
Mean = Median = Mode =
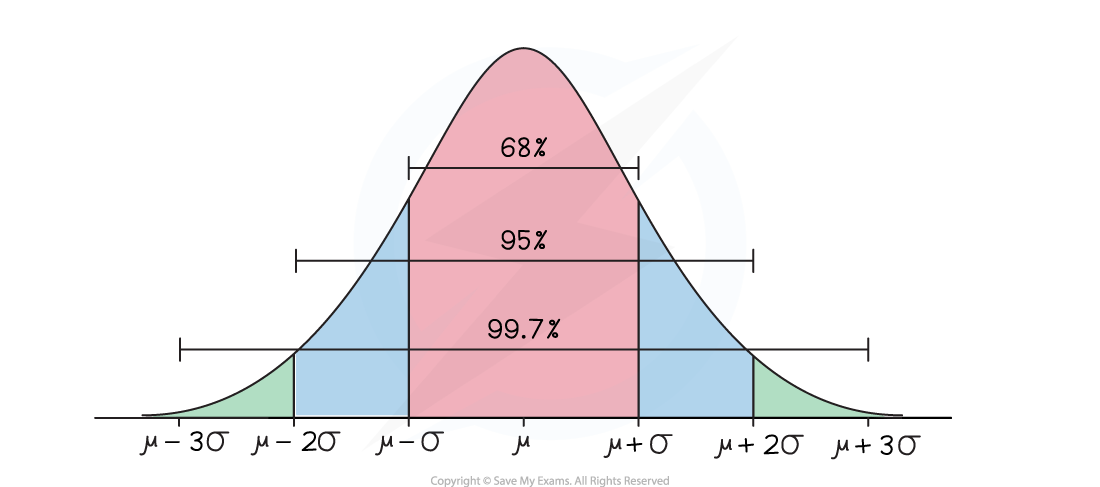
The empirical rules state that the data in a normal distribution is distributed such that (approximately):
68% of the data lies within one standard deviation of the mean
95% of the data lies within two standard deviations of the mean
99.7% lies within three standard deviations of the mean
Worked Example
The distribution of the travel range of adult female grizzly bears follows approximately a normal distribution. Based on a very large sample, it was found that 16 percent of the bears had a travel range of less than 6.9 miles and 84 percent of the bears had a travel range of less than 8.1 miles. What are the mean and standard deviation of the distribution of the travel ranges of the adult female grizzly bears?
Answer:
Subtract the percentage of bears that have a travel range of less than 8.1 miles from 100% to find the percentage of bears that have a travel range of greater than 8.1 miles
100% - 84% = 16%
It can be useful to sketch a diagram of the distribution
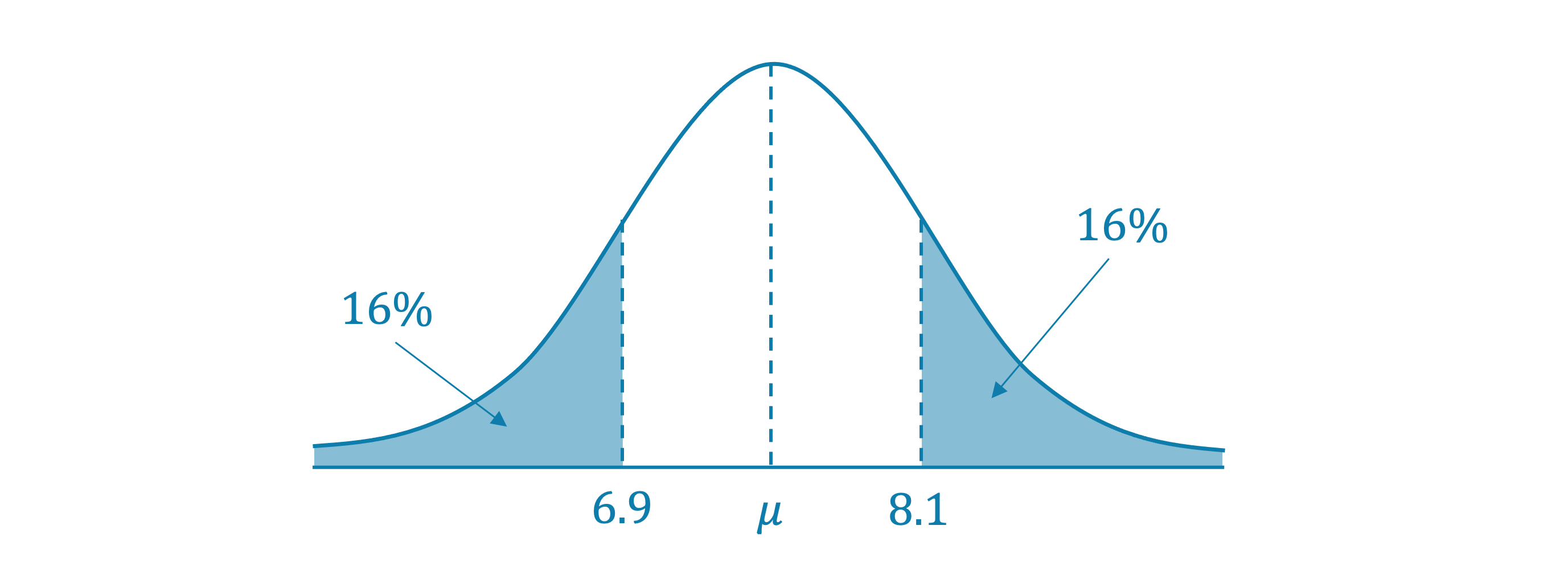
Because the distribution is symmetrical, the mean of the distribution will be halfway between the two values
Find the percentage of bears that have a travel range of between 6.9 miles and 84 miles
84% - 16% = 68%
Approximately 68% of the data of a normal distribution lies within one standard deviation of the mean
Each of the values 6.9 and 8.1 are one standard deviation either side of the mean, you can therefore find the value of the standard deviation by dividing the difference between the two values by two
The distribution of the travel ranges of the adult female grizzly bears has a mean of 7.5 miles with standard deviation 0.6 miles
What can be modeled using a normal distribution?
A lot of real-life continuous variables can be modeled by a normal distribution if:
the population is large enough
and the variable is roughly symmetrical with one mode
For a normal distribution, the continuous random variable
can take any real value
However, values far from the mean (more than 4 standard deviations away) have a probability density of practically zero
This allows us to model variables that are not defined for all real values, e.g. height and weight
What cannot be modeled using a normal distribution?
Variables which have more than one mode or no mode
e.g. the number given by a random number generator
Variables which are not symmetrical
e.g. how long a human lives for
Variables in which acceptable ranges of values (within 3 standard deviations of the mean) become negative when they are meant to be positive
e.g. length modeled by a normal distribution with mean 10 cm and standard deviation 8 cm
3 standard deviations below the mean would be
and a length cannot be negative
Worked Example
The random variable represents the speeds (mph) of a certain species of cheetahs when they run. The variable is modeled using a mean of 40 mph and a standard deviation of 10 mph.
State the two assumptions that have been made about the shape of the distribution of cheetah speeds in order to use this.
Answer:
We assume that the distribution of cheetah speeds is symmetrical and mound-shaped

You've read 0 of your 5 free study guides this week
Unlock more, it's free!
Did this page help you?