Inverse Normal Calculations (College Board AP® Statistics)

Study Guide

Test yourself

Written by: Naomi C

Reviewed by: Dan Finlay

Inverse normal calculations

Given the value P(X < a) how do I find the value of a using the standard normal table?

The proportion of a distribution of a variable $X$ that lies below a given value is the area under the curve to the left of the given value
- This is also the probability that the variable lies below this value
- $P (X < a) = p$

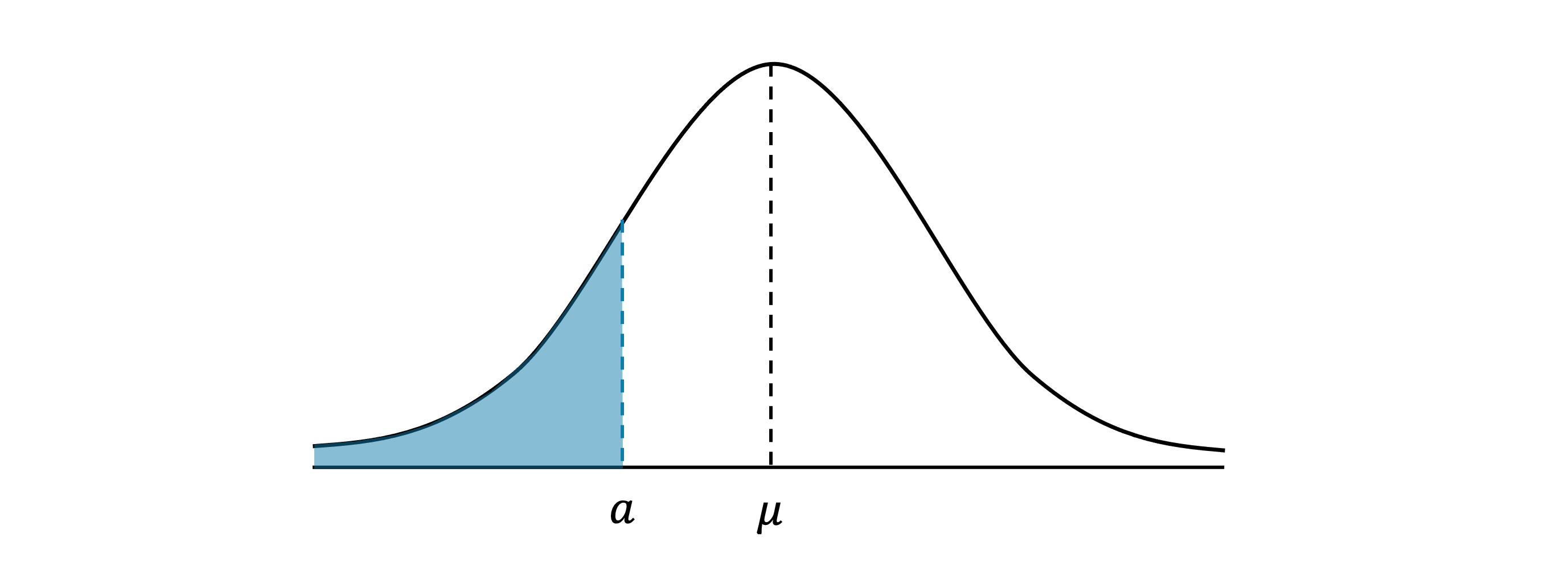
A normal distribution curve with mean μ and shaded area to the left of a vertical dashed line at a. The mean is labeled μ and point a is labeled a. — **Normal distribution with proportion of distribution less than a shaded**

$P (X < a) = P (Z < z)$
- where $z$ is the $z$ -score of the value $a$
If you are given the proportion (or probability) and want to work out the value of $a$ :
- find the cell in the standard normal table that is
  - equal to the proportion
  - or the highest value that is less than the proportion
- identify the $z$ -score by listing the relevant row and column
- convert the $z$ -score back into an actual value

Given the value of P(X < a) how do I find the value of a using a calculator?

Your calculator will have a function called Inverse Normal Distribution
- Some calculators call this InvN
Given that $P (X < a) = p$ you will need to enter:
- The proportion (or probability), $p$
  - This is the area of the distribution to the left of $a$
- The mean, $μ$
- The standard deviation, $σ$
Some calculators might ask for the tail
- For $P (X < a)$ this is the left tail

Examiner Tips and Tricks

Always check your answer makes sense!

If $P (X < a)$ is less than 0.5 then $a$ should be smaller than the mean,
If $P (X < a)$ is more than 0.5 then $a$ should be bigger than the mean.

A sketch will help you see this.

Given the value of P(X > b) how do I find the value of a using the standard normal table?

The proportion of a a distribution of a variable $X$ that lies above a given value is the area under the curve to the right of the given value
- This is also the probability that the variable lies above this value
- $P (X > b) = p$

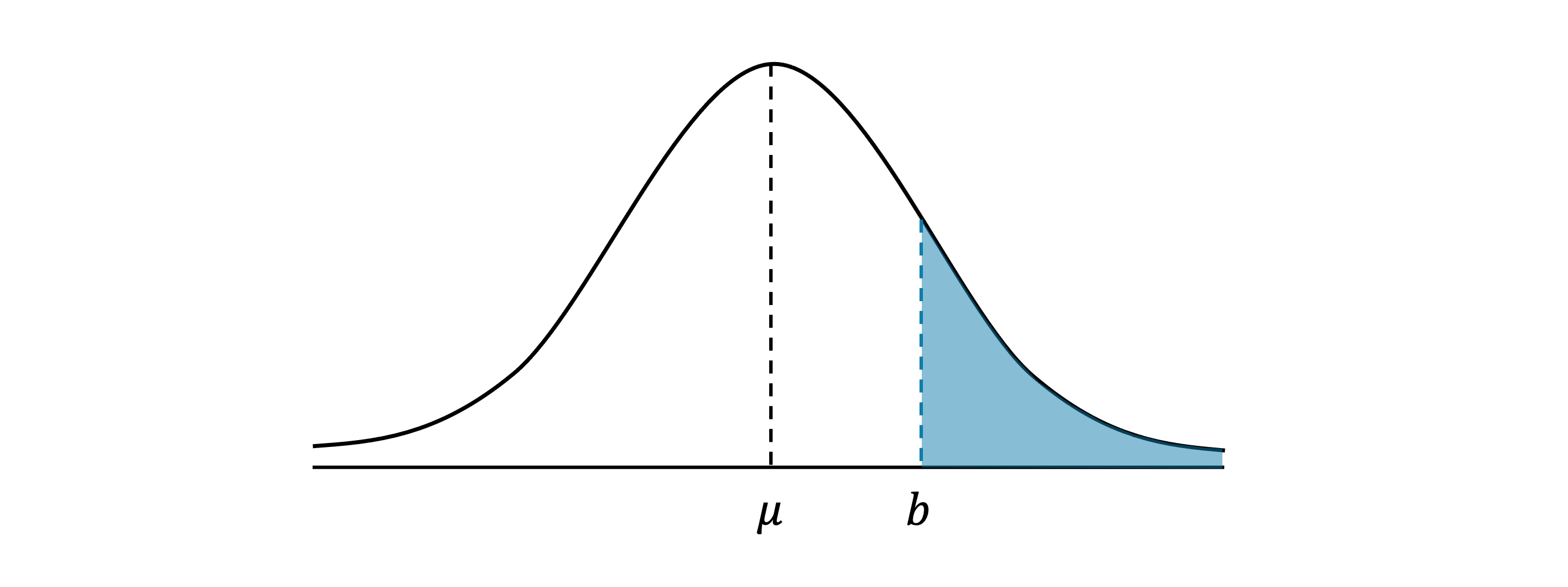
A normal distribution curve with mean μ and shaded area to the right of a vertical dashed line at b. The mean is labeled μ and point b is labeled b. — **Normal distribution with proportion of distribution above b shaded**

$P (X > b) = P (Z > z)$
- where $z$ is the $z$ -score of the value $b$
The total area under the curve is 1
- So $P (X > b) = 1 - P (X < b)$
If you are given the proportion (or probability) and want to work out the value of $b$ :
- subtract the proportion from 1
- find the cell in the standard normal table that is
  - equal to this result
  - or the lowest value that is greater than the proportion
- identify the $z$ -score by listing the relevant row and column
- convert the $z$ -score back into an actual value

Given the value of P(X > b) how do I find the value of b using a calculator?

You will need to use the Inverse Normal Distribution function again
Given $P (X > b) = p$
- Use $P (X < b) = 1 - P (X > b)$ to rewrite this as $P (X < b) = 1 - p$
- Then use the method for $P (X < b)$ to find $b$
Your calculator may have the tail option (left, right or centre)
- If so, you can use the Inverse Normal Distribution function straightaway by:
  - selecting right for the tail
  - and entering the area as $p$

Examiner Tips and Tricks

Always check your answer makes sense!

If $P (X > b)$ is less than 0.5 then $a$ should be bigger than the mean,
If $P (X > b)$ is more than 0.5 then $a$ should be smaller than the mean.

A sketch will help you see this.

Worked Example

The distribution of heights of all adult male bison in a particular herd of bison is approximately normal with a mean of 5.9 feet and standard deviation 0.16 feet. The rancher wants to select the tallest twenty percent of the bison to use for a breeding program.

What is the minimum height that an adult male bison must be to qualify for the breeding program?

Answer:

Method 1: Using the standard normal table

Draw a sketch of the situation

Because $P (X > b) = 0.2$ , is less than 0.5, $b$ should be bigger than the mean, i.e. $b$ lies to the right of the mean

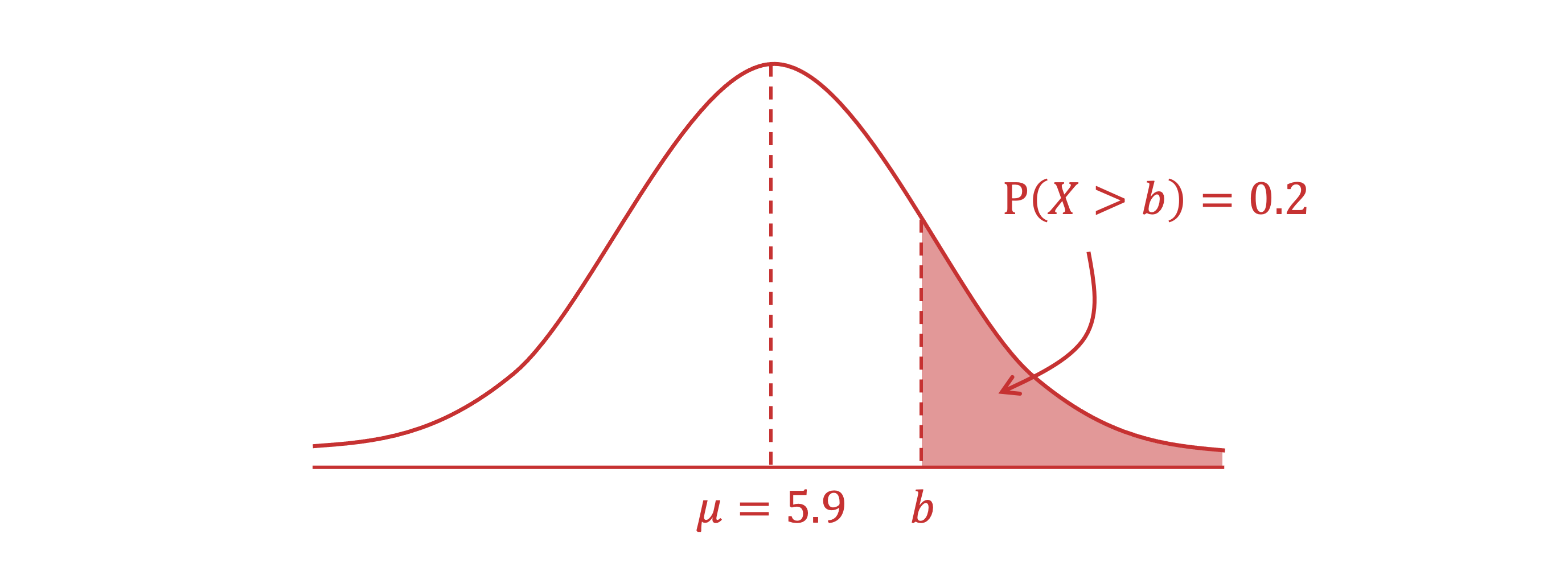
A normal distribution with the mean, μ, at 6.8. The area under the curve to the right of 'b' is highlighted and has probability, P(X > b) = 0.2.

Using the standard normal table, look at section with the positive $z$ -values as $b$ is above the mean

The standard normal table contains the proportions or percentages that are below a given value, i.e. to the left of the given value

You are given the proportion that lies to the right of $b$ , so use $P (X < b) = 1 - P (X > b)$ to find the proportion to the left of $b$

$1 - 0.2 = 0.8$

Find the cell that contains the value that is 0.8, if there is no exact value, find the smallest value that is greater than 0.8

0.8023 is the lowest value in the standard normal table that is greater than 0.8

Write down the $z$ -score from the corresponding row and column

$z = 0.85$

Convert the $z$ -score into an actual value, using $z = \frac{x - μ}{σ}$

$\begin{array}{rcl} 0.85 & = & \frac{b - 5.9}{0.16} \\ 0.85 \cdot 0.16 & = & b - 5.9 \\ 0.85 \cdot 0.16 + 5.9 & = & b \\ b & = & 6.036 \end{array}$

Explain the value in the context of the question

The minimum height that an adult male bison must be to qualify for the breeding program is 6.04 feet

Method 2: Using a calculator

Draw a sketch of the situation

Because $P (X > b) = 0.2$ , it is less than 0.5 , therefore $b$ should be bigger than the mean, i.e. to the right of the mean

You are given the proportion that lies to the right of $b$ , so use $P (X < b) = 1 - P (X > b)$ to find the proportion to the left of $b$

$1 - 0.2 = 0.8$

Write down the parameters for the situation

$P (X < b) = 0.8$

$μ = 5.9$

$σ = 0.16$

Enter these values into the Inverse Normal Distribution function on your calculator and calculate $b$

$b = 6.036$

Explain the value in the context of the question

The minimum height that an adult male bison must be to qualify for the breeding program is 6.04 feet

Last updated: 20 August 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Finding Proportions from Normal DistributionsNext:Estimating Parameters of Normal Distributions

Inverse Normal Calculations (College Board AP® Statistics)

Study Guide

Inverse normal calculations

Given the value P(X < a) how do I find the value of a using the standard normal table?

Given the value of P(X < a) how do I find the value of a using a calculator?

Examiner Tips and Tricks

Given the value of P(X > b) how do I find the value of a using the standard normal table?

Given the value of P(X > b) how do I find the value of b using a calculator?

Examiner Tips and Tricks

Worked Example

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Naomi C

Author: Dan Finlay