Finding Proportions from Normal Distributions (College Board AP® Statistics)

Study Guide

Test yourself

Written by: Naomi C

Reviewed by: Dan Finlay

Finding proportions from normal distributions

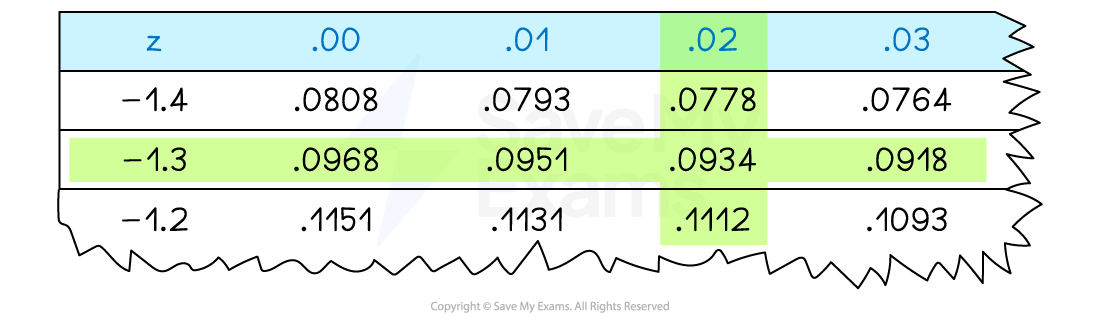
What is the standard normal table?

The proportion of a distribution of a variable $X$ within a particular interval can be determined using the standard normal table given to you in the exam
The standard normal table shows the proportion of the distribution (or percentage of values) that lie below a particular $z$ -score on a standard normal distribution
- A $z$ -score is the number of standard deviations that a value is from the mean
A $z$ -score on the table is made up from
- the row that corresponds to the correct units and tenths of the $z$ -score
- and the column that corresponds to the correct hundredths of the $z$ -score
  - e.g. a $z$ -score of -1.32 would use the row -1.3 and the column 0.02

Z-table section showing cumulative probabilities for z-values -1.4 to -1.2, and for decimals .00 to .03. Highlighted cell at z = -1.32, with value .0934. — **A section of the standard normal table**

You can also calculate proportions using your calculator

Examiner Tips and Tricks

When using technology to find the proportion of a distribution within a given interval it is essential to always show full working in Free Response Questions (FRQs). Write down any $z$ -scores and parameters that you use.

How do I find a proportion below a given value using a standard normal table?

The proportion of a distribution of a variable $X$ that lies below a given value is the area under the curve to the left of the given value
- $P (X < a) = p$

A normal distribution curve with mean μ and shaded area to the left of a vertical dashed line at a. The mean is labeled μ and point a is labeled a. — **Normal distribution with proportion of distribution less than the value 'a' shaded**

To find this proportion using the standard normal table:
- find the $z$ -score for the value $a$
- use this $z$ -score to locate the appropriate row and column in the standard normal table
- identify the cell that corresponds to this row and column
  - the value in this cell is $P (Z < z)$ , the proportion of the distribution that lies below the $z$ -score
  - this is equal to $P (X < a)$ , the proportion of the distribution that lies below $a$

How do I find a proportion below a given value using a calculator?

You need a calculator that can calculate cumulative normal probabilities
You want to use the Normal Cumulative Distribution function
- This is sometimes shortened to NCD, Normal CD or Normal Cdf
When using a calculator to find a proportion you can use the given values
- You do not need to enter the associated $z$ -scores first
  - However you should write down the $z$ -score in the exam to support your work
To find $P (X < a) = p$ , you will need to enter:
- The lower bound
  - this needs to be a value that is sufficiently smaller than the mean
  - an easy option is to input lots of 9's for the lower bound with a negative sign (-99999999... or -10⁹⁹)
- The upper bound
  - this will be the value $a$
- The mean, $μ$
- The standard deviation, $σ$

How do I find a proportion above a given value using a standard normal table?

The proportion of a a distribution of a variable $X$ that lies above a given value is the area under the curve to the right of the given value
- $P (X > b) = p$

A normal distribution curve with mean μ and shaded area to the right of a vertical dashed line at b. The mean is labeled μ and point b is labeled b. — **Normal distribution with proportion of distribution above b shaded**

The total area under the curve is 1
- So $P (X > b) = 1 - P (X < b)$
To find this proportion using the standard normal table:
- find the $z$ -score for the value $b$
- use this $z$ -score to locate the appropriate row and column in the standard normal table
- identify the cell that corresponds to this row and column
- subtract the value in this cell from 1
  - the result is $P (Z > z)$ , the proportion of the distribution that lies above the $z$ -score
  - this is equal to $P (X > b)$ , the proportion of the distribution that lies above $b$

How do I find a proportion above a given value using a calculator?

You will still use the Normal Cumulative Distribution function
To find $P (X > b) = p$ , you will need to enter:
- The lower bound
  - this will be the value $b$
- The upper bound
  - this needs to be a value that is sufficiently bigger than the mean
  - an easy option is to input lots of 9's for the lower bound with a positive sign (99999999... or 10⁹⁹)
- The mean, $μ$
- The standard deviation, $σ$

How do I find a proportion in a given range using a standard normal table?

The proportion of a distribution that lies in a given interval is the area under the curve between the lower bound value, $a$ , and the upper bound value, $b$
- $P (a < X < b) = p$

A normal distribution curve with mean μ and shaded area to the right of a vertical dashed line at a and the left of a vertical dashed line at b. — **Normal distribution with proportion of distribution between a and b shaded**

To find this proportion using the standard normal table:
- find the $z$ -score for both the value $a$ and the value $b$
- use these $z$ -scores in the standard normal table to find the proportion of the distribution that lies below each value
- subtract the proportions of the two $z$ -scores
  - $P (Z < z_{b}) - P (Z < z_{a})$
  - This is equal to $P (X < b) - P (X < a)$ ,the proportion of the distribution that lies between $a$ and $b$

How do I find a proportion in a given range using a calculator?

You will still use the Normal Cumulative Distribution function
To find $P (a < X < b) = p$ , you will need to enter:
- The lower bound
  - this will be the value $a$
- The upper bound
  - this will be the value $b$
- The mean, $μ$
- The standard deviation, $σ$

Examiner Tips and Tricks

It is often useful to sketch a quick diagram of the section of the distribution that you are looking for.

Worked Example

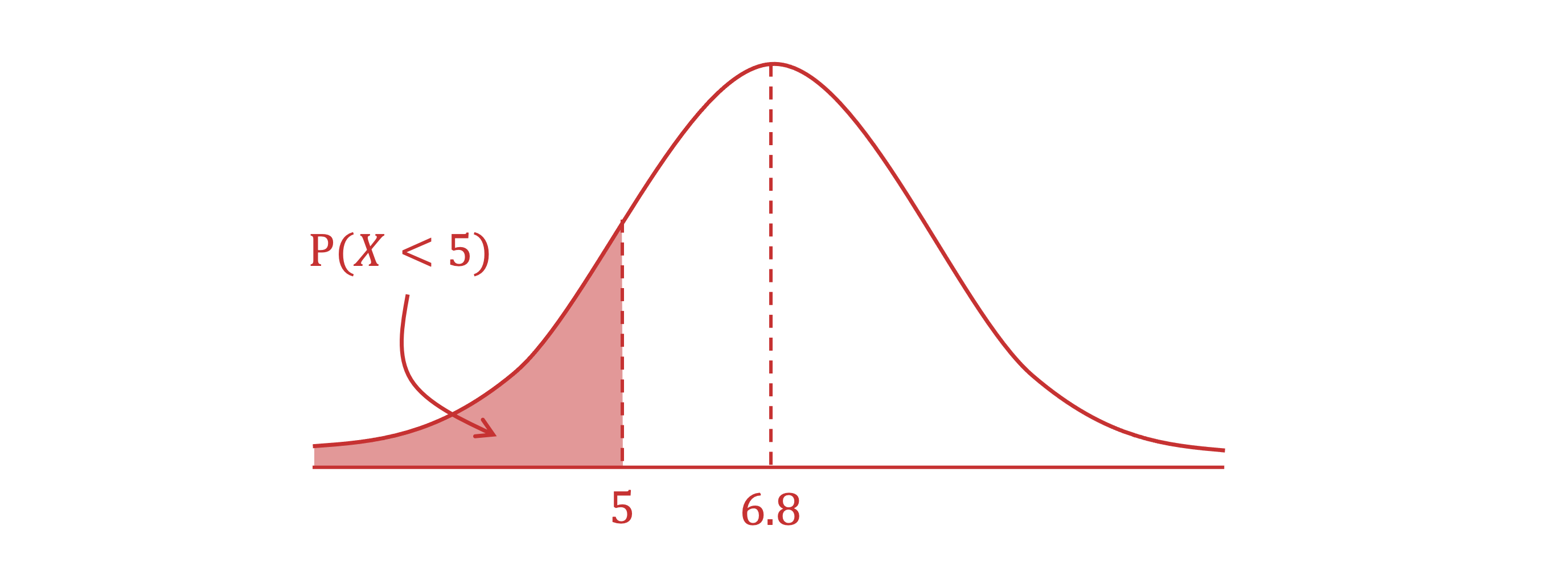
An environmental group conducted a study measuring the dissolved oxygen content in a large number of samples of water to determine the water quality of a local lake. The results of the study found a mean level of 6.8 mg/l and a standard deviation of 0.7mg/l. A water sample with a dissolved oxygen content of less than 5 mg/l is considered to be unhealthy for fish.

What proportion of the water samples are considered to contain levels of dissolved oxygen that are unhealthy for fish?

Answer:

Method 1: Using the standard normal table

Define your variable and its distribution

Let $X$ be the level of dissolved oxygen in the water samples

The distribution of $X$ is normal with mean 6.8 and standard deviation 0.7

Draw a sketch describing the proportion of the distribution you are trying to find and write a probability statement for $X$

Normal distribution with mean 6.8 and an area shaded to the left of x=5. Dashed vertical lines at x=5 and x=6.8.

Calculate the $z$ -score for the value of 5mg/l, using $z = \frac{x - μ}{σ}$

$\begin{array}{rcl} z & = & \frac{5 - 6.8}{0.7} \\ = & - 2.5714 . . . \end{array}$

A value of 5mg/l lies 2.57 standard deviations below the mean

Using the $z$ -score 2.57, find the row labeled -2.5 and the column labeled 0.7 on the standard normal table, and the cell where they intersect

Write a probability statement for $Z$

$P (Z < - 2.57) = 0.0051$

Explain the value in the context of the question, leaving the value from the table to 4 significant figures

The proportion 0.0051 (or 0.51%) of water samples taken contain an unhealthy dissolved oxygen level of less than 5mg/l

Method 2: Using a calculator

Define your variable and its distribution

Let $X$ be the level of dissolved oxygen in the water samples

The distribution of $X$ is normal with mean 6.8 and standard deviation 0.7

Draw a sketch describing the proportion of the distribution you are trying to find and write a probability statement for $X$

Even though you do not need to enter it into your calculator, it is a good idea to write down the calculation of the $z$ -score for the value of 5mg/l, using $z = \frac{x - μ}{σ}$ ,

$\begin{array}{rcl} z & = & \frac{5 - 6.8}{0.7} \\ = & - 2.5714 . . . \end{array}$

Write a probability statement for $Z$

$P (Z < - 2.57)$

Write down the parameters for the situation

lower bound = -10⁹⁹

upper bound = 5

$μ = 6.8$

$σ = 0.7$

Enter these values into the Normal Cumulative Distribution function on your calculator

$P (X < 5) = 0.0051$

Explain the value in the context of the question

The proportion 0.0051 (or 0.51%) of water samples taken contain an unhealthy dissolved oxygen level of less than 5mg/l

Last updated: 24 September 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Comparing Normal DistributionsNext:Inverse Normal Calculations

Finding Proportions from Normal Distributions (College Board AP® Statistics)

Study Guide

Finding proportions from normal distributions

What is the standard normal table?

Examiner Tips and Tricks

How do I find a proportion below a given value using a standard normal table?

How do I find a proportion below a given value using a calculator?

How do I find a proportion above a given value using a standard normal table?

How do I find a proportion above a given value using a calculator?

How do I find a proportion in a given range using a standard normal table?

How do I find a proportion in a given range using a calculator?

Examiner Tips and Tricks

Worked Example

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Naomi C

Author: Dan Finlay