AP®StatisticsCollege BoardStudy GuidesUnit 1: Exploring One-Variable DataThe Normal DistributionComparing Normal Distributions

Comparing Normal Distributions (College Board AP® Statistics)

Study Guide

Test yourself
Naomi C

Written by: Naomi C

Reviewed by: Dan Finlay

Comparing normal distributions

  • Two normal distributions can be compared by examining their parameters

    • the mean, mu

    • and the standard deviation, sigma

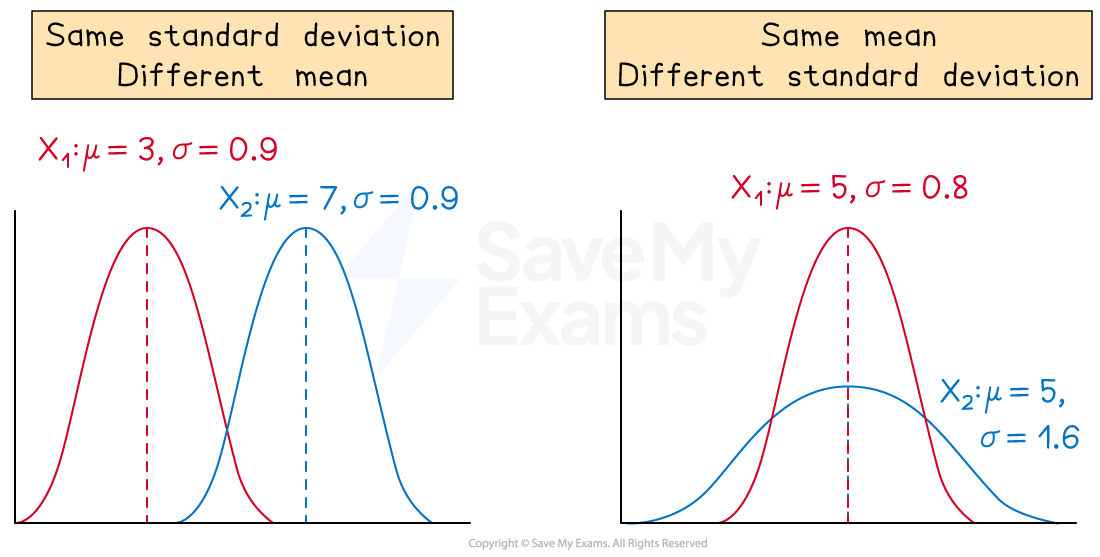
  • Two normal distributions with the same mean but different standard deviations will lie in the same position but have different shapes

    • The distribution with the smaller standard deviation will be taller and steeper

    • The distribution with the greater standard deviation will be shorter and wider

  • Two normal distributions with the same standard deviation but different means will have the same shape but lie in different positions

    • The distribution with the smaller mean will be positioned to the left

    • The distribution with the greater mean will be positioned to the right

Two graphs show normal distribution comparisons. Left: same standard deviation (0.9), different means (3, 7). Right: same mean (5), different standard deviations (0.8, 1.6).
Comparative normal distributions

Worked Example

Factory A manufactures batteries with a mean battery life of 4.1 hours and standard deviation of 0.3 hours. Factory B manufactures a different brand of batteries with a mean battery life of 3.7 hours and standard deviation of 0.2 hours. Compare the different brands of batteries that are manufactured in the two factories.

Answer:

Compare the mean battery life for the batteries manufactured in each factory

table row cell 4.1 end cell greater than cell 3.7 end cell row cell mu subscript A end cell greater than cell mu subscript B end cell end table

Compare the standard deviation of the battery life for the batteries manufactured in each factory

table row cell 0.3 end cell greater than cell 0.2 end cell row cell sigma subscript A end cell greater than cell sigma subscript B end cell end table

Compare the two parameters using the context of the question

The mean battery life of the batteries manufactured in factory A (4.1 hours) is greater than the mean battery life of those manufactured in factory B (3.7 hours)

This means that on average the batteries from factory A will last longer

The standard deviation of the battery life of the batteries manufactured in factory A (0.3 hours) is also greater than the standard deviation of the battery life of those manufactured in factory B (0.2 hours)

This means that there is a greater variation in the battery life of those batteries manufacture in factory A than those from factory B

Comparing z-scores

  • Two values can be compared by examining their z-scores

    • The z-score indicates the number of standard deviations that a data point lies from the mean of its distribution

  • When comparing two values within the same data set

    • the data point with the greater absolute value z-score lies further from the mean

  • When comparing two values in different data sets

    • the data point with the greater absolute value z-score has a greater relative position from its mean than the other data point has from its mean

Worked Example

A math major at college decided to complete a study on the recovery time after completing different types of exercise. She measured the time taken in minutes for the heart rate of an individual student to return to its resting rate after completing 10 mins of swimming. She then repeated this measurement on the same student after they completed 10 minutes of running on another day. This study was completed for a large sample of students.

The summary statistics for the study are as follows:

Activity

Mean

Standard Deviation

Swimming

3.7

0.8

Running

4.2

1.1

Kenzie had a recovery time of 3.2 minutes after swimming and 3.6 minutes after running.

For which activity did she recover relatively quicker from?

Answer:

Kenzie recovered from both activities in less than the mean time but as the distributions are different the z-scores must be compared

Find the z-score for each activity using z equals fraction numerator x minus mu over denominator sigma end fraction

table row cell z subscript s w i m m i n g end subscript end cell equals cell fraction numerator 3.2 minus 3.7 over denominator 0.7 end fraction end cell row blank equals cell negative 0.7142... end cell row blank almost equal to cell negative 0.714 end cell end table

table row cell z subscript r u n n i n g end subscript end cell equals cell fraction numerator 3.6 minus 4.2 over denominator 1.1 end fraction end cell row blank equals cell negative 0.5454... end cell row blank almost equal to cell negative 0.545 end cell end table

Compare absolute values of the two z-scores

table row cell vertical line z subscript s w i m m i n g end subscript vertical line end cell greater than cell vertical line z subscript r u n n i n g end subscript vertical line end cell row cell 0.714 end cell greater than cell 0.545 end cell end table

The absolute value of the z-score for swimming is greater than the value for running, so the recovery time after swimming is a greater number of standard deviations from the mean

As both actual z-scores are negative, they are both below the mean, so the lower value for swimming means that the recovery time is further below the mean than the value for running

Kenzie recovers relatively quicker from swimming than from running

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Standardized z-scoresNext:Finding Proportions from Normal Distributions
    Author
    Reviewer
    Naomi C

    Author: Naomi C

    Expertise: Maths

    Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.