Study GuidesExam QuestionsPast Papers
AP®StatisticsCollege BoardStudy GuidesUnit 1: Exploring One-Variable DataSummary StatisticsSkewness of Data

Skewness of Data (College Board AP® Statistics): Study Guide

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on

Skewness of data

What is skewness?

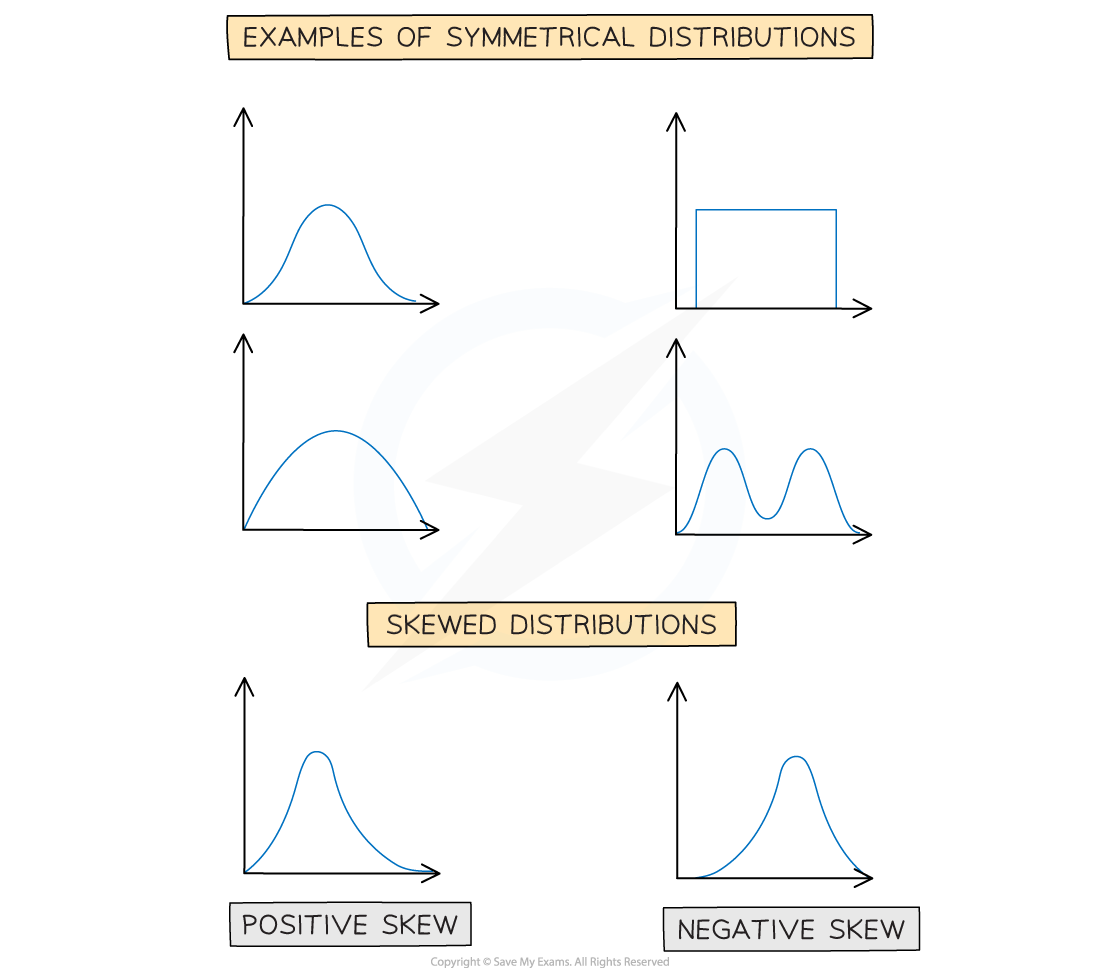
  • When a set of data is plotted on a graph, the shape of the distribution of the data can be seen

  • The shape of the distribution can be

    • symmetrical

    • or non-symmetrical

      • There are many different shapes that non-symmetrical distributions can take

  • Skewness describes the direction in which a non-symmetrical distribution of data is leaning

    • A distribution that has its tail on the right side has positive skew

    • A distribution that has its tail on the left side has negative skew

A chart with examples of symmetrical distributions and skewed distributions. The symmetrical distributions include: bell curve, uniform, bimodal; and the skewed distributions include: positive skew (tail right), negative skew (tail left).

Examiner Tips and Tricks

It is a common mistake for students to look at the peaks of the distributions and get the skewness the wrong way round!

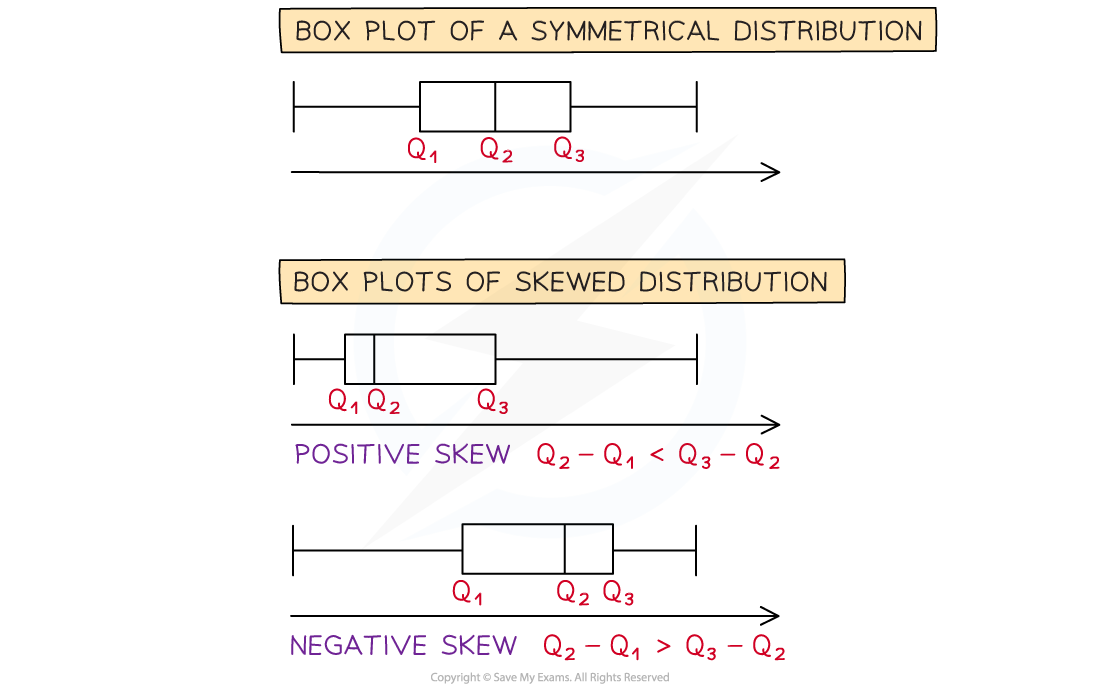
How do I find the skewness from a boxplot?

  • If a set of data is shown on a boxplot then looking at the differences between the quartiles can help to decide how it is skewed

    • If the median is roughly in the middle of the first and third quartiles, then the distribution is approximately symmetric

      • Q3 -  Q2 almost equal to Q2- Q1

    • If the median is closer to the first quartile, then the distribution has positive skew

      • Q3 -  Q2 > Q2- Q1

    • If the median is closer to the third quartile then the distribution has negative skew

      • Q3 -  Q2 < Q2- Q1

Diagram showing three box plots. The first boxplot shows a symmetrical distribution with equal quartile distances, the second shows a positively skewed distribution with a smaller difference between the first and second quartiles than the second and third quartiles and a longer right whisker, and the third shows a negatively skewed distribution with a larger difference between the first and second quartiles than the second and third quartiles and a longer left whisker.

How do I find the skewness from the median and the mean?

  • It is possible to find the skewness if given the median and the mean of a data set

    • In a symmetric distribution

      • the median and the mean are roughly the same

      • median almost equal to mean

    • In a positively skewed distribution 

      • median < mean

    • In a negatively skewed distribution 

      • mean < median

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Five-Number Summary & BoxplotsNext:Comparing Data using Summary Statistics
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.