Cumulative Graphs (College Board AP® Statistics)

Cumulative graphs

What is cumulative frequency?

• Cumulative frequency is the sum of all the different frequencies up to and including a given point

• In a frequency table, the cumulative frequency of a row is

  • the frequency of that row, plus the frequency in the row before, plus the frequency in the row before that... etc.

How do I draw a cumulative graph?

• A cumulative graph shows the cumulative frequency on the -axis instead of the frequency

• This is easiest shown with an example

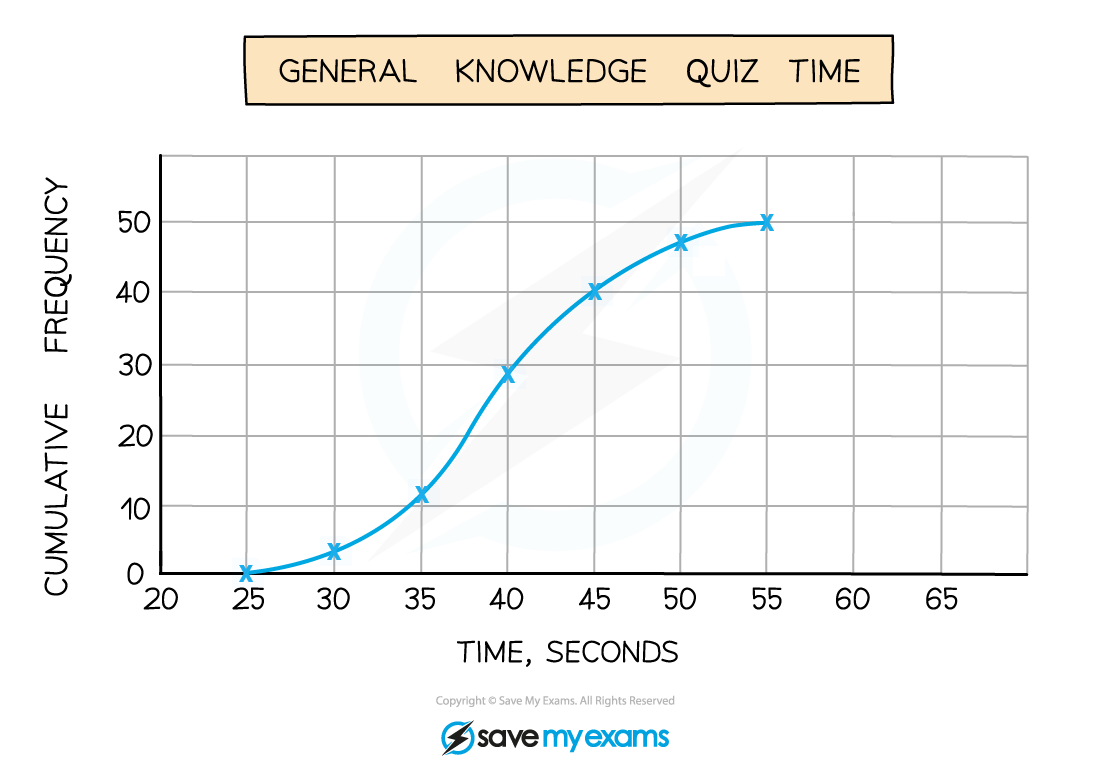
  • The times taken to complete a short general knowledge quiz taken by 50 students are shown in the table below:

    Time taken ( seconds)	Frequency
    	3
    	8
    	17
    	12
    	7
    	3
    Total	50

  • The cumulative frequency is the running total of the frequencies

    Time taken ( seconds)	Frequency	Cumulative Frequency
    	3	3
    	8	3 + 8 = 11
    	17	11 + 17 = 28
    	12	28 + 12 = 40
    	7	40 + 7 = 47
    	3	47 + 3 = 50
    Total	50

• We can now draw the cumulative graph

  • The most important part is that cumulative frequency is plotted against the end (upper bound) of the interval

  • Consider the second row ()

    • You do not know the exact times of the 8 students in this group

    • They could have taken any time between 30 and 35 seconds

    • You know for sure that all 8 students are included by 35 seconds

  • Points are usually joined up to make a smooth curve

  • In general, cumulative graphs have a stretched S-shape

    • A cumulative graph will never come back towards the -axis

• Here is the final cumulative graph for the quiz times

How do I estimate medians and quartiles from cumulative graphs?

• The median is the value on the -axis that comes from half of the total cumulative frequency on the -axis

• The first (lower) quartile is the value on the -axis that comes from a quarter of the total cumulative frequency on the -axis

• The third (upper) quartile is the value on the -axis that comes from three quarters of the total cumulative frequency on the -axis

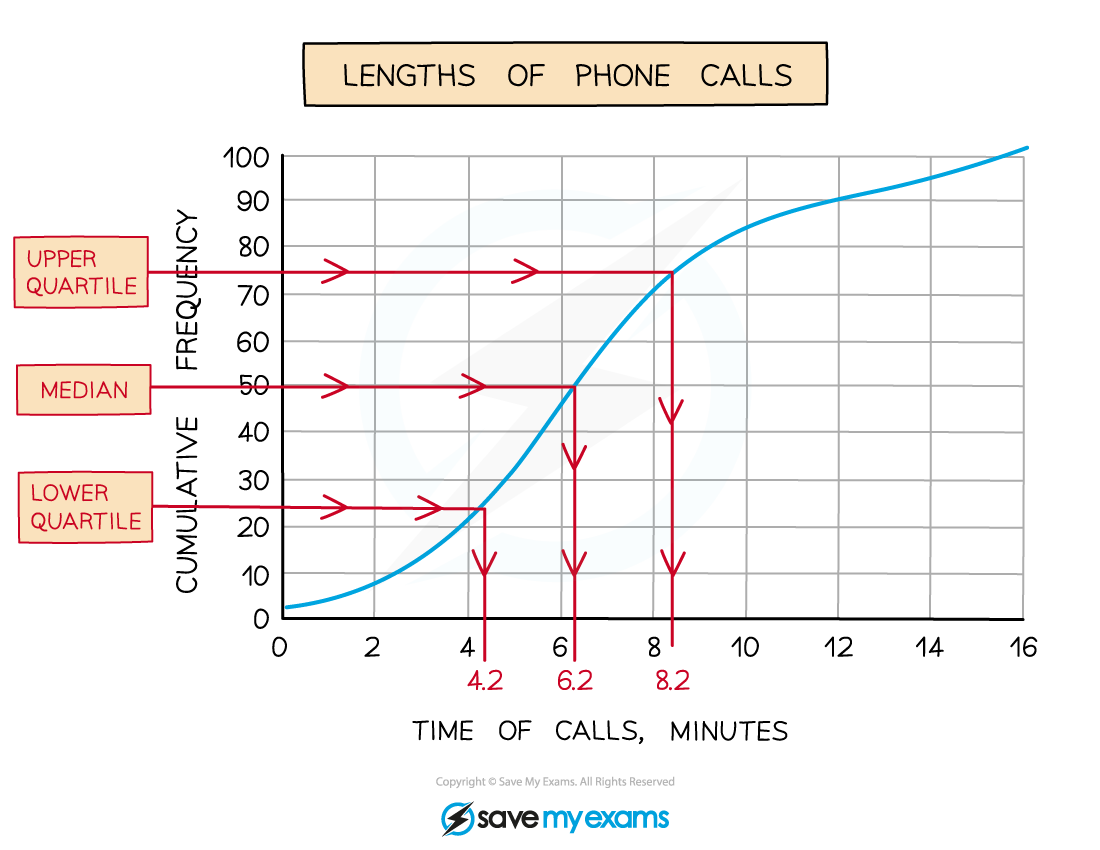
• In the cumulative graph for the lengths of phone calls shown below

  • the total cumulative frequency on the -axis is 100, so from the rules above

    • the median is 6.2 minutes

    • the lower quartile is 4.2 minutes

    • the upper quartile is 8.2 minutes