Comparing Univariate Graphs (College Board AP® Statistics)

Exam Tip

In the exam, always remember to:

• use numbers from each graph in your comparisons,

• explain clearly which part of the graph you are talking about,

• relate any numbers or calculations back to the context of the question.

Exam Tip

If the graphs do not have any unusual features, you should still write "no unusual features" to show the examiner that you have checked for these.

Worked Example

The number of books bought during the opening week of a new bookshop is shown below. The shopkeeper wants to investigate shopping patterns between male and female customers.

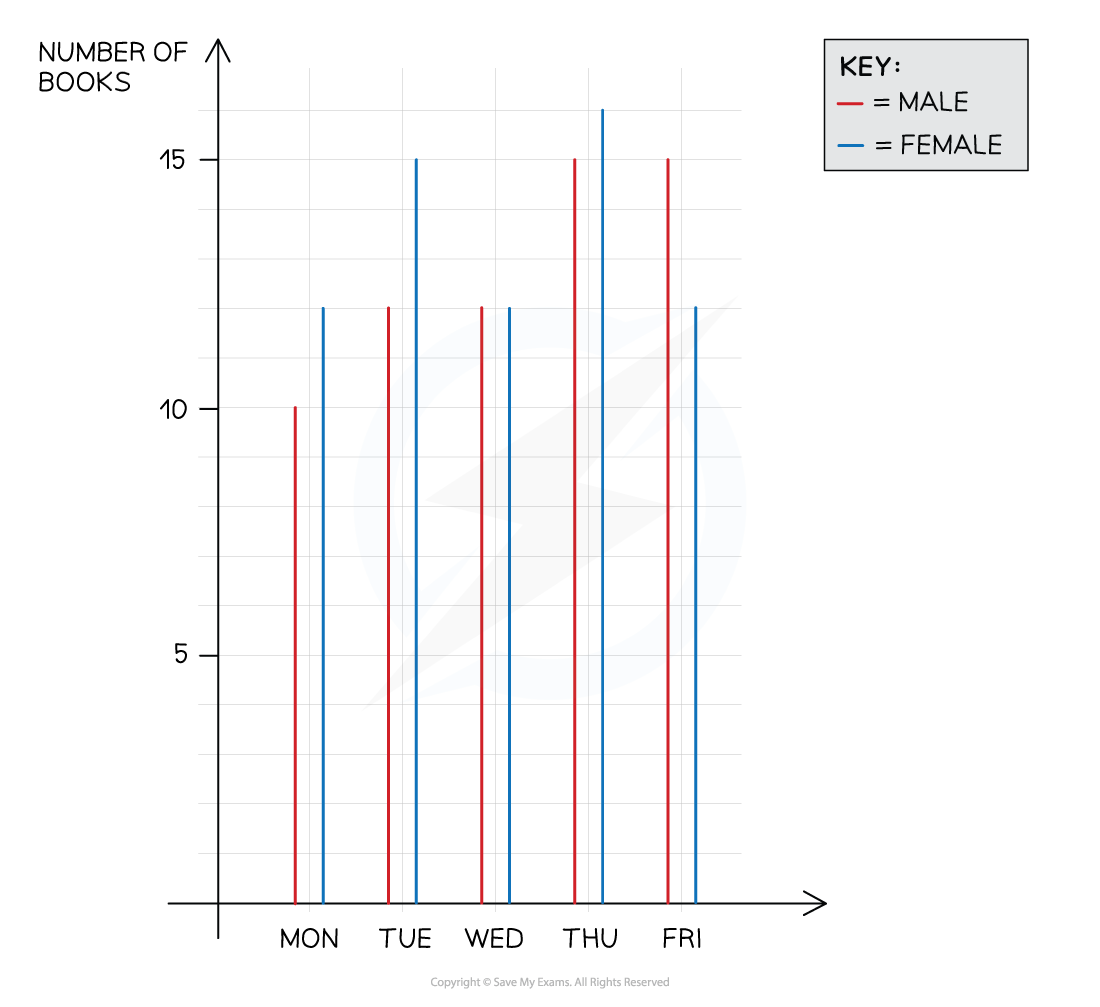
(a) Compare the number of books bought by male and female customers during the opening week.

Answer:

You need to compare:

• the centers of the data (either a mean, median or mode)

• the spread of the data (either a range, interquartile range or standard deviation)

• the shape of the distributions (skew, symmetry)

• and any unusual features (outliers, gaps, clusters, multiple peaks)

Comparing the centers of the data, the number of books bought by male customers has two consecutive modes on Thursday and Friday whereas the number of books bought by female customers has one mode on Thursday
This suggests that Thursday, in particular, was a popular day

Comparing the spread of the data, the number of books bought by male customers has a range of 15 - 10 = 5 whereas the number of books bought by female customers has a range of 16 - 12 = 4, which is lower than that of male customers
This suggests that male customers have a greater variability in the number of books bought

Comparing the shapes of the distributions, the number of books bought by male customers has a strong negative (left) skew whereas the number of books bought by female customers has a weak negative (left) skew
This suggests that the number of books bought by males and females generally increased over the week

Comparing any unusual features, neither graph has any outliers or gaps
The number of books bought by male customers is always either increasing or staying the same, rising to a peak that spans both Thursday and Friday
The number of books bought by female customers has two peaks (bimodal) which form slight clusters around Tuesday and around Thursday

(b) Give one reason as to why the shopkeeper should not use the data shown to predict future shopping patterns.

Answer:

Reread the sentences at the beginning of the question

This data is for the opening week of the bookshop only

State that this is unrepresentative of a normal week

Give a specific real life example

The data shown is for the opening week of the bookshop, so it is unlikely to be representative of a normal week

Over time, the number of books bought may increase as the bookshop becomes more popular, or decrease if the customers lose interest