Work-Energy Theorem (College Board AP® Physics 1: Algebra-Based): Exam Questions

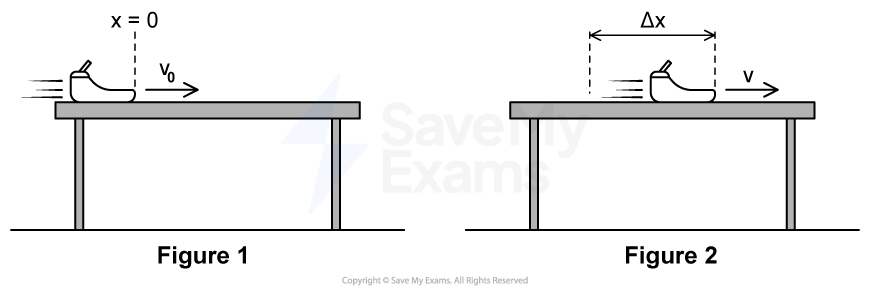
A small sled slides across a rough horizontal table with an initial velocity . The coefficient of kinetic friction between the sled and the table is . The total mass of the sled is . The sled has velocity after traveling a horizontal distance , as shown in Figure 2.

i) On the dot in Figure 3, which represents the sled, draw and label the forces (not components) that act on the sled when the sled is at the position shown in Figure 2. Each force must be represented by a distinct arrow starting on and pointing away from the dot.

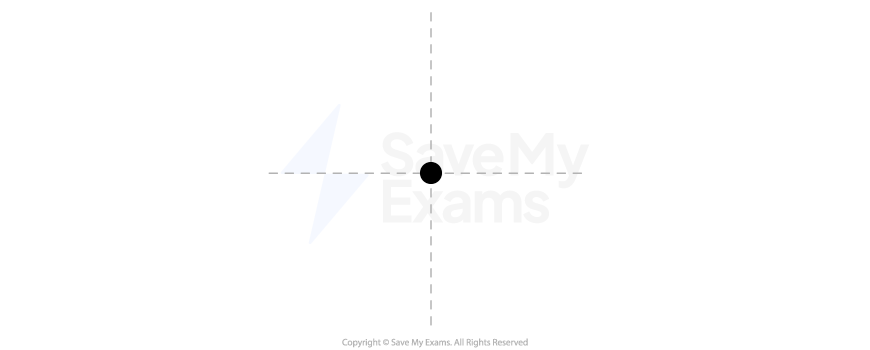
Figure 3

Express your answers to the following in terms of , , , , and physical constants, as appropriate.

ii) Derive an expression for the work done on the sled when the sled has traveled a horizontal distance . Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

iii) Starting with the work-energy principle, derive an expression for the velocity of the sled when the sled has traveled a horizontal distance . Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

Figure 1

A block of mass is pulled up a ramp by a string connected to a motor that is attached to the floor. The angle between the ramp and the horizontal is , as shown in Figure 1. The string passes over a pulley with negligible friction. Friction between the block and the ramp is negligible. The string and pulley both have negligible mass. The pulley is at height above the table. The motor exerts a constant force of tension on the string, and the block remains in contact with the ramp at all times as it travels a horizontal distance .

i) On the dot in Figure 2, which represents the block, draw and label the forces (not components) that act on the block when it is being pulled up the ramp. Each force must be represented by a distinct arrow starting on and pointing away from the dot.

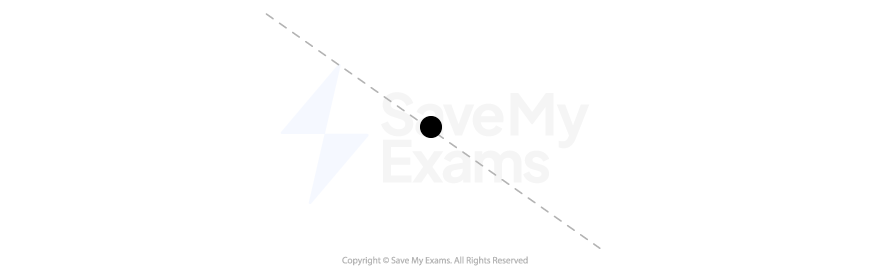
Figure 2

Express your answers to the following in terms of , , , and physical constants as appropriate.

ii) Derive an expression for the work done by the string on the block when the block has traveled a horizontal distance . Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

iii) Starting with the work-energy principle, derive an expression for the change in the block's kinetic energy when the block has traveled a horizontal distance . Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

Figure 1

Block 1 of mass is initially at position on a horizontal surface and is in contact with an uncompressed spring with spring constant . Block 1 is pushed to the left along the surface from position to , compressing the spring by an amount , as shown in Figure 1. There is negligible friction between the surface and the block to the left of . There is non-negligible friction between the surface and the block to the right of . The coefficient of kinetic friction between the block and the rough track is .

Block 1 is released from rest from position . When it is at , Block 1 loses contact with the spring and enters the rough part of the track, eventually coming to rest at position .

Block 1 is replaced by Block 2, which has a mass such that . Block 2 is pushed against the spring until it is compressed by an amount and is then released.

Indicate whether the position of Block 2 when it comes to rest is greater than, less than, or equal to .

⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ ‎ ‎ ‎‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽

Justify your reasoning using qualitative reasoning beyond referencing equations.

Starting with the work-energy principle, derive an expression for the final position of Block 2. Express your answer in terms of , , , , and physical constants, as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

Justify whether or not the expression you derived for in part b) is consistent with the claim made in part a).

Figure 1

In Experiment 1, a block is initially at position and in contact with an uncompressed spring of negligible mass. The block is pushed back along a frictionless surface from position to , as shown in Figure 1. The block compresses the spring by an amount . The block is then released. At the block enters a rough part of the track and eventually comes to rest at final position . The coefficient of kinetic friction between the block and the rough track is .

In Experiment 2, the spring is compressed twice as much, to .

Indicate whether the final position of the block in Experiment 2 will be greater than, equal to, or less than .

⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ ‎ ‎ ‎‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽

Justify your reasoning.