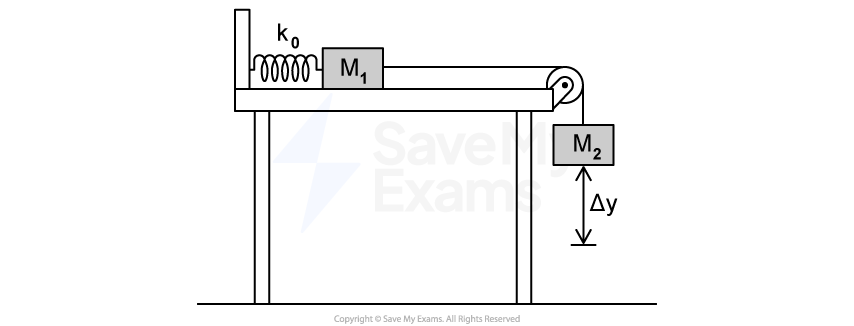
A car drives along an uphill road. The system is defined as the car only.
Identify the type or types of energy the system has. Justify your reasoning.
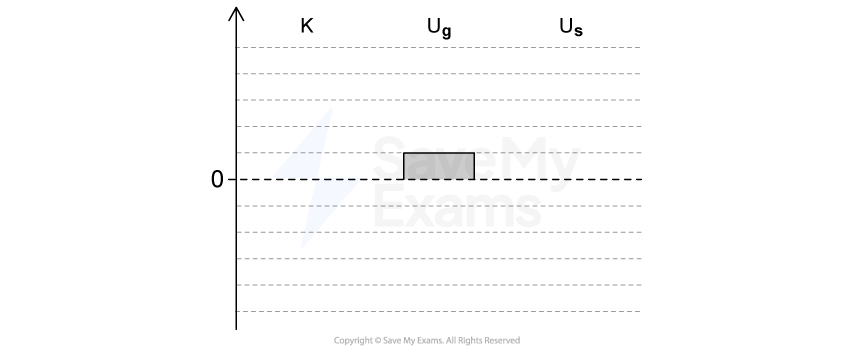
A mass oscillates vertically on a spring. Describe the composition of the system for it to have kinetic and spring potential energy only.
The same mass oscillates vertically on the same spring. Describe the composition of the system for it to have gravitational potential and kinetic energy only.
The same mass oscillates vertically on the same spring. Describe the composition of the system for it to have gravitational and spring potential energy and kinetic energy.
Did this page help you?