Simple Harmonic Motion (College Board AP® Physics 1: Algebra-Based): Exam Questions

A small mass is attached to an ideal horizontal spring of spring constant and is set into simple harmonic motion. The system oscillates on a frictionless surface. The mass is displaced by an initial amplitude and released from rest. The oscillations have a period .

Derive an expression for the maximum force exerted on the small mass by the spring. Express your answer in terms of , , and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

Figure 1

A cart on a horizontal surface is attached to a spring. The other end of the spring is attached to a wall. The cart is initially held at rest, as shown in Figure 1. When the cart is released, the system consisting of the cart and spring oscillates between the positions and .

Figure 2

When the cart is at position and momentarily at rest, a block is dropped onto the cart, as shown in Figure 2. The block sticks to the cart, and the block-cart-spring system continues to oscillate between and . The masses of the cart and the block are and , respectively and the spring has a spring constant .

i) The frequency of oscillation before the block is dropped onto the cart is . The frequency of oscillation after the block is dropped onto the cart is . Determine an expression for the ratio .

ii) Derive an expression for the acceleration of the block-cart-spring system at position . Express your answer in terms of , , and . Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

A small block of mass is attached to a horizontal ideal spring with a spring constant . The block oscillates on a frictionless surface with an amplitude . A student adds a second identical block onto the first block at maximum displacement. The new system continues oscillating. Air resistance is negligible.

Derive an expression for the new frequency of oscillation after the second block is added. Express your answer in terms of , , and fundamental constants.

The period of the system is when the additional mass is added. The additional mass is then removed, and the spring constant is halved. The period of this system is now .

Indicate whether is greater than, equal to, or less than after the changes to the system. Justify your prediction.

A small mass is attached to an ideal horizontal spring of spring constant and is set into simple harmonic motion. The system oscillates on a frictionless surface. The mass is displaced by an initial amplitude and released from rest. It reaches maximum speed and maximum acceleration . The motion follows the equation:

where is the frequency of oscillation.

A second identical system is made to oscillate in the same way at the same time, but this system experiences a constant friction force. After 10 s, this system has maximum acceleration . Indicate whether is greater than, less than or equal to .

Justify your answer.

An object of mass rests on a horizontal surface and is attached to the end of a light, ideal spring of spring constant . The other end of the spring is attached to a vertical rigid wall.

Derive an expression for the acceleration of the object in the direction when it is displaced a distance from equilibrium, in terms of , and and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

Figure 1

A spring of unknown spring constant is attached to a ceiling. A lightweight hanger is attached to the lower end of the spring, and a motion detector is placed on the floor facing upward directly under the hanger, as shown in the figure above. The bottom of the hanger is 1.00 m above the motion detector.

An object of mass is then placed on the hanger and allowed to come to rest at the equilibrium position, such that the bottom of the hanger is distance below its initial position. The spring is then stretched downward from equilibrium and released at time = 0 s. The motion detector records the height of the bottom of the hanger as a function of time. The output from the motion detector is shown in Figure 2.

Figure 2

i) On Figure 3 below, sketch a free body diagram of the object at equilibrium.

Figure 3

ii) Determine an expression for in terms of , and physical constants as appropriate.

iii) Starting with the equation for the period of a mass on a spring, derive an expression for the frequency of the object on the spring in terms of and physical constants as appropriate.

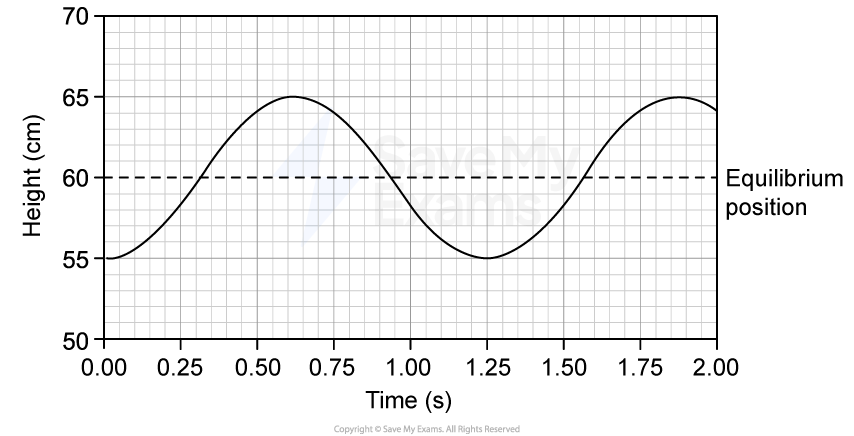
Figure 1

Two ideal springs, 1 and 2, of spring constant and respectively, are connected end to end. A block of mass is attached to the end of Spring 2 and the other end of Spring 1 is fixed to a wall. The block is displaced to the left of the spring's equilibrium position, , and held stationary at position , as shown in Figure 1. The block is then released at time .

At time , the block's displacement is and it is travelling to the right.

i) Derive an expression for the effective spring constant of Spring 1 and Spring 2 in terms of , and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

ii) Starting with the equation for the displacement of an object in simple harmonic motion, derive an expression for time in terms of , , and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

Figure 1

A pendulum is displaced to angle before being released. Upon being released, the pendulum has angular acceleration . The string has length and the bob at the end has mass .

i) On the diagram in Figure 1, draw and label arrows that represent the forces (not components) that are exerted on the pendulum bob. Each force in your diagram must be represented by a distinct arrow starting on, and pointing away from, the point at which the force is exerted on the bob.

ii) Determine an expression for the tangential acceleration of the pendulum the moment it is released in terms of and physical constants as appropriate.

iii) Derive an expression for the period of this pendulum. Express your answer in terms of , and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

Figure 1

A student conducts an investigation to determine the relationship between the period of oscillation of a system consisting of a block and attached springs. The student starts with a block of mass attached to a single ideal spring of spring constant , as shown in the first diagram in Figure 1. The student holds the block so that the spring is neither stretched nor compressed at a vertical height 1.00 m above a motion detector. The student releases the block from rest and records the period of oscillation for the system consisting of the single spring and block. An additional identical spring is attached in parallel, as shown in the second diagram in Figure 1, and the procedure is repeated for springs. This procedure is repeated through springs.

Derive an expression for as a function of . Express your answer in terms of , , , and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

Figure 1

A student conducts an investigation to determine the relationship between the period of oscillation of a system consisting of a block and attached springs. The student starts with a block of mass attached to a single ideal spring of spring constant , as shown in the first diagram in Figure 1. The student holds the block so that the spring is neither stretched nor compressed at a vertical height 1.00 m above a motion detector. The student releases the block from rest and records the period of oscillation for the system consisting of the single spring and block. An additional identical spring is attached in parallel, as shown in the second diagram in Figure 1, and the procedure is repeated for springs. This procedure is repeated through springs.

Figure 2

The student plots the data for as a function of as shown in Figure 2.

Draw the best-fit line for the data.

The students determine the relationship between and to be:

The mass of the block is measured to be . Using the graph, calculate an experimental value for the spring constant for a single spring.