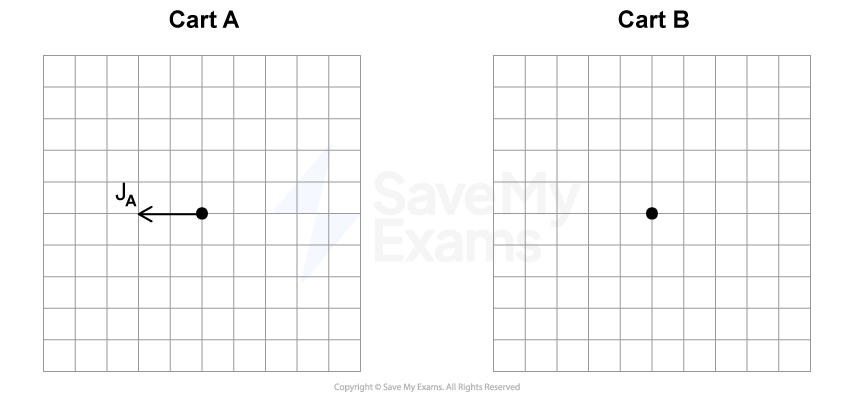
A ball is dropped from rest from a height of above the ground.
Using kinematic equations, derive an expression for the velocity of the ball in terms of just before it hits the ground and state any assumptions made.
When the ball is dropped, air resistance is present.
On the axis provided in Figure 1 sketch a velocity-time graph of the motion of the ball from the point of release to when it hits the ground.
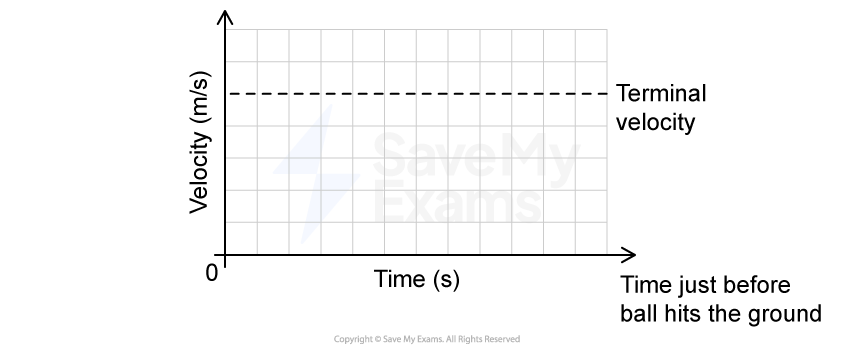
Figure 1
On the axis provided in Figure 2 sketch a displacement-time graph of the motion of the ball from the point of release to the point just before it hits the ground.
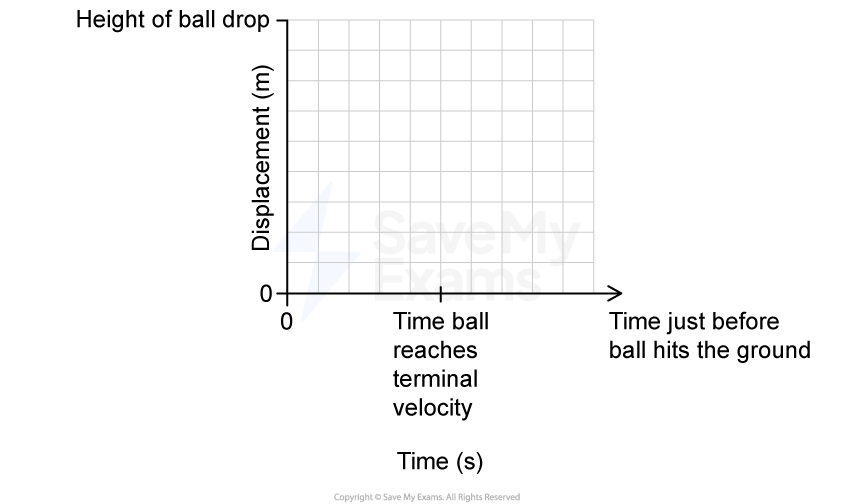
Figure 2
Figure 3 shows the free-body diagram of the forces acting on the ball during its fall. The diagram has been drawn by a student.

Figure 3
The student claims that:
"The magnitude of the forces acting on the ball are constant for the entire time the ball is falling."
Identify whether the student's claim is correct or incorrect.
⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ correct, ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ incorrect.
Justify your reasoning using Newton's second law of motion.
Did this page help you?