Calculating Work Done (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Leander Oates

Expertise

Physics

Work done equation

When an applied force displaces an object over a distance, work is done
- If a force is applied but the object is not displaced, then no work is done
For a constant force applied parallel to the displacement of the object, work is calculated using the equation:

$W = F d$

Where:
- $W$ = work, measured in $N \cdot m$
- $F$ = applied force parallel to displacement, measured in $N$
- $d$ = distance, measured in $m$
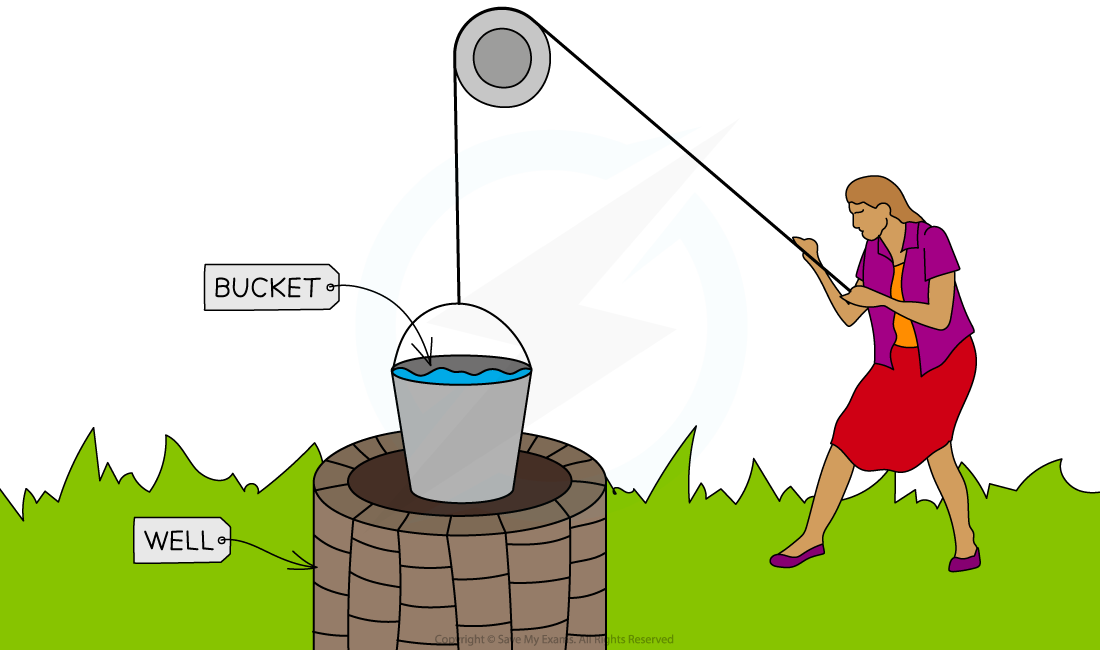
For example, if a bucket of water is raised from a well by pulling a rope with a force of $200 N$ through a height of $2 m$ , then the work done is:

$W = 200 \cdot 20 = 4000 N \cdot m$

A rope is used to lift a bucket of water from a well. Labels identify the bucket and the well. — **Work is done when a bucket of water is lifted through a height by an applied force**

Work done at an angle

Only the components of the applied force that are parallel to the displacement contribute to the work done
When a constant force is applied at an angle to the displacement of the object, work can be calculated using:

$W = F_{∥} d = F d (\cos θ)$

Where:
- $W$ = work, measured in $N \cdot m$
- $F_{∥}$ = component of the force that is parallel to the displacement of the object, measured in $N$
- $d$ = distance, measured in $m$
- $θ$ = angle at which the force is applied, measured in $°$ from the displacement vector

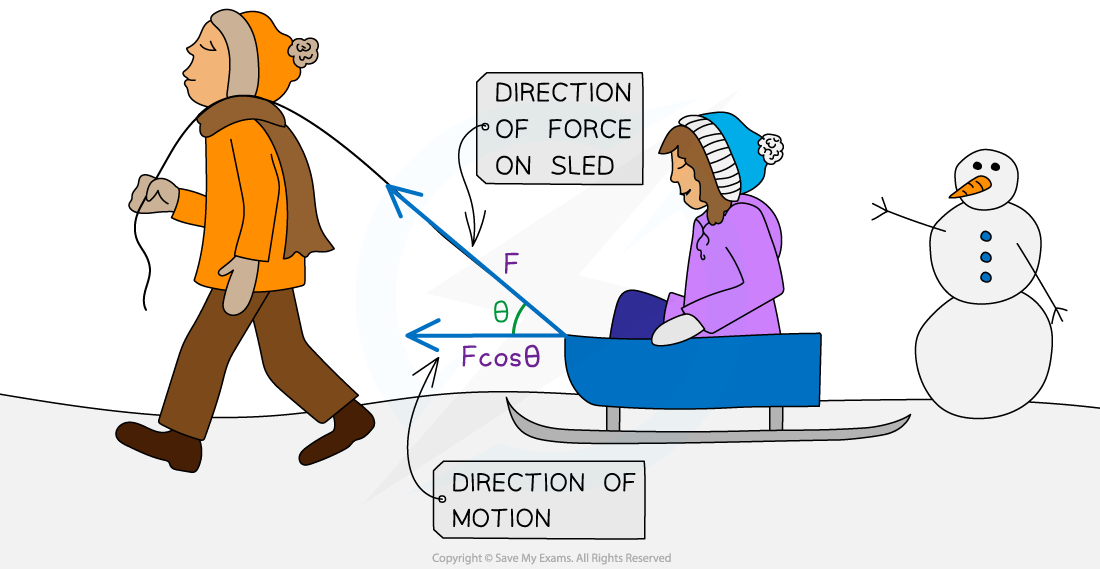
A person in winter clothes pulls a sled with another person on it. The image illustrates the direction of the applied force (F) at angle θ and Fcosθ component of that force that acts parallel to the displacement of the sled — **When a force is applied at an angle to the displacement of the object, only the component parallel to the displacement contributes to the work done**

The point of application of the force will determine the system's total energy
When the angle of the applied force is $0 \leq θ \leq 90 °$ :
- $\cos θ$ is positive
- work done is positive
- the speed of the object increases
- the kinetic energy of the object increases
When the angle of the applied force is perpendicular to the displacement, $θ = 90 °$
- $\cos θ$ is zero
- work done is zero
- the speed of the object does not change
- the kinetic energy of the object does not change
When the angle of the applied force is $90 \leq θ \leq 180 °$ :
- $\cos θ$ is negative
- work done is negative
- the speed of the object decreases
- the kinetic energy of the object decreases
When a force is applied perpendicularly to the direction of the displacement of the object, it is possible for the object to change direction without changing the kinetic energy of the object
Examples include:
- elastic collisions (detailed in the study guide on Elastic and inelastic collisions)
- circular motion (detailed in the study guide on Uniform circular motion)

Force-versus-displacement graph

If the force applied on an object is not constant, then a force-versus-displacement graph can be used to determine the work done
The force applied to an object may not always be constant
- This is more representative of real-world scenarios
In this case, the parallel component of the variable force can be plotted as a function of the displacement of the object and the work done is then equal to the area under the graph
The work done is equivalent to the area under the graph, whether there is:
- a small force applied over a large displacement
- a large force applied over a small displacement

A graph illustrating work done (in joules) with force (in newtons) on the Y-axis and displacement (in meters) on the X-axis. The area under the graph is shaded in blue. — **Graph of work done by an applied force displacing an object**

Worked Example

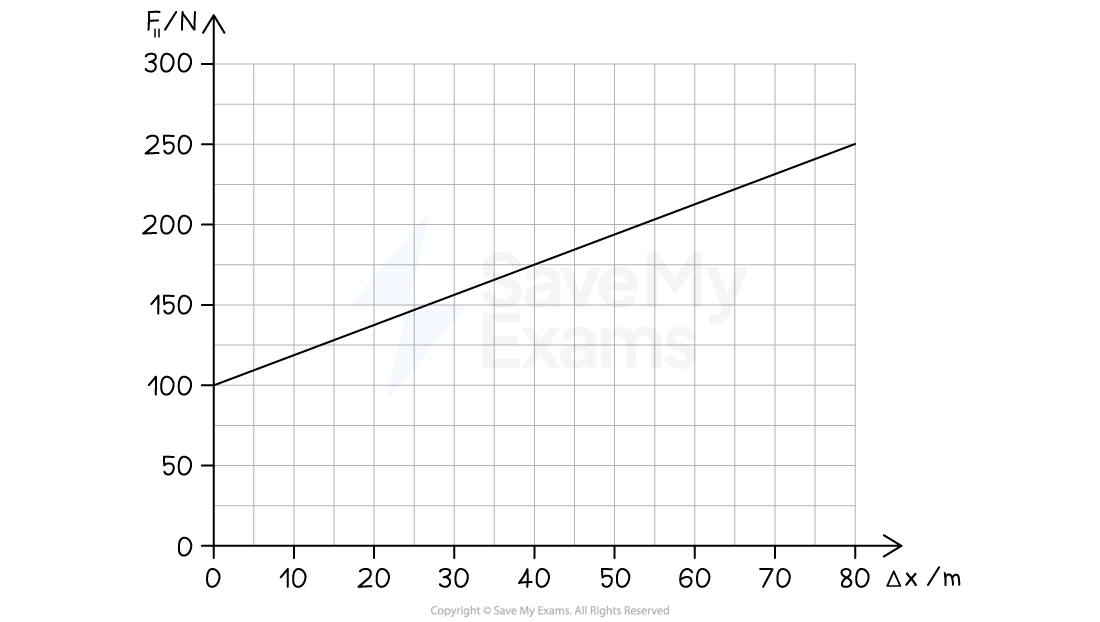
Line graph showing force as a function of displacement. A variable force acts over a distance of 80 m. The initial force applied is 100 N and increases to 250 N.

The graph above shows the parallel component of a variable force exerted on an object as a function of displacement. Which of the following is the correct value for the work done on the object?

A: $1.4 \times 10^{3} N \cdot m$

B: $6.0 \times 10^{3} N \cdot m$

C: $8.0 \times 10^{3} N \cdot m$

D: $1.4 \times 10^{4} N \cdot m$

The correct answer is D

Step 1: Split the area into sections

The area below the curve of a force-versus-displacement graph is equal to the work done
The total area is the sum of the areas of sections A and B

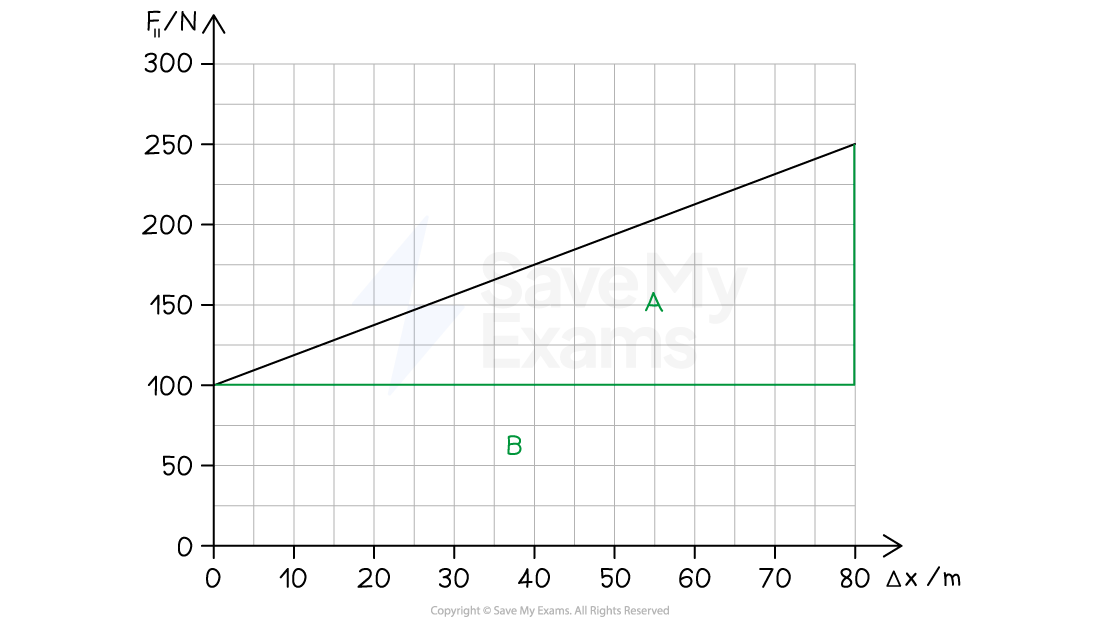
Force Displacement Graph Worked Example (2)

Step 2: Calculate the area of section A

$A_{A} = \frac{1}{2} b h$

$A_{A} = \frac{1}{2} (80) (250 - 100) = 6000 N \cdot m$

Step 3: Calculate the area of section B

$A_{B} = b h$

$A_{B} = 80 \cdot 100 = 8000 N \cdot m$

Step 4: Calculate the total work done

$W = A_{A} + A_{B}$

$W = 6000 + 8000 = 14 000 N \cdot m = 1.4 \times 10^{4} N \cdot m$

The answer is therefore D

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?