Gravitational Potential Energy Near a Surface (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Written by: Leander Oates

Reviewed by: Caroline Carroll

Gravitational potential energy near a surface

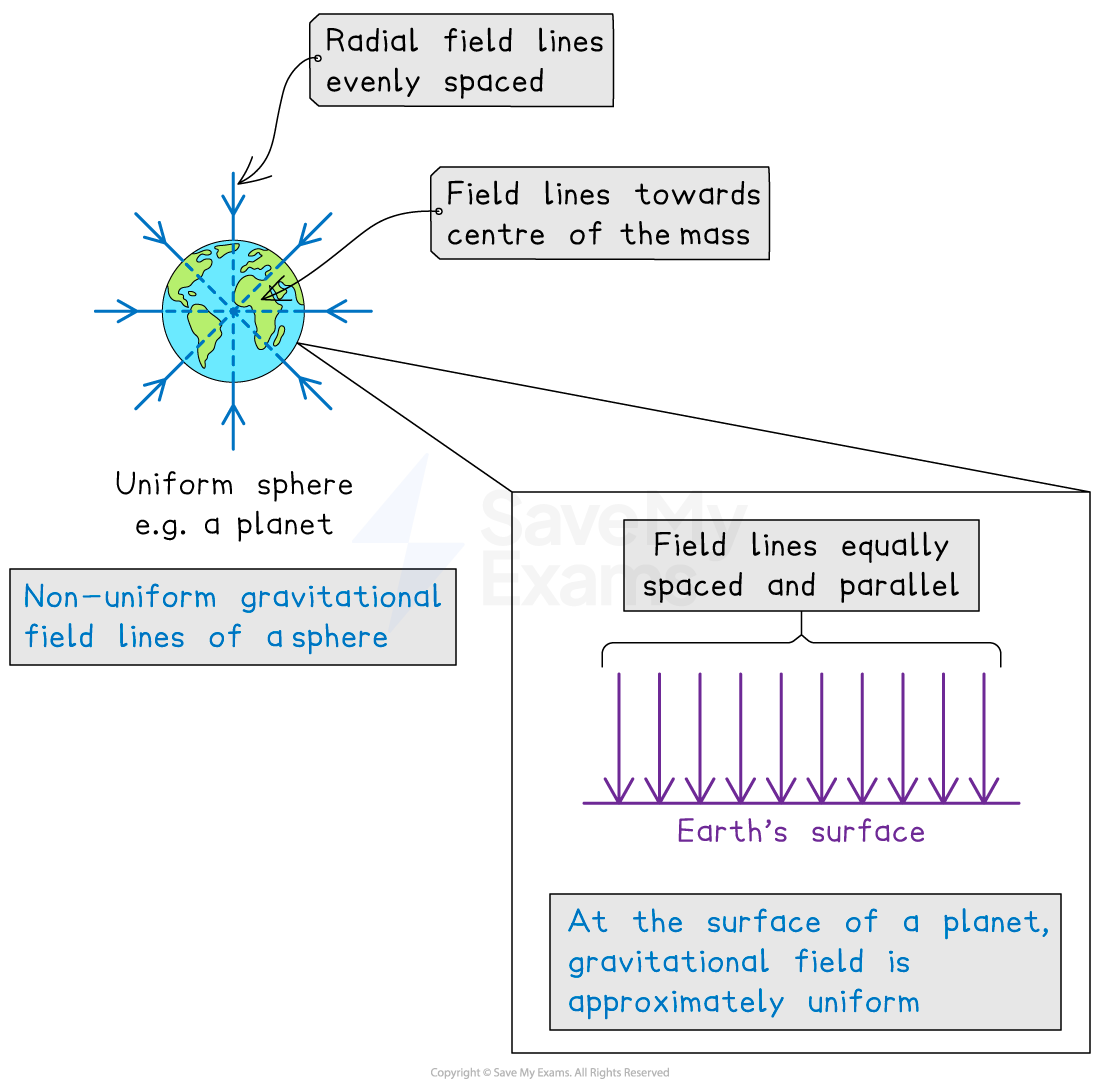
The gravitational field near the surface of a planet is nearly constant
Therefore, it can be approximated to be constant

Diagram depicting gravitational field lines around a planet. Radial field lines point towards the center, while lines near the surface are parallel and uniform. — **The gravitational field at the surface of a planet is almost uniform, therefore it can be approximated as being uniform**

The change in gravitational potential energy in a system consisting of an object near the surface of a planet and a planet, can be approximated by the equation:

$∆ U_{g} = m g ∆ y$

Where:
- $∆ U_{g}$ = change in gravitational potential energy, measured in $J$
- $m$ = mass of object moving through a gravitational field, measured in $kg$
- $g$ = gravitational field strength of planet, measured in $N / kg$
- $∆ y$ = vertical distance moved by object through a gravitational field, measured in $m$
This equation assumes that the gravitational field through which the object moves is constant
The gravitational potential energy and the height through which the object is moved are relative
- The zero points of potential energy and displacement are adjusted based on the situation (this is covered in greater detail in the study guide on potential energy)
- This is shown by the $∆$ (delta) symbol, meaning change in
When an object is lifted through a gravitational field, the system gains gravitational potential energy
When an object is lowered through a gravitational field, the system loses gravitational potential energy

Diagram showing an object thrown in the air and an object falling, with corresponding graphs of gravitational potential energy (GPE) against height for each scenario. — **Graphs showing the linear relationship between gravitational potential energy and height**

The gravitational force is a conservative force; therefore, gravitational potential energy is path-independent
- This is covered in greater detail in the study guide, Potential Energy
Gravitational potential energy is a scalar quantity with magnitude only

Worked Example

A rock of mass $2.1 kg$ is dropped from a cliff into the water $12 m$ below. The person that drops the rock releases it from a height of $1.4 m$ above the ground. Which of the following values is correct for the speed of the rock just before it hits the water?

A: $6.5 m / s$

B: $14.5 m / s$

C: $15.5 m / s$

D: $16.4 m / s$

The correct answer is D

Step 1: Analyze the scenario

The cliff is $12 m$ above the water, but the rock is dropped from a height of $1.4 m$ above the ground; therefore, the total vertical distance the rock travels is $12 + 1.4 = 13.4 m$
Air resistance is always assumed to be negligible unless otherwise stated
Therefore, it can be assumed that the gravitational potential energy is transformed into kinetic energy with 100% efficiency

Step 2: List the known quantities

Mass of rock, $m = 2.1 kg$
Vertical distance traveled by rock, $∆ y = 13.4 m$
Magnitude of the gravitational field strength at the Earth's surface, $g = 10 N / kg$

Step 3: Calculate the change in gravitational potential energy as the rock falls to the surface of the water

$∆ U_{g} = m g ∆ y$

$∆ U_{g} = 2.1 \cdot 10 \cdot 13.4 = 281.4 J$

Step 4: Equate the change in gravitational potential energy to the gain in kinetic energy

$∆ U_{g} = K = \frac{1}{2} m v^{2}$

Step 5: Rearrange to make speed the subject and substitute in the known values to calculate

$∆ U_{g} = \frac{1}{2} m v^{2} \Rightarrow v = \sqrt{\frac{2 \cdot ∆ U_{g}}{m}}$

$v = \sqrt{\frac{2 \cdot 281.4}{2.1}} = 16.4 m / s$

Examiner Tips and Tricks

You could also solve this problem by equating the expressions for gravitational potential energy and translational kinetic energy:

$m g ∆ y = \frac{1}{2} m v^{2}$

$g ∆ y = \frac{1}{2} v^{2}$

$v = \sqrt{2 g ∆ y}$

Last updated: 19 October 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Elastic Potential EnergyNext:Gravitational Potential Energy Between Objects