Defining Torque (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Katie M

Expertise

Physics

What is torque?

Torque is the rotational analog of force
In the same way that a net force causes linear acceleration, a net torque causes angular acceleration
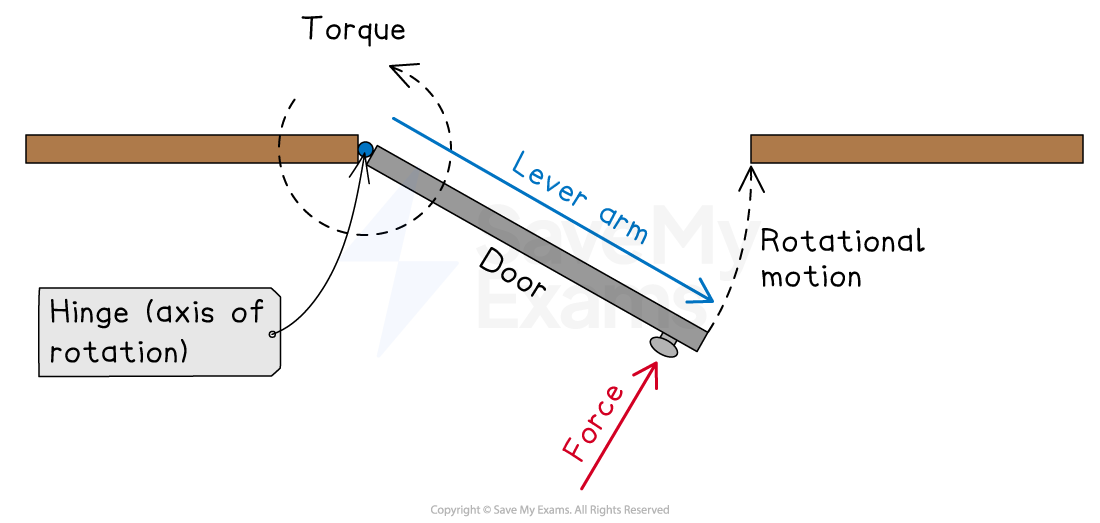
A torque is produced when a force is applied at a distance from an axis of rotation and causes a change in rotational motion
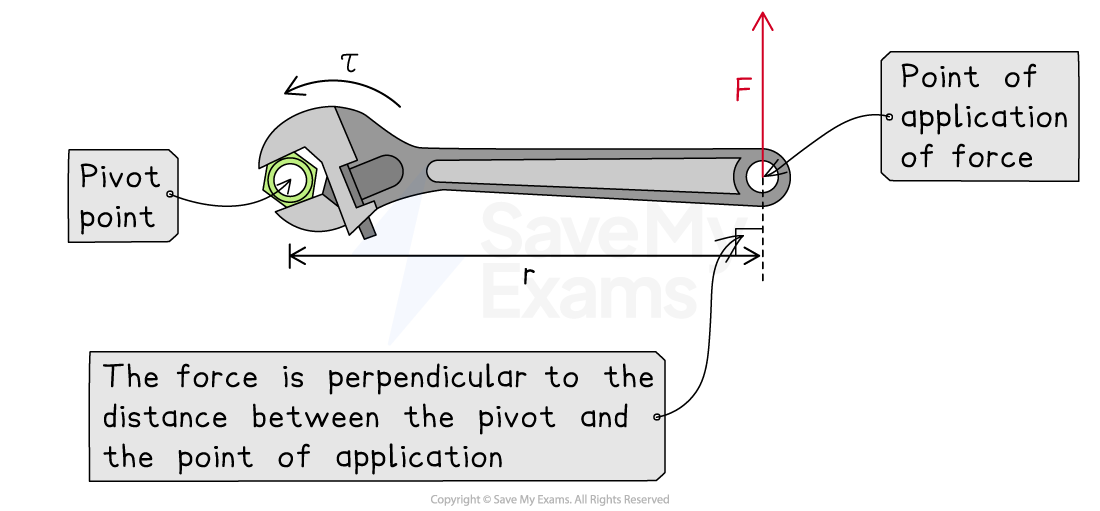
- The component of the force that causes the torque is perpendicular to the lever
- The perpendicular distance from the axis of rotation to the line of action of the force is called the lever arm
This means that a force applied at the pivot, or axis of rotation, will not produce a torque

Torque exerted on a closing door

Diagram depicting a door being closed with labeled parts: hinge (axis of rotation), door, lever arm, applied force (red arrow), torque (curved arrow), and rotational motion. — **When a force is applied to a lever (e.g. a door), a torque is exerted about the axis of rotation (i.e. the door's hinge)**

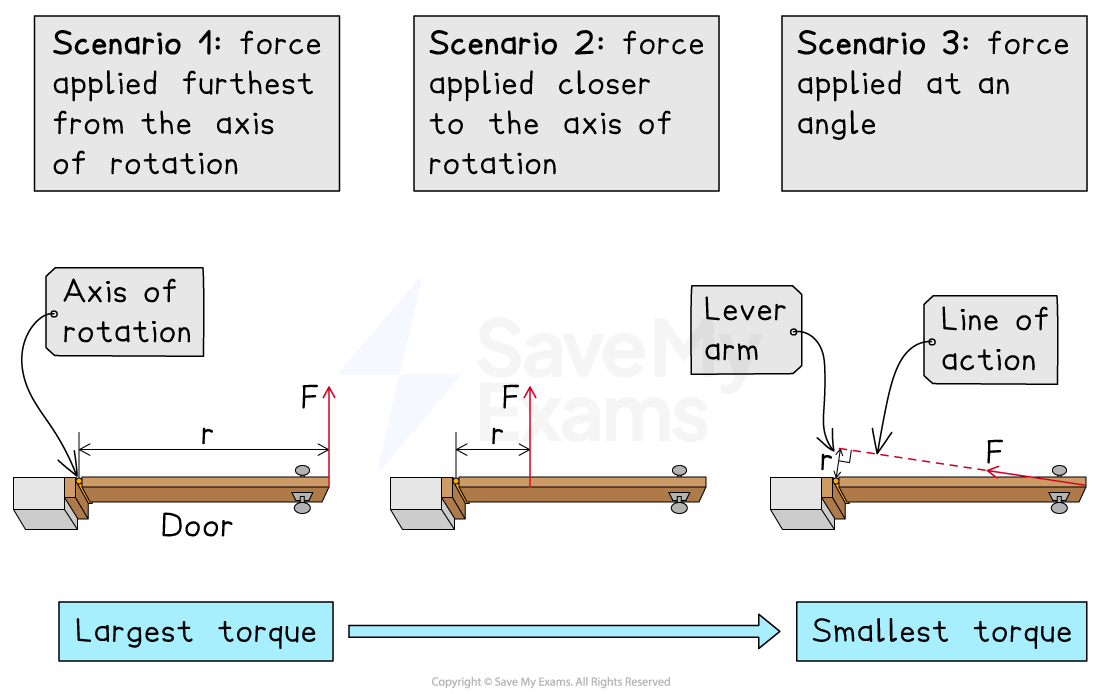
The magnitude of a torque depends on
- the magnitude of the applied force
- the distance from the axis of rotation to the point of application of the force
- the angle between the position vector and the force vector

Diagram showing three scenarios of force applied to a door with varying distances and angles from the axis of rotation to illustrate torque. — **The largest magnitude of torque is produced when a force is applied furthest from the axis of rotation and perpendicular to the lever**

Torque equation

Torque can be defined as:

The product of the force and the perpendicular distance from the axis of rotation (lever arm)

The magnitude of the torque exerted on a rigid system by a force is:

$τ = r F_{⊥} = r F \sin θ$

Where:
- $τ$ = magnitude of the torque, in $N \cdot m$
- $F_{⊥}$ = the component of the force that is perpendicular to the lever arm
- $F$ = magnitude of the applied force, in $N$
- $r$ = lever arm, in $m$
- $θ$ = angle between the applied force and the lever arm in $°$

Torque of a perpendicular force

Diagram of a spanner illustrating torque, showing pivot point, applied force direction, distance from pivot to force, and perpendicular force application. — **A maximum torque is produced when a force applied is at right angles to the distance between the pivot and the point of application of the force.**

Torque of a non-perpendicular force

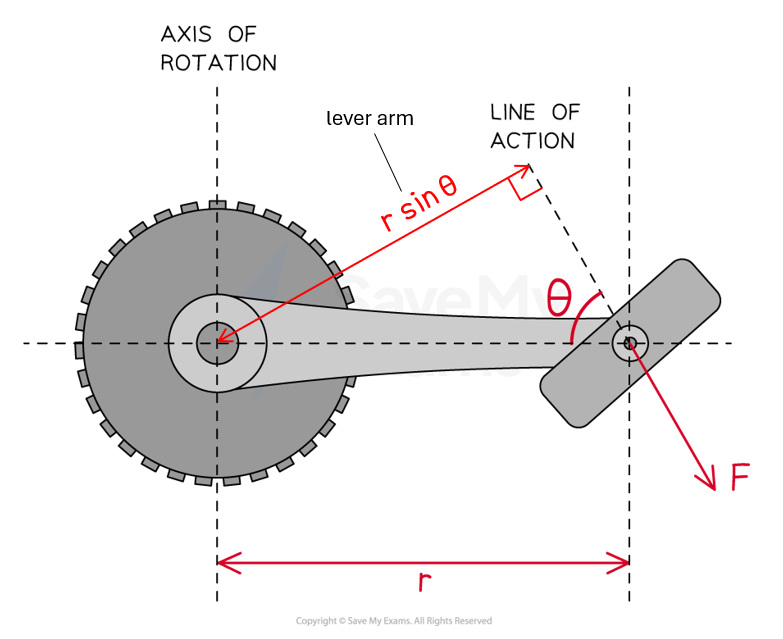
Diagram of a bicycle pedal rotating around an axis, with labeled parts: axis of rotation, line of action, force (F), radius (r), and angle (θ) between force and arm of the mechanism. — The torque applied by a cyclist on a bicycle pedal is equal to the product of the applied force F and the perpendicular distance between the line of action of the force and the axis of rotation r sin θ

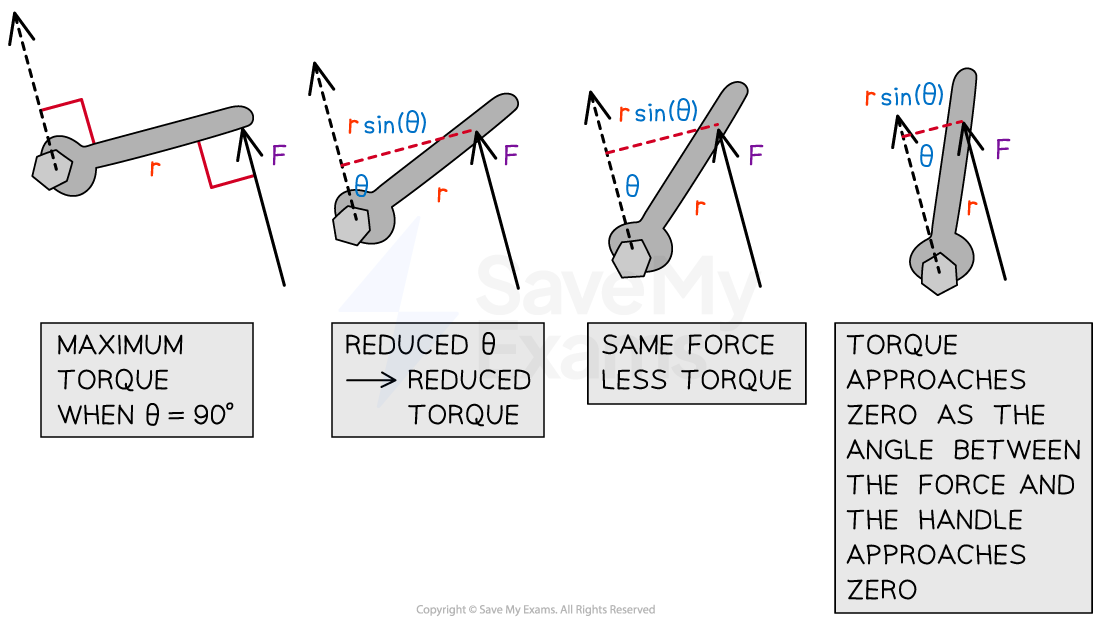
The maximum torque that can be exerted on a rigid system is when the force is perpendicular $(θ = 90 °)$ to the lever arm

$τ = F r$

As a result, the same force is less effective when applied at non-perpendicular angles

Effect of angle on torque

Diagram showing the relationship between force, angle, and torque on a wrench. As the angle decreases from 90 degrees, torque reduces, eventually approaching zero. — **The force produces a maximum torque when applied perpendicular to the arm of the wrench. The same force is less effective when applied at non-perpendicular angles**

Worked Example

The forces acting on a bicycle pedal at different positions during a ride are shown in the diagram below. The distance from the pedal to the axis of rotation is 24 cm.

In which of the following positions is the magnitude of the torque the greatest?

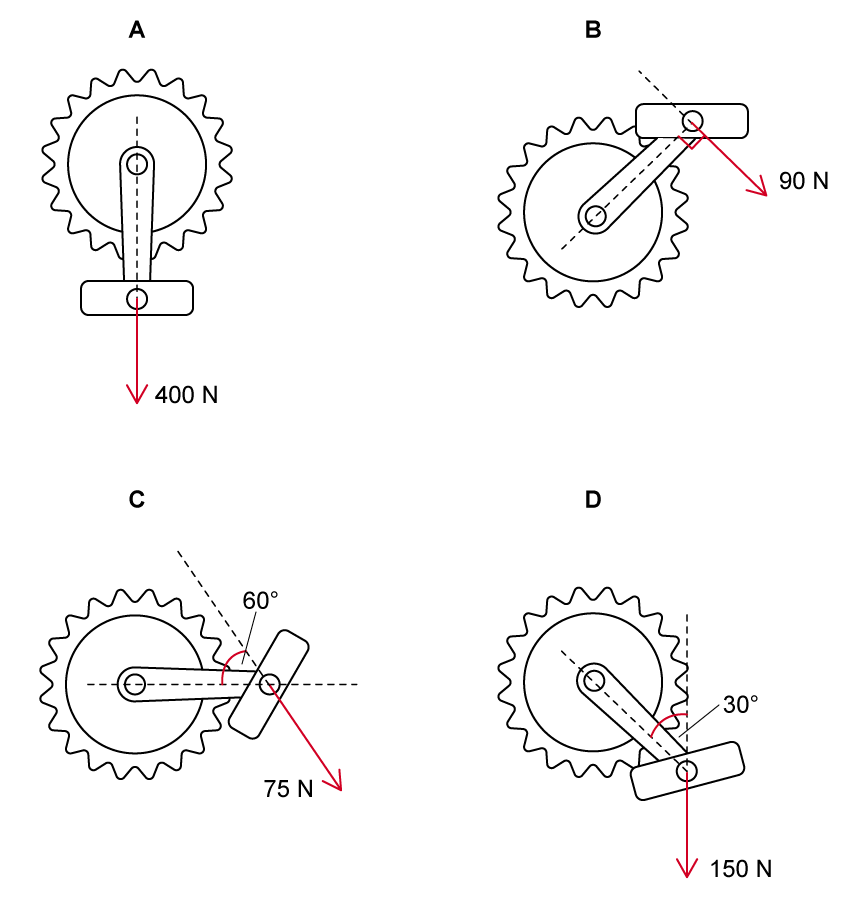
Diagrams A, B, C, and D show gears with varying forces (400 N, 90 N, 75 N, 150 N) applied at different angles (60°, 30°) to the attached levers.

The correct answer is B

Answer:

Step 1: Analyze the scenario

The magnitude of torque on a rigid system is:

$τ = F r \sin θ$

The maximum torque is exerted when $θ = 90 °$ , where $θ$ is the angle between the line of action of the force and the lever arm
In each case, the lever arm is the same, $r$ = 24 cm = 0.24 m

Step 2: Eliminate incorrect options

In position A: $F$ = 400 N and $θ$ = 180°, so:

$τ = 400 \times \sin 180 ° = 400 \times 0 = 0$

This means when the component of force is parallel to the lever arm, no torque is exerted on the pedal
Therefore, when the pedal is in this position, no amount of pushing down will produce any change in its rotational motion

Step 3: Deduce the correct answer

In position B: $F$ = 90 N and $θ$ = 90°, so:

$τ = 0.24 \times 90 \times \sin 90 = 21.6 N \cdot m$

In position C: $F$ = 75 N and $θ$ = 60°, so:

$τ = 0.24 \times 75 \times \sin 60 = 15.6 N \cdot m$

In position D: $F$ = 150 N and $θ$ = 30°, so:

$τ = 0.24 \times 150 \times \sin 30 = 18.0 N \cdot m$

The largest torque occurs in position B

Examiner Tip

You should know that torque is a vector quantity, however, in the AP Physics 1 exam, you will only need to consider whether it produces clockwise or anti-clockwise motion, and then use vector conventions to calculate the magnitude of torque accordingly. The direction of torque is beyond the scope of the course and will not be tested.

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?