Connecting Linear & Rotational Motion (College Board AP® Physics 1: Algebra-Based)

Study Guide

Written by: Katie M

Connecting linear & rotational motion

The rotational quantities that describe a point on a rotating rigid body can be related to their corresponding linear quantities

Summary of linear and angular variables

variable	linear variable	angular variable
displacement	$s$	$θ$
velocity	$v$	$ω$
acceleration	$a$	$α$

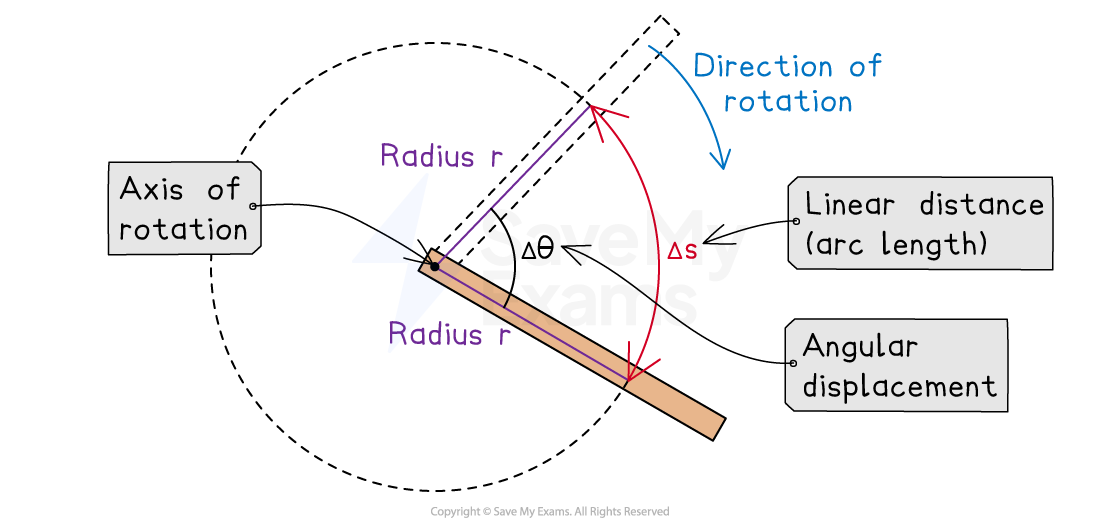
Linear and angular displacement

For a point on a rigid system that rotates about a fixed axis of rotation, the linear distance traveled by the point is given by:

$∆ s = r ∆ θ$

Where:
- $∆ s$ = linear distance traveled by the point, in $m$
- $∆ θ$ = angular displacement of the point, in $rad$
- $r$ = distance from a fixed axis of rotation, in $m$

Diagram showing rotational motion with labeled elements: axis of rotation, radius (r), angular displacement (Δθ), linear distance (arc length Δs), and direction of rotation. — **Using the definition of a radian, the linear distance s traveled by a point on a rotating rigid system can be related to the angular displacement Δθ**

Linear and angular velocity

The linear velocity of a point on a rotating rigid body is equal to the linear distance traveled by the point divided by the time $∆ t$

$v = \frac{∆ s}{∆ t} = \frac{r ∆ θ}{∆ t}$

The angular velocity of the system is equal to the rate of change of angular displacement

$ω = \frac{∆ θ}{∆ t}$

Therefore, the linear speed of a point is related to the angular speed of the system by the equation:

$v = r ω$

Where:
- $v$ = linear speed of a point, in $m / s$
- $ω$ = angular speed of the system, in $rad / s$
- $r$ = distance from a fixed axis of rotation, in $m$
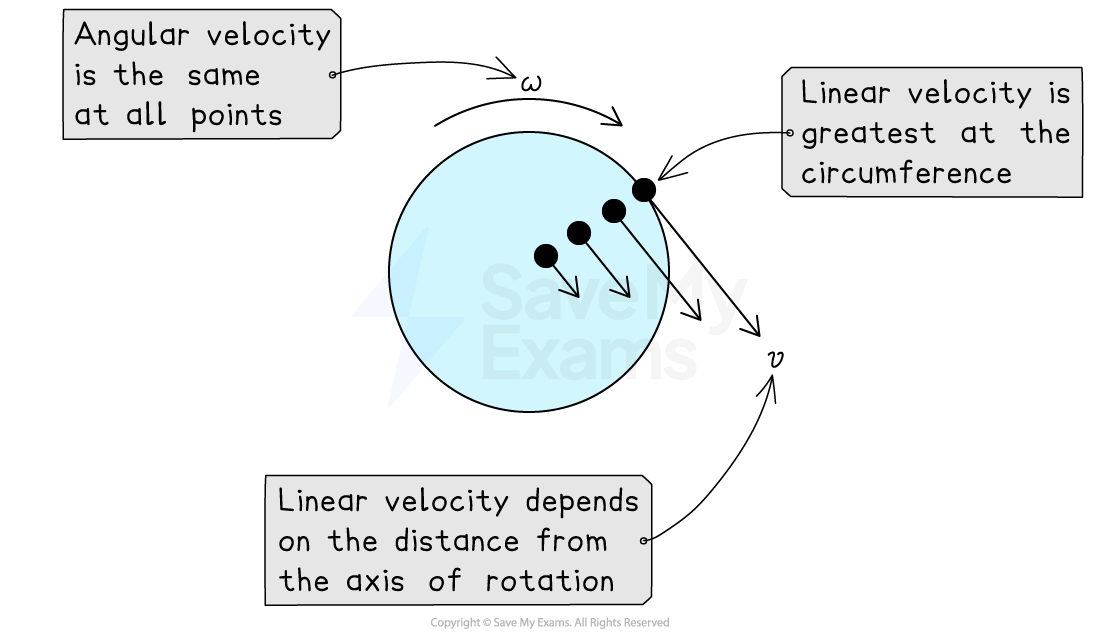
For a rigid system, all points within that system have the same angular velocity
- However, not all points have the same linear velocity
The relationship above tells us the linear velocity of a point:
- increases with distance from the axis of rotation
- has a maximum value at the radius of the system
- is zero at the axis of rotation
The linear velocity of a point on a rigid rotating body is also known as its tangential velocity
- This is because the instantaneous direction of the velocity is always at a tangent to the direction of rotation

Diagram of a rotating circle showing angular velocity (ω) as constant. Linear velocity (v) varies with distance from the axis, greatest at the circumference. — **All points on the rigid object will have the same angular velocity, but not the same linear velocity**

Linear and angular acceleration

The tangential acceleration of a point on a rotating rigid body is equal to the rate of change of linear velocity at that point

$a_{T} = \frac{∆ v}{∆ t} = \frac{r ∆ ω}{∆ t}$

The angular acceleration of the system is equal to the rate of change of angular velocity

$α = \frac{∆ ω}{∆ t}$

Therefore, the tangential acceleration of a point is related to the angular acceleration of the system by the equation:

$a_{T} = r α$

Where:
- $a_{T}$ = tangential acceleration of a point, in $m / s^{2}$
- $α$ = angular acceleration of the system, in $rad / s^{2}$
- $r$ = distance from a fixed axis of rotation, in $m$
For a rigid system, all points within that system have the same angular acceleration

Examiner Tips and Tricks

While there are many similarities between the angular quantities used in this topic and the angular quantities used in the circular motion topic, make sure you are clear on the distinctions between the two, for example, angular acceleration and centripetal acceleration are not the same thing!

Last updated: 19 October 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Angular AccelerationNext:Rotational Kinematics Equations