AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 5: Torque & Rotational DynamicsRotational KinematicsAngular Displacement

Angular Displacement (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself
Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Angular displacement

Angular position

  • Angular position is defined as:

The rotational location (angle) of a point on a rigid system, relative to a reference point

  • In linear motion, the position of an object is measured relative to the origin of a coordinate system

  • In rotational motion, the angular position of a point on a rigid system is measured relative to the axis of rotation

Diagram of a circle representing a rotating system with an axis at O. Labels indicate position vector, radius, point on the rotating system, angular position, arc length, and direction of rotation.
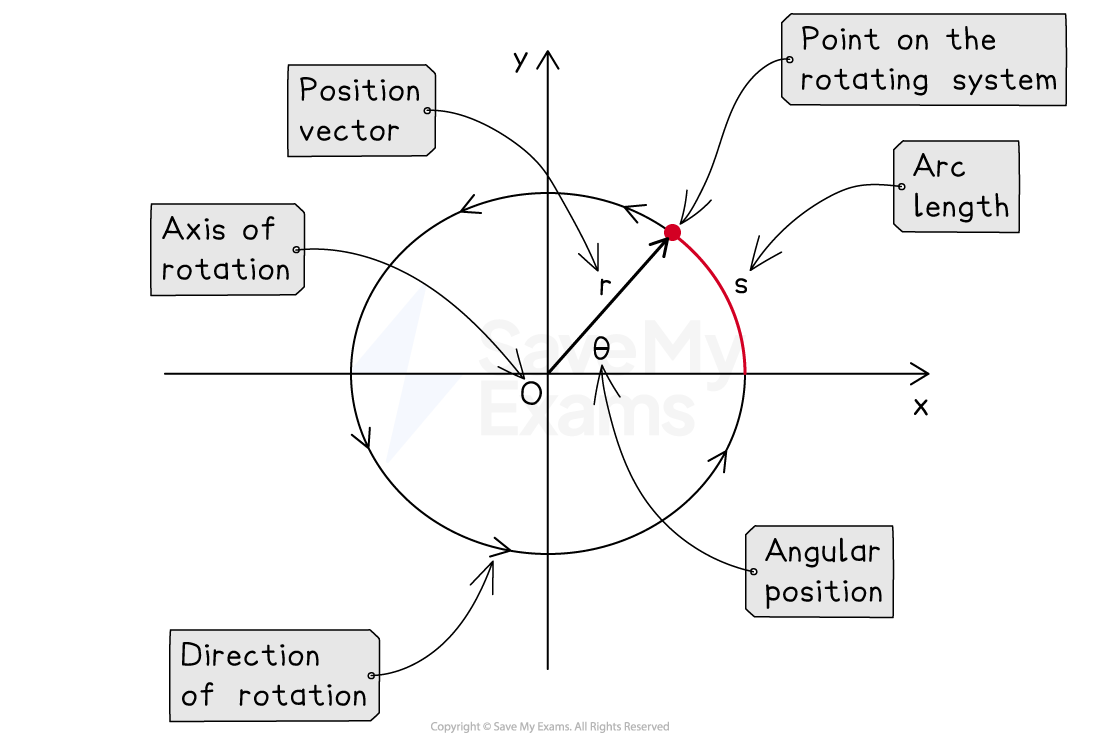
The angular position of a point on a rigid system is measured relative to the axis of rotation, which is the horizontal x-axis. As the point moves along its circular path, the position vector r sweeps out an angle θ, which increases in the counterclockwise direction.

  • The angular position of a point on a rigid system theta is measured relative to a reference line

  • As the point moves, the only quantity that changes is theta

  • The reference line could be a coordinate plane or another position vector

    • For example, point A is at an angle of 30° with respect to the x-axis

    • Or, point P on an extended rigid object rotates clockwise by 75° with respect to its initial position vector

Rotation of an extended object about a fixed reference axis

Diagram showing a circular motion with points P at initial and final positions, connected to a fixed reference axis O, illustrating angular position θ.
When a rigid, extended object rotates about an axis through the point O, its angular position is described by the angle through which a point P has rotated about that axis relative to a fixed reference axis

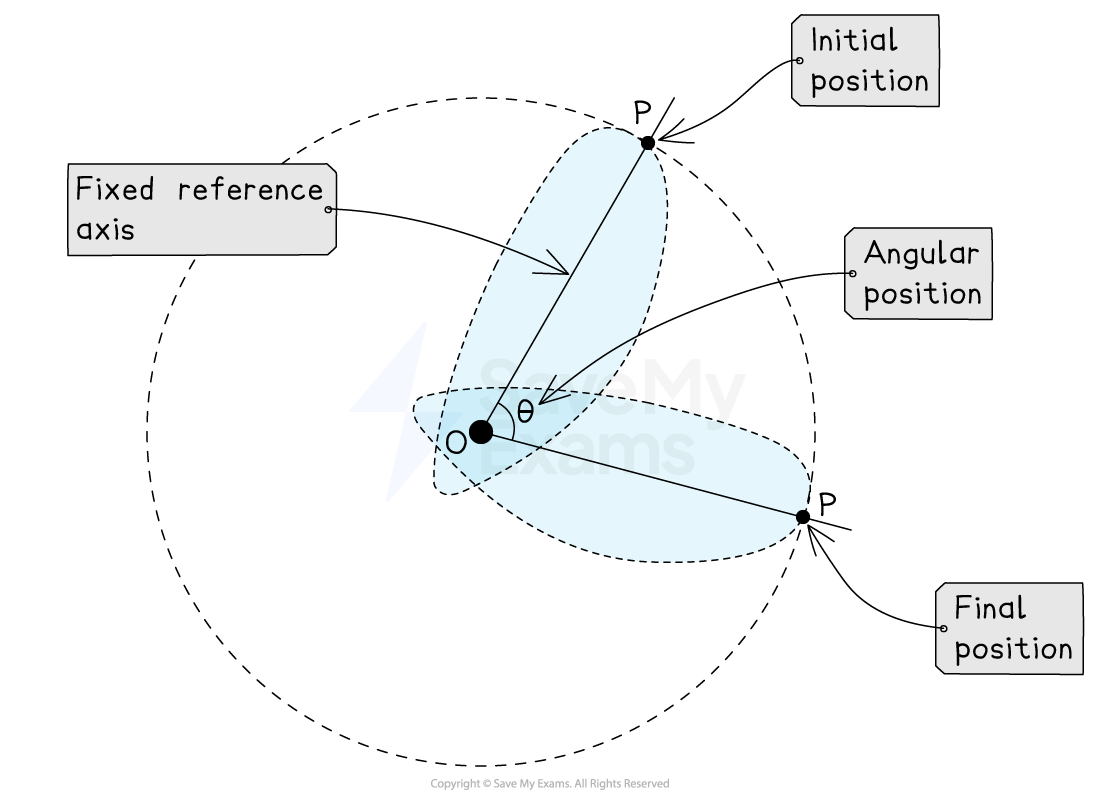
  • The relative nature of a point's angular position gives it a directional component

  • As a result, angular position is a vector quantity with both magnitude and direction

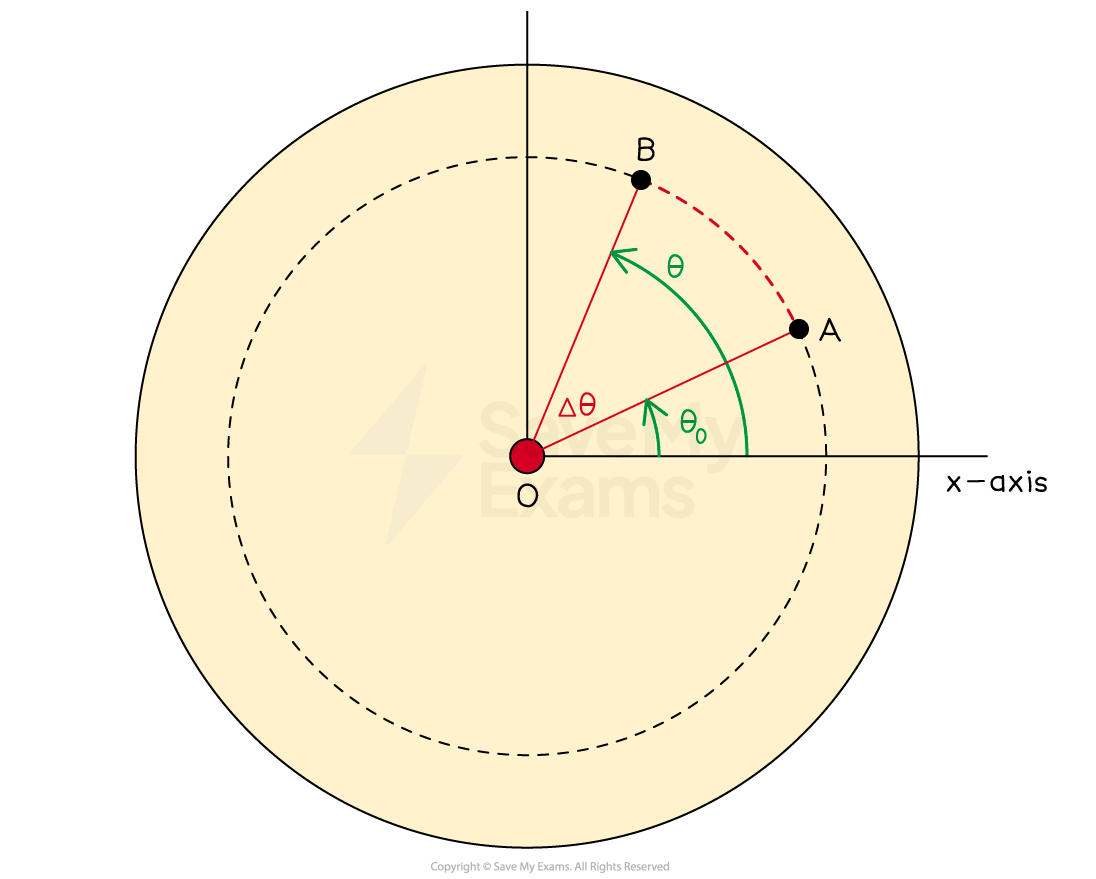
Angular displacement

  • Angular displacement is defined as:

The change in angle through which a point on a rigid system rotates about a specified axis

  • The angular displacement of a rotating rigid system describes the difference in angular position between a point's starting position vector and its finishing position vector

  • This can be described by the equation:

increment theta space equals space theta space minus space theta subscript 0

  • Where:

    • increment theta = angular displacement, in rad

    • theta = final angular position, in rad

    • theta subscript 0 = initial angular position, in rad

Defining angular displacement

Diagram of a circle with center O. Points A and B are on the circle's circumference. A red angle Δθ, green angles θ0, and θ are shown. The x-axis is labeled.
When a point on a rotating rigid body moves from initial position A to final position B, the angular displacement Δθ is equal to the difference between the initial and final angular positions

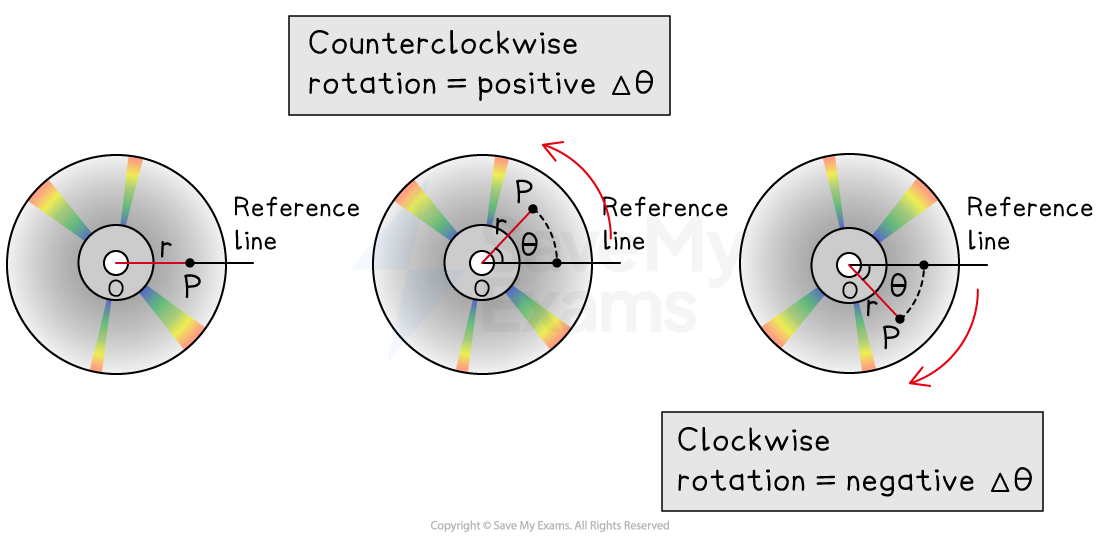
Direction of angular displacement

  • Like linear displacement, angular displacement is a vector quantity with both magnitude and direction

    • The direction of a system's angular displacement can be described as clockwise or counterclockwise with respect to a given axis of rotation

    • Mathematically, either direction can be assigned as positive only if the opposing direction is negative

  • For example, consider a disc rotating about an axis of rotation at its center, where counterclockwise is defined as the positive direction

    • If the disc rotates counterclockwise, its angular displacement is positive

    • If the disc rotates clockwise, its angular displacement is negative

Three diagrams showing rotation of a disc with a reference line. Left: point P; center: counterclockwise path is positive θ; right: clockwise path is negative θ.
If counterclockwise is defined as the positive direction, then when the disc rotates counterclockwise, its angular displacement relative to the reference line is positive, and negative when it rotates clockwise

Units of angular displacement

  • Angular displacement is measured in radians

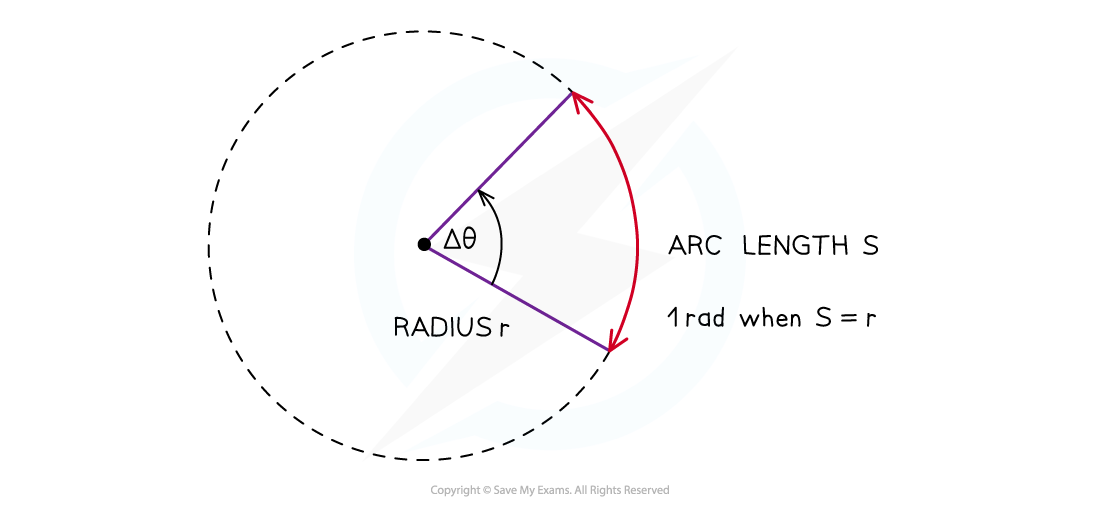
  • A radian, or rad, is defined as:

The angle subtended at the center of a circle by an arc equal in length to the radius of the circle

  • It can be expressed as:

theta space equals space s over r

  • Where:

    • theta = angle subtended from the center of the circle, in rad

    • s = arc length, in straight m

    • r = radius of the circle, in straight m

Definition of a radian

Illustration showing a circle with radius r, an angle Δθ, and an arc length S. It states "1 rad when S = r" indicating radians measurement.
When the angle is equal to one radian, the length of the arc (S) is equal to the radius (r) of the circle

  • Any angle in degrees can be converted into radians using the equation:

theta open parentheses rad close parentheses space equals space theta open parentheses degree close parentheses cross times fraction numerator straight pi over denominator 180 degree end fraction

  • Radians are commonly written in terms of π, where:

    • 360° is equivalent to 2 straight pi

    • 270° is equivalent to fraction numerator 3 straight pi over denominator 2 end fraction

    • 180° is equivalent to straight pi

    • 90° is equivalent to straight pi over 2

Examiner Tips and Tricks

You should be aware that a radian is not technically a unit. It is a dimensionless ratio, as the units of arc length and radius cancel. This means that an angle described in radians has no unit and does not need to be converted from one unit to another. However, we often write “rad” after an angle measured in radians to remind ourselves that the quantity describes an angle.

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Rotating SystemsNext:Angular Velocity
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.