Study GuidesExam QuestionsPast Papers
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 5: Torque & Rotational DynamicsRotational InertiaParallel Axis Theorem

Parallel Axis Theorem (College Board AP® Physics 1: Algebra-Based): Study Guide

Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on

Parallel axis theorem

  • The rotational inertia of a rigid system can change depending on the orientation of its rotational axis

    • The minimum rotational inertia in any plane is always about the axis which passes through the system's center of mass

  • A rigid system may not always rotate about an axis passing through its center of mass

    • As a result, the rotational inertia will always be greater than if the axis passed through the system's center of mass

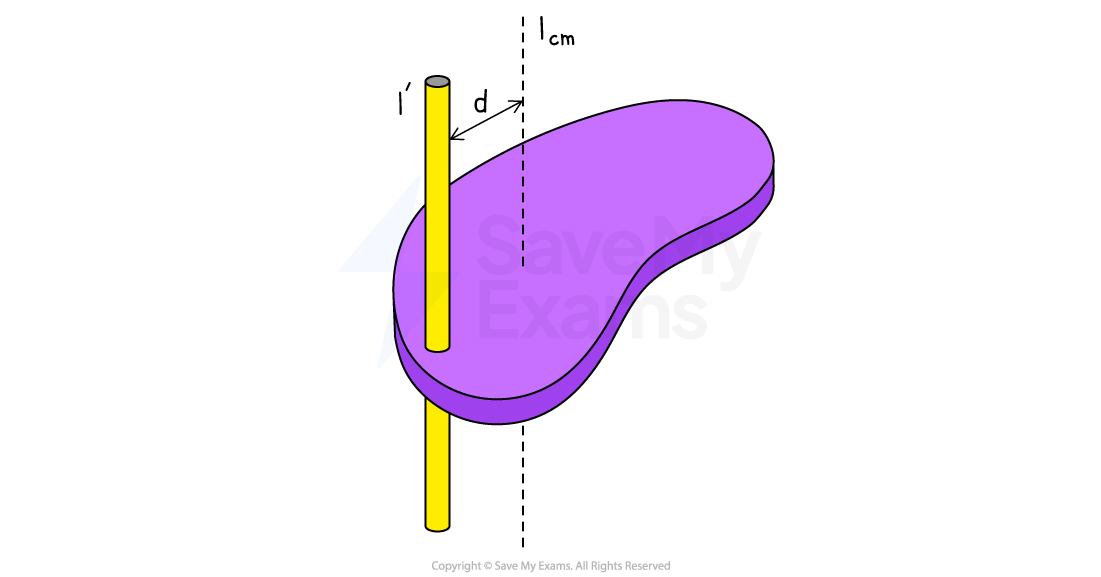
  • The rotational inertia about an axis that is parallel to an axis passing through the center of mass can be calculated using the parallel axis theorem

I apostrophe space equals space I subscript c m end subscript space plus thin space M d squared

  • Where:

    • I subscript c m end subscript = rotational inertia about an axis passing through the system’s center of mass

    • I apostrophe = rotational inertia about an axis parallel to I subscript c m end subscript

    • M = mass of the system, in kg

    • d = distance between the rotational axis and the system’s center of mass

  • This means that the rotational inertia of a system will be the same when rotating about any parallel axis at an equal distance from the center of mass

Rotational inertia around a parallel axis

Diagram showing an irregular shaped object with a yellow cylindrical rod which is parallel to its center of mass. Variables I', Icm, and d indicate distances and axes.
The rotational inertia about another axis that is parallel to the axis through the center of mass, at a distance d from the object’s center of mass, can be determined using the parallel axis theorem

Worked Example

The rotational inertia of a rod of mass M and length Lrotating about its center of mass is 1 over 12 M L squared. Which of the following describes the rotational inertia of the rod rotating about one of its ends?

A 1 half M L squared

B 1 third M L squared

C 1 over 6 M L squared

D 1 over 12 M L squared

The correct answer is B

Answer:

Step 1: Determine the distance between the center of mass and the parallel axis

d space equals space L over 2

Step 2: Apply the parallel axis theorem to the rod

I apostrophe space equals space I subscript c m end subscript space plus thin space M d squared

I apostrophe space equals space 1 over 12 M L squared space plus space M open parentheses L over 2 close parentheses squared

I apostrophe space equals space 1 over 12 M L squared space plus space 1 fourth M L squared

I apostrophe space equals space 1 third M L squared

Worked Example

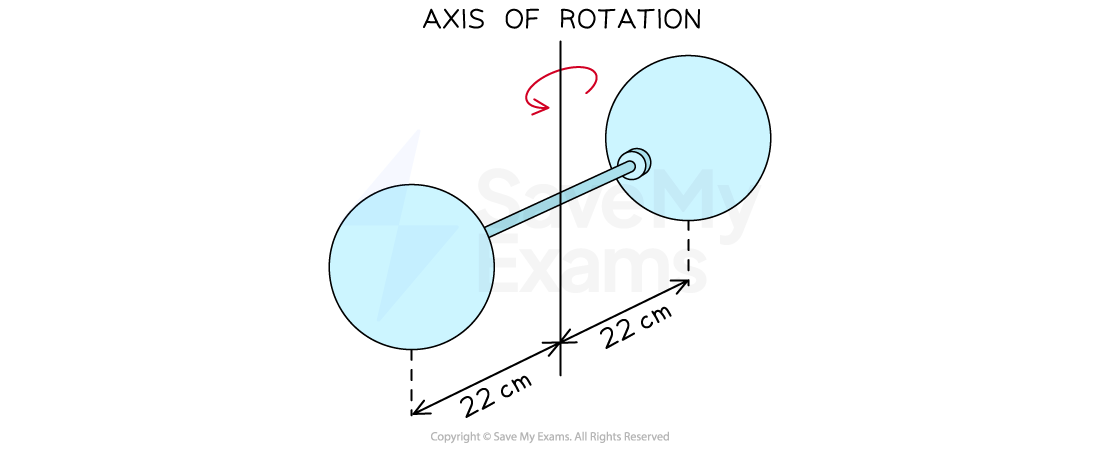
Two solid spheres form a dumbbell when attached to each end of a thin uniform rod. The dumbbell rotates with the center of mass of each sphere at a distance of 22 cm from the axis of rotation, as shown in the diagram.

The rod has a mass of 150 g. Each sphere has a radius of 4 cm and a mass of 750 g.

Diagram of a barbell with two weights, each 22 cm from the central axis of rotation. The barbell rotates around the center with an indicated red arrow.

Rotational inertia of a thin rod about its center = 1 over 12 m L squared

Rotational inertia of a solid sphere about its center = 2 over 5 M R squared

(A) Calculate the total rotational inertia of the dumbbell arrangement

(B) Determine the proportion of rotational inertia the thin rod contributes to the dumbbell arrangement

Answer:

Part (A)

Step 1: Analyze the scenario

  • The total rotational inertia of the dumbbell is the sum of

    • the rotational inertia of each solid sphere about the center of the rod

    • the rotational inertia of the thin rod about its center

Step 2: Calculate the rotational inertia of each sphere

  • The rotational inertia of a solid sphere about its own center of mass is I subscript s p h e r e comma c m end subscript space equals space 2 over 5 M R squared

  • The rotational inertia of each sphere about the center of the rod can be found using the parallel axis theorem

I subscript s p h e r e end subscript space equals space I subscript s p h e r e comma c m end subscript space plus space M d squared

  • The mass of each sphere is M space equals space 750 space straight g space equals space 0.75 space kg

  • The radius of each sphere is R space equals space 4 space cm space equals space 0.04 space straight m

  • The distance between the rotational axis and each sphere is d space equals space 22 space cm space equals space 0.22 space straight m

I subscript s p h e r e end subscript space equals space 2 over 5 M R squared space plus thin space M d squared

I subscript s p h e r e end subscript space equals space 2 over 5 open parentheses 0.75 close parentheses open parentheses 0.04 close parentheses squared space plus space open parentheses 0.75 close parentheses open parentheses 0.22 close parentheses squared space equals space 0.0368 space kg times straight m squared

Step 3: Calculate the rotational inertia of the rod

  • The mass of the rod is m space equals space 150 space straight g space equals space 0.15 space kg

  • The length of the rod is L space equals space 2 cross times open parentheses 22 minus 4 close parentheses space equals space 36 space cm space equals space 0.36 space straight m

I subscript r o d end subscript space equals space 1 over 12 m L squared

I subscript r o d end subscript space equals space 1 over 12 open parentheses 0.15 close parentheses open parentheses 0.36 close parentheses squared space equals space 0.00162 space kg times straight m squared

Step 4: Calculate the total rotational inertia of the system

I subscript t o t end subscript space equals space sum m r squared

I subscript t o t end subscript space equals space 2 I subscript s p h e r e end subscript space plus space I subscript r o d end subscript

I subscript t o t end subscript space equals space 2 open parentheses 0.0368 close parentheses space plus space 0.00162 space equals space 0.0752 space kg times straight m squared

Part (B)

Step 1: Analyze the scenario

  • The proportion of rotational inertia contributed by the thin rod is given by

I subscript r o d end subscript over I subscript t o t end subscript

Step 2: Calculate the ratio of the rotational inertias

I subscript r o d end subscript over I subscript t o t end subscript space equals space fraction numerator 0.00162 over denominator 0.0752 end fraction space equals space 0.0215 space almost equal to space 2 percent sign

  • This means the rod contributes about 2% of the overall rotational inertia of the dumbbell

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Rotational InertiaNext:Rotational Equilibrium
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.