AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 5: Torque & Rotational DynamicsNewton’s First & Second Law in Rotational FormRotational Equilibrium

Rotational Equilibrium (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself
Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Rotational equilibrium

  • Rotational equilibrium is defined as

A configuration of torques such that the net torque exerted on the system is zero

  • This can be expressed as:

sum tau subscript i space equals space 0

  • Rotational equilibrium is analogous to translational equilibrium

  • For a system in rotational equilibrium

    • no net torque acts on it

    • it has zero angular acceleration

    • it remains at rest or rotates with a constant angular velocity

Balanced torque

  • When a system is in rotational equilibrium, this means that

The sum of the clockwise torques is equal to the sum of the counterclockwise torques

  • This is known as the principle of torques (also called the principle of moments)

  • It can be applied to a range of scenarios, such as the balanced beam or seesaw problem

    • These problems usually involve objects on opposite sides of a lever (such as a seesaw) balancing one another

  • This type of problem can be solved by

    • identifying the location of the pivot and calculating the torque due to each force about this point

    • summing the clockwise torques and counterclockwise torques separately

    • using the principle of torques to calculate the unknown quantity

A beam in rotational equilibrium

Physics diagram of a lever with forces F1, F2, and F3 acting on it at distances r1, r2, and r3 respectively from the pivot, illustrating the moment formula.
When the forces on a beam are balanced on each side of a pivot, the net torque on the beam is zero, so it will be in rotational equilibrium

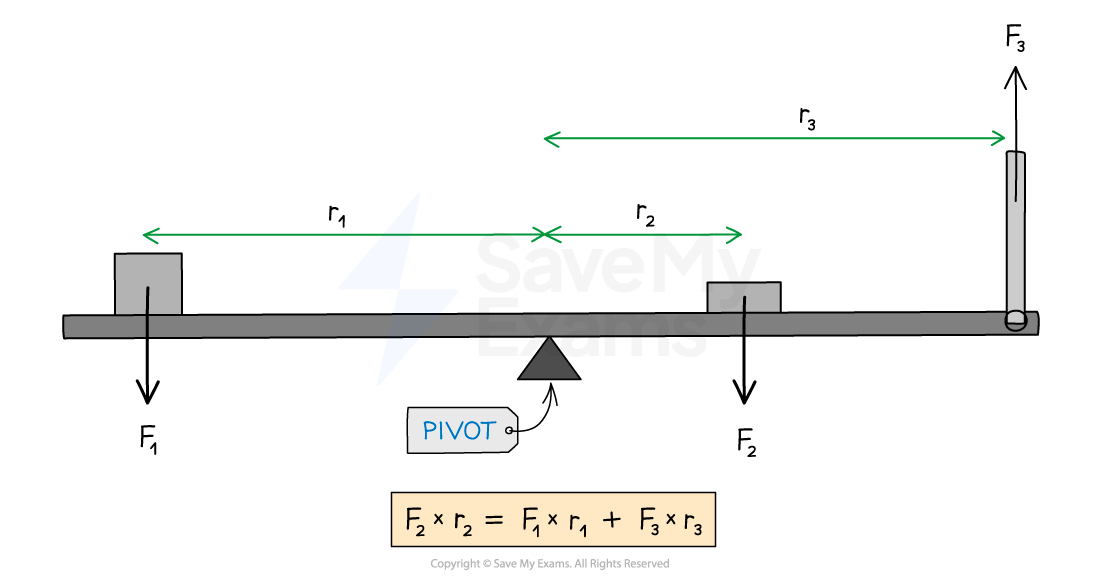
Worked Example

Four beams of the same length each have three forces acting on them and pivot about their center of mass.

Which of the following beams is in rotational equilibrium?

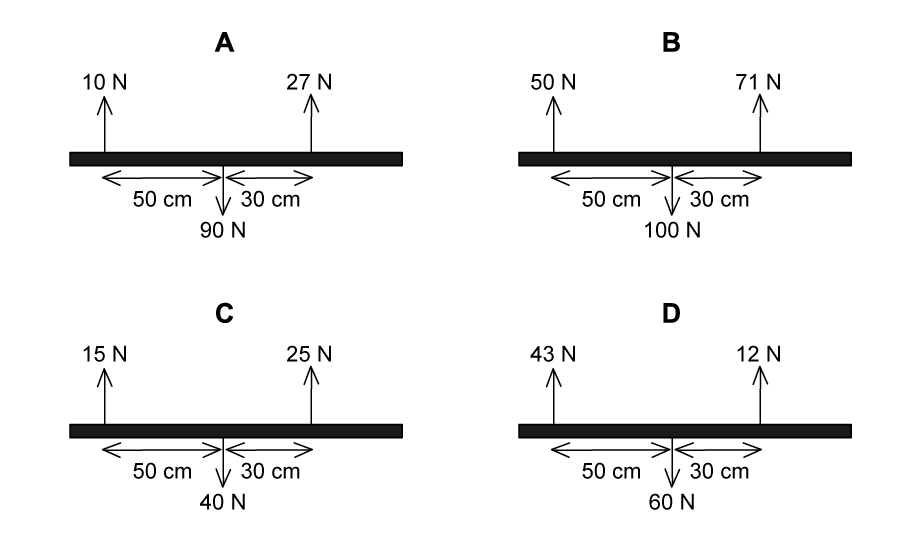
Four diagrams labeled A to D showing forces on beams. Forces and distances vary: A (10N, 27N, 90N), B (50N, 71N, 100N), C (15N, 25N, 40N), D (43N, 12N, 60N).

The correct answer is C

Answer:

Step 1: Analyze the scenario

  • A beam is in rotational equilibrium when there is a net torque of zero acting on it, and this means that:

Total clockwise torque = total counterclockwise torque

  • Each force acts perpendicular to the beam, so each torque is equal to

tau space equals space F r space sin space 90 degree space equals space F r

  • Since the weight of each beam acts at the center of mass (i.e. r space equals space 0), this force does not produce a torque

Step 2: Determine the net torque on each beam

  • Beam A

    • Total clockwise torque = 10 × 50 = 500 N cm

    • Total counterclockwise torque = 27 × 30 = 810 N cm

    • Beam A has a net counterclockwise torque of 310 N cm

  • Beam B

    • Total clockwise torque = 50 × 50 = 2500 N cm

    • Total counterclockwise torque = 71 × 30 = 2130 N cm

    • Beam B has a net clockwise torque of 370 N cm

  • Beam C

    • Total clockwise torque = 15 × 50 = 750 N cm

    • Total counterclockwise torque = 25 × 30 = 750 N cm

    • Beam C has a net torque of 0

  • Beam D

    • Total clockwise torque = 43 × 50 = 2150 N cm

    • Total counterclockwise torque = 12 × 30 = 360 N cm

    • Beam D has a net clockwise torque of 1790 N cm

Step 3: Identify the correct answer

  • Only beam C has a net torque of zero, so it is in rotational equilibrium

Worked Example

A uniform plank of mass 30 kg and length 10 m is supported at its left end and at a point 1.5 m from its center of mass.

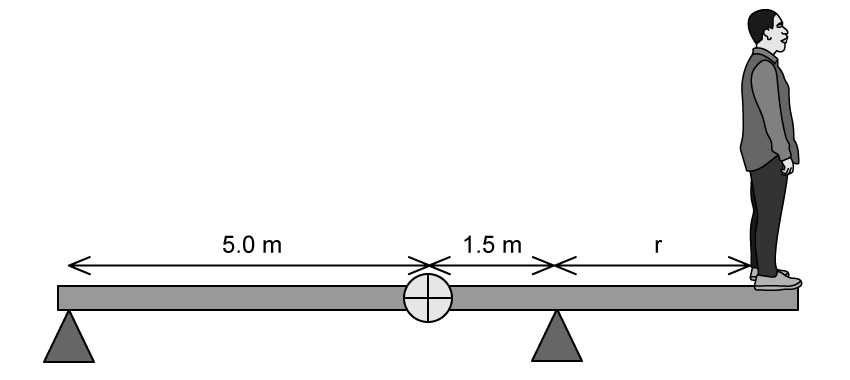
Diagram of a person standing on the right end of a balanced beam with support points at 5.0 meters and 1.5 meters from the center, labeled distances shown.

Calculate the maximum distance r a child of mass 50 kg can walk before the plank begins to tip over.

Answer:

Step 1: Analyze the scenario

  • Normal forces, F subscript L and F subscript R, act vertically upwards at each support

  • Before the plank begins to tip, the system is in rotational equilibrium, so sum tau subscript n e t end subscript space equals space 0

  • Once the plank starts moving, the normal force from the left support force F subscript L becomes zero as the rod and support are no longer in contact

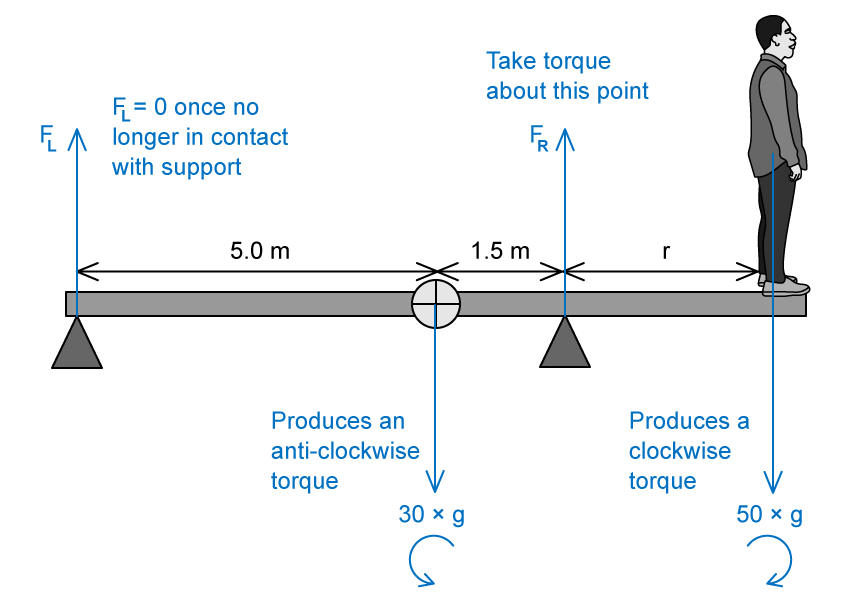
Diagram showing a beam balanced on two supports with forces and torques labeled. A person stands on the right end. The left part shows 5m, right part 1.5m.

Step 2: Determine the torques about the axis of rotation

  • Each force acts perpendicular to the beam, so each torque is equal to

tau space equals space F r space sin space 90 degree space equals space F r

  • When the plank tips, the right support will act as the axis of rotation

  • Taking torques about the right support:

    • The torque due to F subscript R is zero

    • Total clockwise torque = 50 g cross times r space equals space 50 g r

    • Total counterclockwise torque = 30 g cross times 1.5 space equals space 45 g

Step 3: Equate the clockwise and anti-clockwise torques

  • When the plank is in rotational equilibrium:

Total clockwise torque = total counterclockwise torque

50 g r space equals space 45 g

50 up diagonal strike g r space equals space 45 up diagonal strike g

r space equals space 45 over 50 space equals space 0.9 space straight m

  • Therefore, the plank will begin to tip when the child is 0.9 m from the right support

Examiner Tips and Tricks

When considering a system in rotational equilibrium, choosing certain points can simplify calculations of net torque. You can choose any point as long as you can relate it to the system's axis of rotation.

To simplify your calculation, choose a point where most forces are acting, as the torque due to these points becomes zero. When you need to determine the point where the net torque is zero, choose a point through which the lines of action of the forces pass.

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Parallel Axis TheoremNext:Newton’s First Law in Rotational Form
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.