Newton’s Second Law in Rotational Form (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Katie M

Expertise

Physics

Newton’s second law in rotational form

The rotational analog of Newton's second law states:

The rate of change of angular velocity, or angular acceleration, of a rigid system is directly proportional to the net torque exerted on the rigid system and is in the same direction

It is defined by the equation:

$α_{s y s} = \frac{\sum τ}{I_{s y s}} = \frac{τ_{n e t}}{I_{s y s}}$

Where:
- $α_{s y s}$ = angular acceleration of the system, measured in $rad / s^{2}$
- $τ_{n e t}$ = net torque exerted on the system, measured in $N \cdot m$
- $I_{s y s}$ = rotational inertia of the system, measured in $kg \cdot m^{2}$
Newton's second law states that angular acceleration is:
- directly proportional to the net torque exerted on the rigid system
- inversely proportional to the rotational inertia of the rigid system
Therefore, the angular velocity of a rigid system will
- change if the net torque exerted on that system is not equal to zero
- remains constant if the net torque exerted on that system is equal to zero

Solving problems involving linear and rotational motion

A rigid system may have multiple forces and torques acting on it, for example
- a beam suspended by a rope
- pulley-mass systems
Torques and linear forces act independently
- Therefore, to fully describe such a system, calculations involving linear and rotational quantities may need to be performed independently
These types of questions usually involve the following concepts and equations
- Net force is zero for systems in translational equilibrium: $\sum_{i} \vec{F_{i}} = 0$
- Net torque is zero for systems in rotational equilibrium: $\sum τ_{i} = 0$
- Unbalanced forces produce linear acceleration: $F_{n e t} = m a$
- Unbalanced torques produce angular acceleration: $τ_{n e t} = I α$
- The relationship between tangential and angular velocity: $v_{T} = r ω$
- The relationship between tangential and angular acceleration: $a_{T} = r α$

Comparison of linear and rotational variables in Newton's second law

linear variable	rotational variable
force $F$	torque $τ$
mass $m$	rotational inertia $I$
acceleration $a$	angular acceleration $α$
Newton's second law $F \propto a$	Newton's second law $τ \propto α$
$F_{n e t} = m a$	$τ_{n e t} = I α$

Worked Example

A block of mass $m$ is attached to a string that is wrapped around a cylindrical pulley of mass $M$ and radius $R$ , as shown in the diagram.

The rotational inertia of the cylindrical pulley about its axis is $\frac{1}{2} M R^{2}$

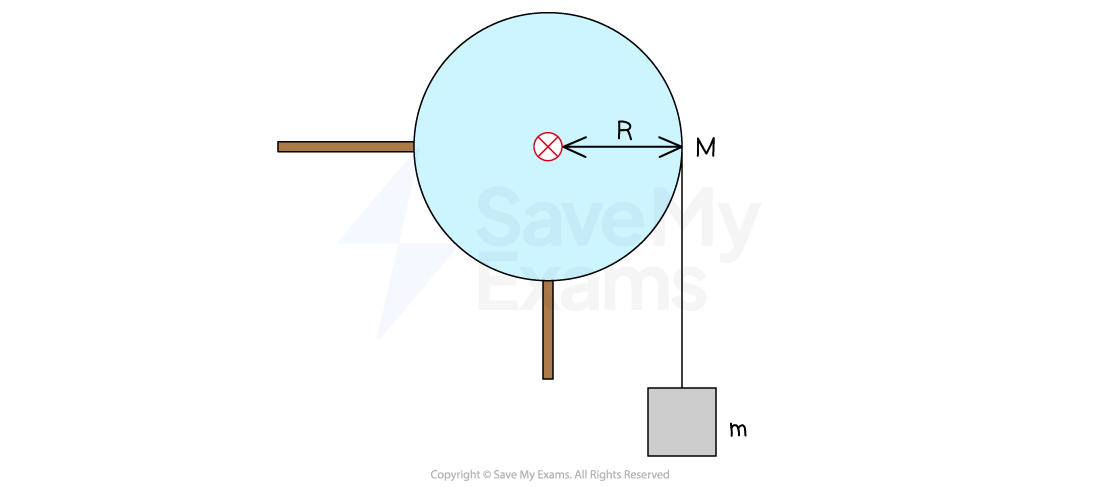
Diagram showing a cylindrical pulley of mass M and radius R, with a mass m hanging from its edge.

When the block is released, the pulley begins to turn as the block falls.

Derive an expression for the acceleration of the block in terms of $m$ , $M$ and $g$ .

Answer:

Step 1: Analyze the scenario

There is linear motion due to the forces exerted on the block from:
- the weight of the block
- the tension in the string
There is rotational motion due to the torque exerted on the pulley from the tension in the string at the radius

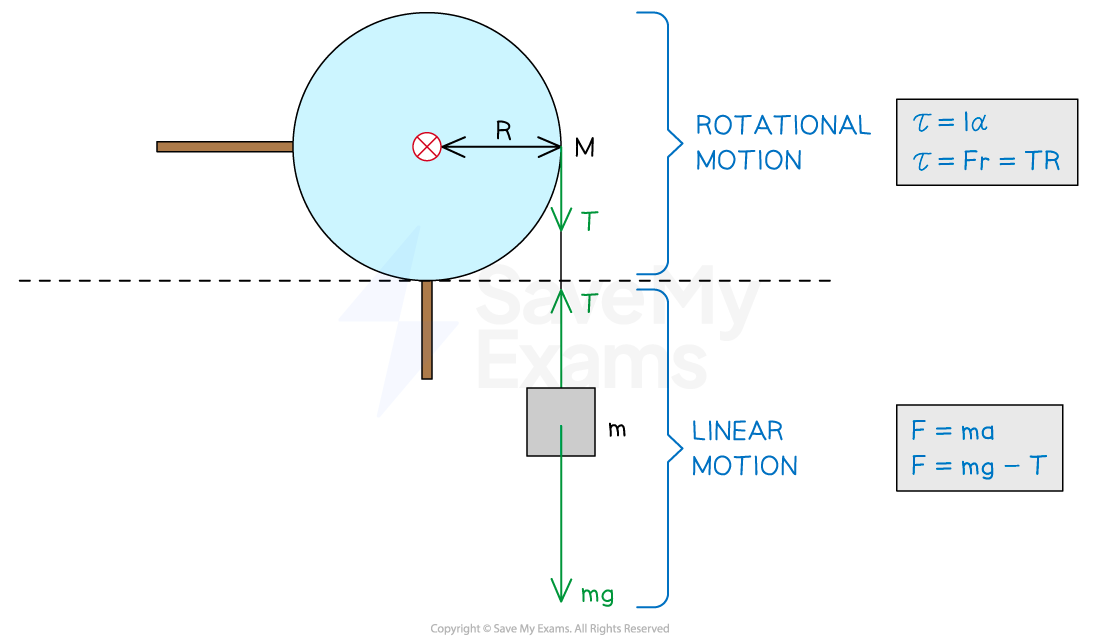
Diagram showing rotational motion with a cylindrical pulley of radius R and mass M, and linear motion with a mass m hanging from a string. Equations for both motions provided.

Step 2: Apply Newton's second law to the motion of the block

A net force produces a linear acceleration

$F_{n e t} = m a$

$m g - T = m a$ eq. (1)

Step 3: Apply Newton's second law to the rotation of the pulley

A net torque produces angular acceleration
- For radius $R$

$τ = I α$

$T R = I α$

Step 4: Write the expression in terms of linear acceleration

The relationship between angular acceleration and tangential acceleration of the pulley is:

$α = \frac{a}{R}$

Substitute this into the previous equation:

$T R = I \frac{a}{R}$

Step 5: Substitute the rotational inertia into the expression

The rotational inertia of the cylinder is $I = \frac{1}{2} M R^{2}$

$T R = (\frac{1}{2} M R^{2}) \frac{a}{R}$

$T = (\frac{1}{2} M R^{2}) \frac{a}{R^{2}}$

$T = \frac{1}{2} M a$ eq. (2)

Step 6: Write the final expression for linear acceleration

Substitute eq. (2) into eq. (1)

$m g - (\frac{1}{2} M a) = m a$

$m g = m a + \frac{1}{2} M a$

$m g = a (m + \frac{1}{2} M)$

$a = \frac{m g}{m + \frac{1}{2} M}$

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?