Frequency & Period of SHM (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Written by: Dan Mitchell-Garnett

Reviewed by: Caroline Carroll

Frequency & period

Relationship between frequency and period

A cycle of a system in SHM is when the system performs a complete oscillation and returns to its initial position

One complete cycle of a pendulum

Diagram showing a pendulum's motion in one oscillation, marked at five positions with arrows indicating the direction of movement. Caption reads: "1 Oscillation (T)". — **A cycle is complete when the system returns to the initial state. In this case, the initial state is the mass in the equilibrium position while moving left**

The period of a system in SHM is the time taken for one complete cycle to occur
The frequency of a system is the number of cycles which are completed in one second
The period and frequency are related by the following equation:

$T = \frac{1}{f}$

Where:
- $T$ = period of an oscillation, measured in $s$
- $f$ = frequency of the oscillations, measured in $Hz$

Effect of amplitude on period

Amplitude is defined as:

the maximum displacement of the object in SHM from its equilibrium position

One characteristic feature of SHM is that amplitude does not affect period
Increasing or decreasing the amplitude of a swinging pendulum or mass-spring system, for example, will not alter the period or frequency of that system

Period of an ideal spring

An object-ideal spring oscillator can be a horizontal or vertical oscillating system in which an object with mass is attached to an ideal spring

Object-ideal spring systems

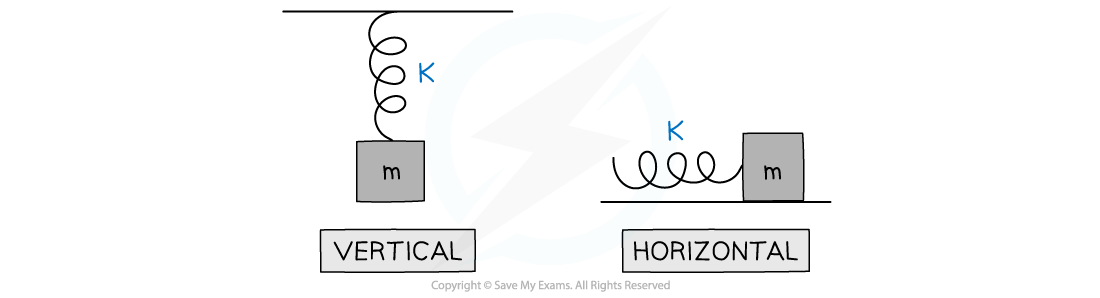
Diagram showing a mass (m) attached to a spring (k) in two configurations: vertical on the left and horizontal on the right, with labels "VERTICAL" and "HORIZONTAL". — **An object-ideal spring system can oscillate vertically or horizontally**

The period of an object-ideal spring system is given by:

$T_{s} = 2 π \sqrt{\frac{m}{k}}$

Where:
- $T_{s}$ = period of the ideal spring, measured in $s$
- $m$ = mass of the object, measured in $kg$
- $k$ = spring constant of the ideal spring, measured in $N / m$
This equation applies to both vertical and horizontal object-ideal spring systems

Worked Example

Diagram of a mass m connected to two springs in series with constants kx and ky on a horizontal surface.

The horizontal object-ideal spring system above has two springs attached in series to an object with mass $m$ . The springs have spring constants $k_{x}$ and $k_{y}$ .

An effective spring constant is the spring constant of a single spring that would behave the same as the two springs combined.

You may assume that each spring experiences the same force.

Derive an expression for the period of the system in terms of $m$ , $k_{x}$ and $k_{y}$ by finding the system's effective spring constant.

Answer:

Step 1: Analyze the scenario

This system is very similar to a standard horizontal object-ideal spring system, however there are now two springs instead of one.

To answer the question, find an expression for the effective spring constant. The question states that force is evenly distributed between the springs. This means the same value for force can be used for both springs.

Writing the object's displacement in terms of the spring constants will be

Step 2: Find the effective spring constant of this system

When the object is at a displacement $Δ x$ from the equilibrium position, this displacement is the sum of the extension of each spring:

$Δ x = Δ x_{x} + Δ x_{y}$

Where:
- $Δ x_{x}$ is the extension of spring x, measured in $m$
- $Δ x_{y}$ is the extension of spring y, measured in $m$
The extensions can be written in terms of force and spring constants using Hooke's law:

$F_{x} = - k_{x} Δ x_{x}$

$Δ x_{x} = - \frac{F_{x}}{k_{x}}$

$Δ x_{y} = - \frac{F_{y}}{k_{y}}$

Recall that force is evenly distributed, so the forces exerted by each spring are equal:

$F_{x} = F_{y} = F$

$Δ x = Δ x_{x} + Δ x_{y} = (- \frac{F}{k_{x}}) + (- \frac{F}{k_{y}})$

Recall Hooke's law is:

$F = - k Δ x$

Write this equation in the format of Hooke's law for a single spring:

$Δ x = - (\frac{1}{k_{x}} + \frac{1}{k_{y}}) F$

$F = - (\frac{1}{\frac{1}{k_{x}} + \frac{1}{k_{y}}}) Δ x = - (\frac{k_{x} k_{y}}{k_{x} + k_{y}}) Δ x$

From this equation, it can be determined that the effective spring constant, $k_{e}$ , is:

$k_{e} = \frac{k_{x} k_{y}}{k_{x} + k_{y}}$

Step 3: Substitute this into the equation for the period of an object-ideal spring system

Find the equation for the period of this system from the equation sheet:

$T_{s} = 2 π \sqrt{\frac{m}{k}}$

Substitute $k_{e}$ in place of $k$ in this equation to produce the final equation:

$T_{s} = 2 π \sqrt{\frac{m}{\frac{k_{x} k_{y}}{k_{x} + k_{y}}}}$

This can be simplified to the following:

$T_{s} = 2 π \sqrt{\frac{m (k_{x} + k_{y})}{k_{x} k_{y}}}$

Examiner Tips and Tricks

This equation for this system's period appears on your equation sheet:

$T_{s} = 2 π \sqrt{\frac{m}{k}}$

You do not need to know the derivation. You may, however, need to rearrange it to find frequency or use it to derive new equations.

Additionally, this equation looks similar to the period for a pendulum, make sure you know which equation applies to which system. This equation features the spring constant, which may help to remind you.

Period of a simple pendulum

A pendulum consists of a mass suspended from a string which oscillates side to side
The period of an oscillating pendulum is given by:

$T_{p} = 2 π \sqrt{\frac{l}{g}}$

Where:
- $T_{p}$ = the period of one cycle of the pendulum, measured in $s$
- $l$ = length of the string, measured in $m$
- $g$ = acceleration due to gravity at Earth’s surface, measured in $m / s^{2}$
This equation applies to a pendulum which is displaced by a small angle only

Worked Example

Which equation correctly shows the frequency of a pendulum of length $l$ oscillating through a small angle?

A: $f_{p} = 2 π \sqrt{\frac{g}{l}}$

B: $f_{p} = \frac{1}{2 π} \sqrt{\frac{l}{g}}$

C: $f_{p} = \frac{1}{2 π} \sqrt{\frac{g}{l}}$

D: None of the above

Answer: C

Step 1: Analyze the scenario

A pendulum of length $l$ is oscillating through a small angle
This means it can be modeled as SHM

Step 2: Recall the relevant equations

From the equation sheet, the relevant equation for a pendulum's period is:

$T_{p} = 2 π \sqrt{\frac{l}{g}}$

Recall that frequency is the reciprocal of period:

$f = \frac{1}{T}$

Step 3: Apply the specific conditions

Substitute the period of a pendulum into this equation for frequency:

$f_{p} = \frac{1}{2 π \sqrt{\frac{l}{g}}}$

Simplify this expression:

$f_{p} = \frac{1}{2 π} \cdot \frac{1}{\sqrt{\frac{l}{g}}} = \frac{1}{2 π} \sqrt{\frac{g}{l}}$

Therefore the correct answer is C

Examiner Tips and Tricks

Again, this equation is given on the equation sheet and you will not be expected to derive it in your exam. You may, however, be required to demonstrate that the restoring torque in this system arises from a component of weight acting perpendicular to the string.

The weight force of the mass in a pendulum system acts downwards. A component of this acts perpendicular to the line of the string at the extreme end of the oscillation. This has the value m g sin θ.

Last updated: 29 August 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Defining Simple Harmonic MotionNext:Features of SHM

Frequency & Period of SHM (College Board AP® Physics 1: Algebra-Based)

Study Guide

Frequency & period

Relationship between frequency and period

One complete cycle of a pendulum

Effect of amplitude on period

Period of an ideal spring

Object-ideal spring systems

Worked Example

Examiner Tips and Tricks

Period of a simple pendulum

Worked Example

Examiner Tips and Tricks

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Dan Mitchell-Garnett

Author: Caroline Carroll