Defining Simple Harmonic Motion (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Dan Mitchell-Garnett

Expertise

Physics Content Creator

Defining simple harmonic motion

What is simple harmonic motion?

Simple harmonic motion (SHM) is a special case of periodic motion
In SHM, an object oscillates regularly around an equilibrium position:

An equilibrium position is a location at which the net force exerted on an object is zero

This is where displacement $x$ is defined as zero so the equilibrium position will often be labeled with $x = 0$

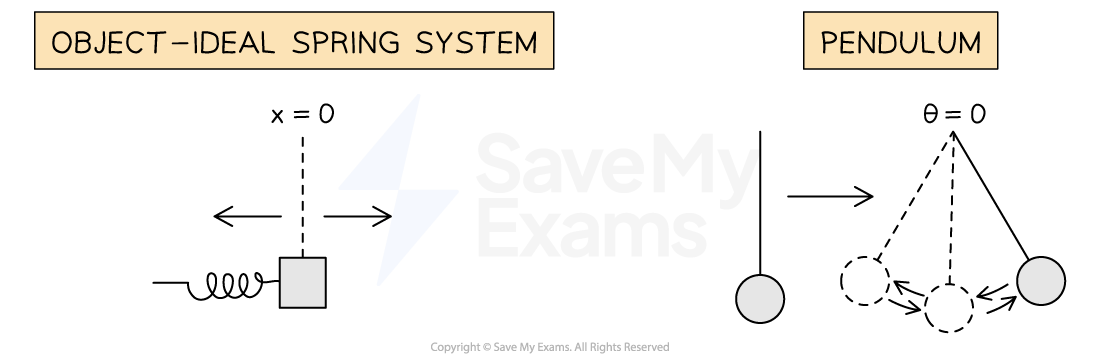
Examples of systems that exhibit SHM:
- An object attached to a spring oscillating horizontally across a frictionless surface (often called an object-ideal spring system)
- A pendulum (object suspended from a string) with a small angular displacement

Systems in simple harmonic motion

Two diagrams illustrate a mass spring system and a pendulum. The mass spring system shows a mass moving horizontally. The pendulum diagram shows a bob swinging. — **Different systems can undergo SHM. A pendulum and object-ideal spring system are just two examples.**

Conditions for simple harmonic motion

A restoring force is required for SHM:

A restoring force always acts in a direction opposite to the object’s displacement from an equilibrium position

The condition for SHM is that the restoring force is proportional to the displacement of the object from the equilibrium position but in the opposite direction

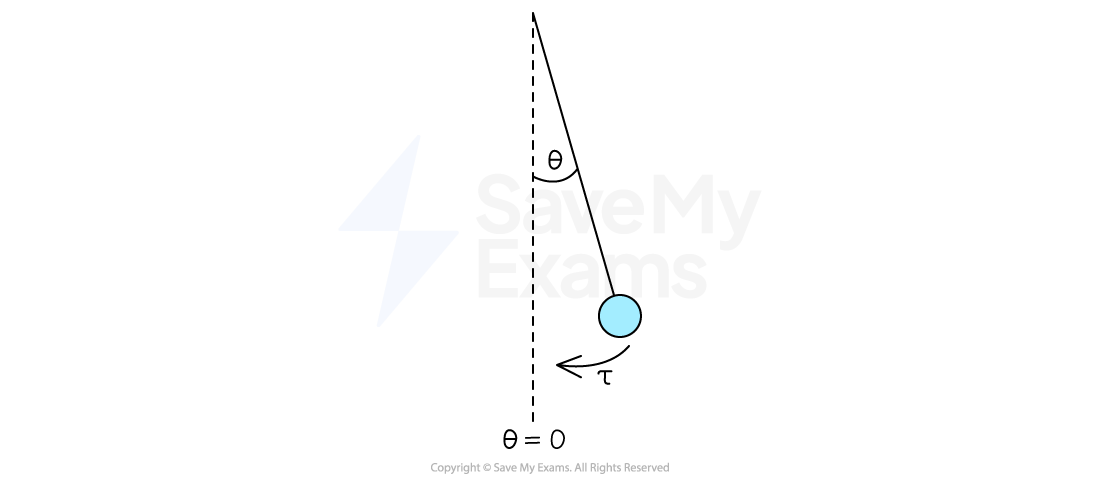
Conditions for a pendulum in SHM

A linear system, such as an object-ideal spring system, requires a restoring force in the opposite direction to linear displacement
A pendulum, however, is better described as moving through angular displacement
This means that, for a pendulum to undergo SHM, a restoring torque must be proportional to angular displacement but act in the opposite direction
- These quantities are only proportional for small angular displacements
- A pendulum can only be modeled as SHM when the angle is small

SHM in a pendulum

A pendulum with the angle to the vertical labelled as θ and the torque acting towards the equilibrium position marked as τ. — **Angular displacement and torque are proportional for a pendulum, provided that angular displacement is small.**

Derived equation

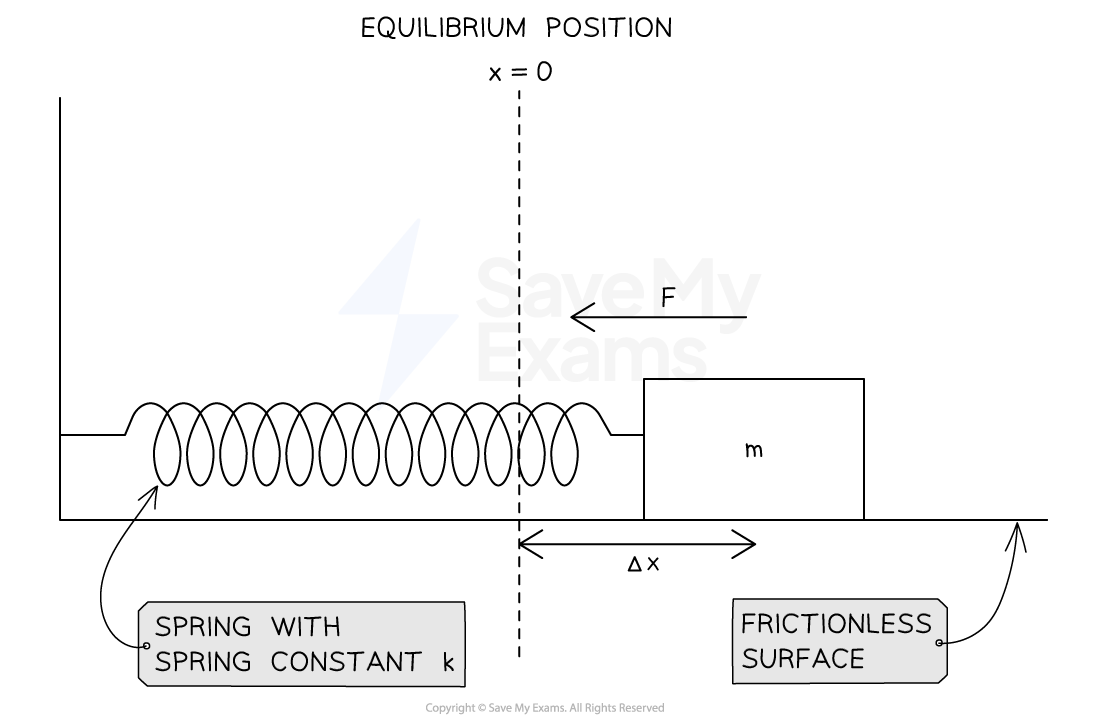
Simple harmonic motion of an object-ideal spring system can be characterized by the equation:

$m a_{x} = - k Δ x$

This shows that the acceleration of the object is proportional to the displacement and acts in the opposite direction

Object-ideal spring system

A horizontal spring is connected to an object of mass m. The object is at a displacement Δx from equilibrium, with a restoring force F acting back towards equilbrium. — **The restoring force acts in the opposite direction to displacement and always towards the equilibrium position. In this system, the restoring force comes from the spring.**

Derivation

Step 1: Identify the fundamental equations

Recall Hooke's law:

$\vec{F_{s}} = - k Δ \vec{x}$

Where:
- ${\vec{F}}_{s}$ = spring's force measured in $N$
- $k$ = spring constant of the spring, measured in $N / m$
- $Δ \vec{x}$ = displacement of the object from the equilibrium position, measured in $m$
This describes the restoring force, as it acts in the opposite direction to the displacement vector
Recall Newton's second law, which relates the force on an object with its mass and acceleration:

${\vec{F}}_{n e t} = m \vec{a}$

Where:
- ${\vec{F}}_{n e t}$ = net force on the mass, measured in $N$
- $m$ = the object's mass, measured in $kg$
- $\vec{a}$ = the object's acceleration, measured in $m / s^{2}$

Step 2: Apply the specific conditions

The spring's restoring force is the only force that acts, therefore:

$F_{n e t} = F_{s}$

Additionally, all forces act in the x direction so Hooke's law and Newton's second law can be rewritten as:

$F_{s} = - k Δ x$

$F_{n e t} = m a_{x}$

Where:
- $a_{x}$ is the acceleration in the x direction, measured in $m / s^{2}$
Substituting Hooke's law and Newton's second law into the above gives:

$m a_{x} = - k Δ x$

This is the derived equation and does not appear on the equation sheet

Examiner Tip

The derived equation applies specifically to the system described. To derive a similar equation for a different system you must identify the restoring force, apply the conditions for simple harmonic motion and combine these with Newton's second law.

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?