AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 7: OscillationsRepresenting and Analyzing SHMFeatures of SHM

Features of SHM (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself
Dan Mitchell-Garnett

Written by: Dan Mitchell-Garnett

Reviewed by: Caroline Carroll

Features of SHM

Displacement, velocity and acceleration

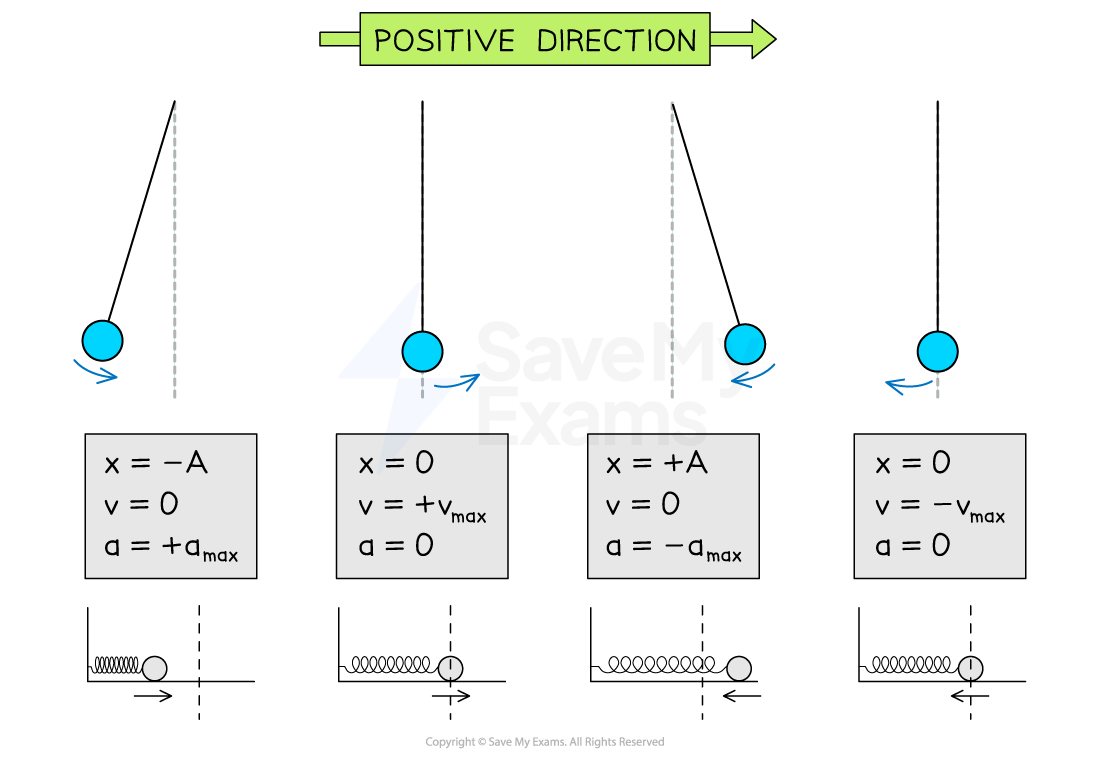
  • The amplitude positions of an oscillating system refer to the furthest points from equilibrium on either side

    • One side of the equilibrium should be chosen as the positive and the other as the negative

    • Usually, the left side (or lower side) is negative and the right side (or upper side) positive

  • As the system in SHM oscillates between amplitude positions, the values of displacement, velocity and acceleration are constantly varying

    • Each quantity alternates between a (positive) maximum value and a (negative) minimum value throughout a cycle

    • This means each quantity is zero at some point in the cycle

  • These minima, maxima and zeroes are characteristic features of SHM

Displacement

  • At the negative amplitude position:

    • Displacement has a minimum value of negative A

    • Here, A is amplitude, the greatest distance from equilibrium position

  • At the positive amplitude position:

    • Displacement has a maximum value of plus A

  • At the equilibrium position:

    • Displacement has a value of 0

Velocity

  • At the negative amplitude position:

    • Velocity has a value of 0

    • The object is temporarily stationary as it changes direction

  • At the positive amplitude position:

    • Velocity has a value of 0

  • At the equilibrium position:

    • Velocity has a maximum value of plus v subscript m a x end subscriptif the object is travelling in the positive direction

    • Velocity has a minimum value ofnegative v subscript m a x end subscript if the object is travelling in the negative direction

Acceleration

  • At the negative amplitude position:

    • Acceleration has a maximum value of plus a subscript m a x end subscript

    • Acceleration acts in the opposite direction to displacement, which is a defining feature of SHM

  • At the positive amplitude position:

    • Acceleration has a maximum value of negative a subscript m a x end subscript

  • At the equilibrium position:

    • Acceleration has a value of 0

    • The restoring force has a value of 0 here

Changing quantities in SHM

The far left, equilibrium and far right positions of an object-ideal spring oscillator and a pendulum are shown and lined up on top of each other. At each position, the values of acceleration, displacement and velocity are shown. These values are stated in the text above this image.
At the extremes, velocity is zero and displacement and acceleration have maxima or minima. The opposite is true for the equilibrium position. This applies to a pendulum or an object-ideal spring system.

Examiner Tips and Tricks

Acceleration has the greatest magnitude at the extremes because this is where the restoring force is strongest. Force and acceleration are directly proportional, following Newton's second law.

Calculating displacement in SHM

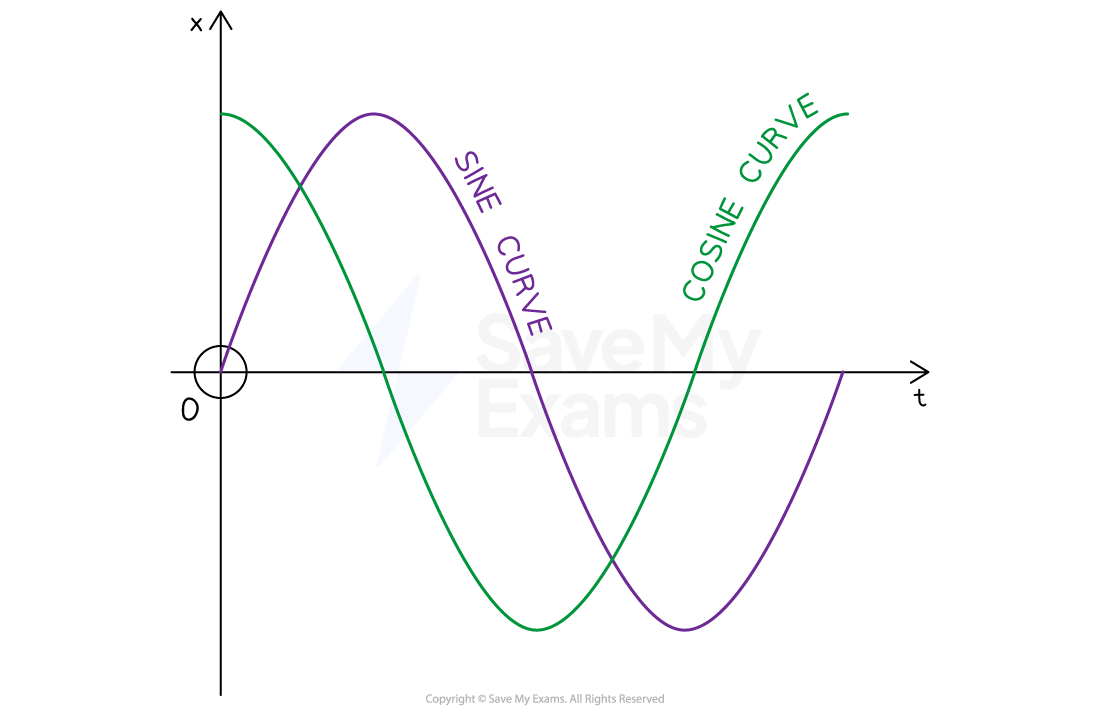
Sine and cosine

  • Displacement in SHM alternates smoothly between maxima and minima over time with a constant frequency

  • Sinusoidal graphs (sine or cosine) also alternate smoothly between maxima and minima with a constant frequency

  • In SHM, the variation of displacement with time can therefore be represented graphically using a sine or a cosine graph

    • A sine graph begins with its y axis at 0, whereas a cosine graph begins with its y axis at the maximum value

    • Either graph can represent displacement against time, it depends on when t space equals space 0 is defined

Sine graph and cosine graph

A sine curve begins at the origin, curves up to a maximum, passes back through zero, reaches a minimum and curves back up to zero in a single cycle. A cosine curve starts at a maximum, decreases to zero and continues to decrease until it reaches a minimum. This minimum occurs at the same time as the sine graph passing back through zero. The cosine curve then moves back up through zero and reaches a maximum again at the end of a single cycle.
A sine curve begins with a displacement of zero at a time of zero, whereas a cosine curve begins with the oscillator at maximum amplitude at a time of zero.

Displacement equations

  • To calculate the displacement from equilibrium for an object oscillating in SHM, one of the following equations can be used:

x space equals space A cos open parentheses 2 straight pi f t close parentheses

x space equals space A sin open parentheses 2 straight pi f t close parentheses

  • Where:

    • xis the object's displacement from equilibrium position, measured in straight m

    • A is the amplitude of the oscillation, measured in straight m

    • f is the frequency of oscillations, measured in Hz

    • t is the time at which displacement is being calculated, measured in straight s

  • The cosine equation is used if t space equals space 0 space straight s is defined when the object's displacement is at a maximum

  • The sine equation is used if t space equals space 0 space straight s is defined when the object's displacement is zero

Examiner Tips and Tricks

Pay close attention to the wording of questions where you need to use these equations. You are unlikely to find a sentence telling you 'at a time of zero the displacement is also zero'.

Statements like 'the mass is pulled 5 cm from equilibrium and then released' or 'the ball is in equilibrium. Oscillations begin when it is struck'. The first sentence tells you to use cosine as oscillations start from the amplitude position, while the second sentence tells you to use sine as oscillations begin from equilibrium.

Additionally, ensure your calculator is in radians mode for this equation, not degrees.

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Frequency & Period of SHMNext:Graphical Representation of SHM
    Author
    Reviewer
    Dan Mitchell-Garnett

    Author: Dan Mitchell-Garnett

    Expertise: Physics Content Creator

    Dan graduated with a First-class Masters degree in Physics at Durham University, specialising in cell membrane biophysics. After being awarded an Institute of Physics Teacher Training Scholarship, Dan taught physics in secondary schools in the North of England before moving to Save My Exams. Here, he carries on his passion for writing challenging physics questions and helping young people learn to love physics.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.