Kinetic Energy & Potential Energy of SHM (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Dan Mitchell-Garnett

Expertise

Physics Content Creator

Kinetic energy & potential energy of SHM

Energy changes in SHM

Graph of potential and kinetic energies

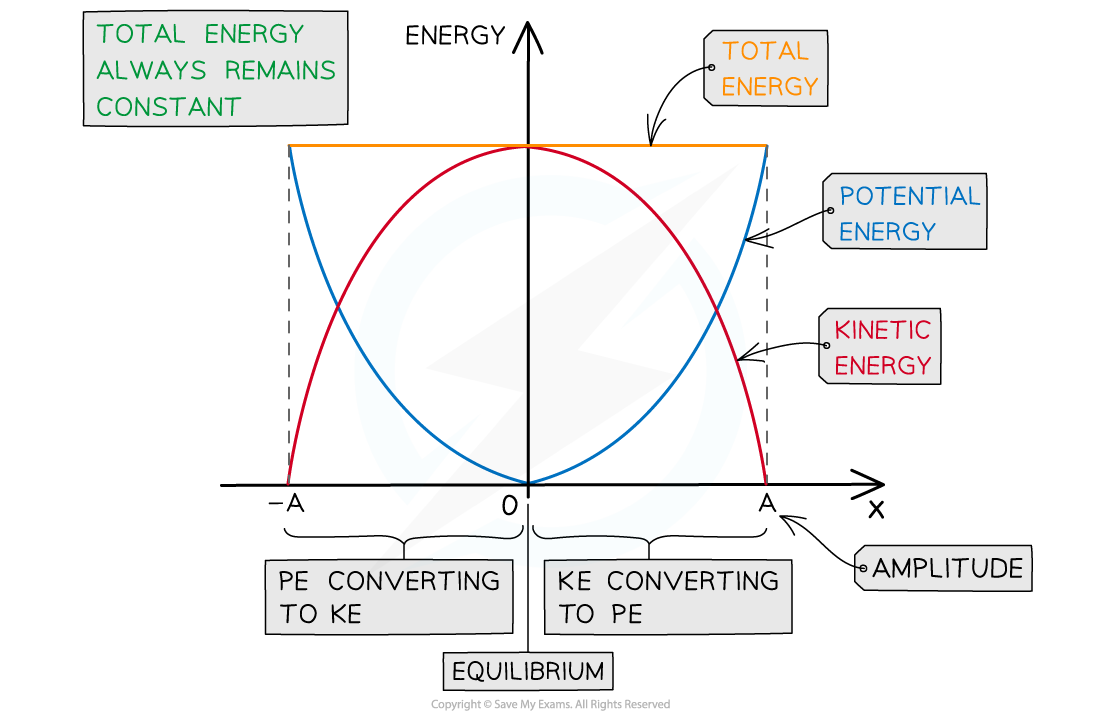
Graph showing energy changes with axes labeled 'Energy' and 'x'. Total energy is constant. Potential energy decreases to zero then increases while kinetic energy increases from zero then decreases between positions -A and A. — **The sum of kinetic and potential energy is always the same value in an ideal system in SHM.**

Kinetic energy and potential energy vary throughout a cycle for a system displaying SHM
However, unlike displacement, velocity and acceleration, kinetic and potential energies only vary from zero to a maximum
- Energy is a scalar quantity and cannot have negative values
Where potential energy is at a maximum, kinetic energy is zero
Where kinetic energy is at a maximum, potential energy is zero

Variation in kinetic energy

Recall that kinetic energy is proportional to velocity squared
At the amplitude positions:
- Velocity is zero as the object changes direction
- At these points, kinetic energy is zero
- Kinetic energy cannot have a value lower than zero
At the equilibrium position travelling in the positive direction:
- Velocity has a maximum positive value
- Kinetic energy has a maximum positive value
At the equilibrium position travelling in the negative direction:
- Velocity has a minimum negative value
- Kinetic energy still has a maximum positive value, as squaring the velocity negates its negative sign

Variation in potential energy

Work done by the restoring force in the opposite direction to displacement goes into the potential store
- When the magnitudes of the restoring force and displacement are greatest, the potential energy has a maximum value
At the equilibrium position:
- Displacement from equilibrium is zero
- No work is done against the restoring force
- Potential energy of the system is zero
At the amplitude positions:
- The magnitudes of displacement and the restoring force are both maximum
- Potential energy has a maximum value

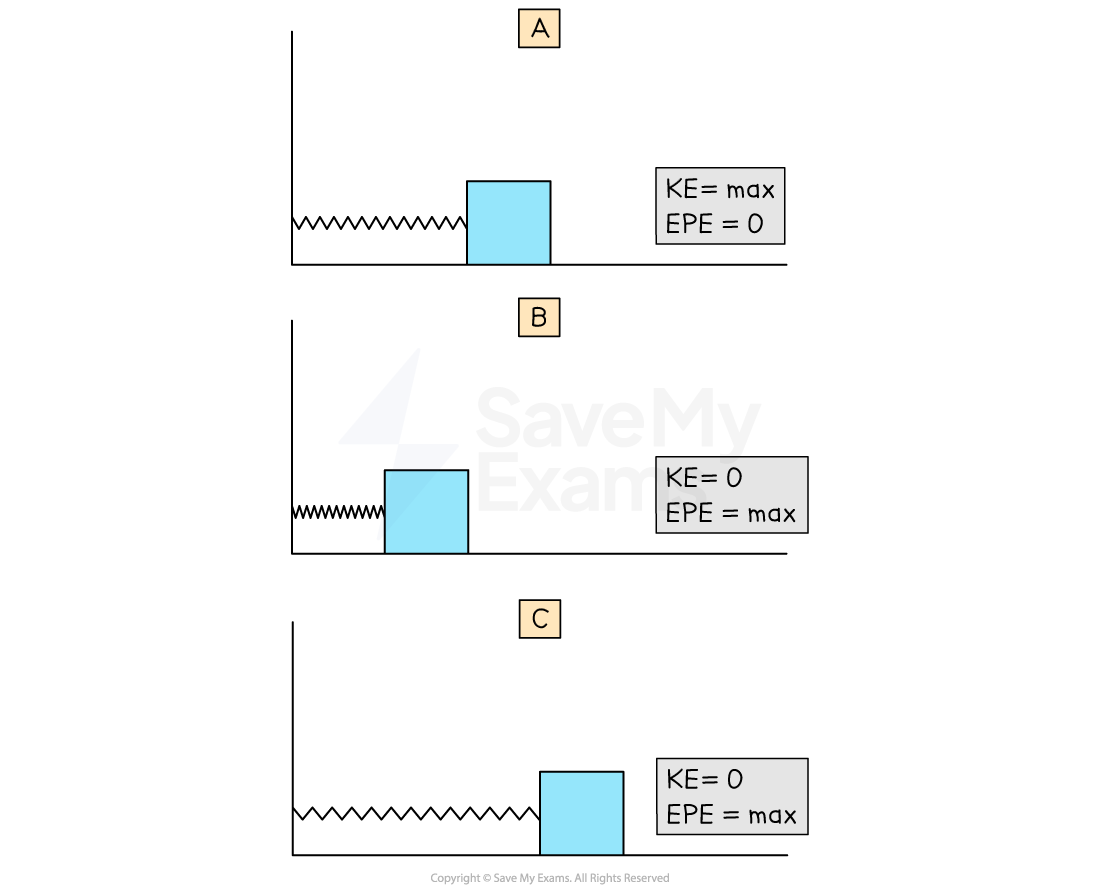
Potential and kinetic energies at different positions

Three diagrams labeled A, B, and C showing an object on a horizontal surface with a spring. A: spring is at equilibrium, KE = max, EPE = 0. B: spring is compressed KE = 0, EPE = max. C: spring is extended KE = 0, EPE = max. — **A shows the system's equilibrium position. Here, kinetic energy is maximum. B and C show the amplitude positions. Here, potential energy is maximum.**

Total energy

The total energy in SHM remains constant
At every value of displacement, the sum of potential and kinetic energies is constant
- This means when potential energy is zero (at equilibrium), maximum kinetic energy is equal to the total energy
- Similarly, when kinetic energy is zero (at amplitude),maximum potential energy is equal to the total energy

Amplitude and total energy

Increasing the amplitude of oscillations increases the total energy in the system
The potential store of the SHM system is filled when the object moves against the restoring force, doing work
- If the amplitude of oscillations is increased, more work is done so the maximum potential energy also increases
If maximum potential energy increases, the total energy of the system increases

Total energy of an object-ideal spring system

Recall that the elastic potential energy stored in a spring is:

$U_{s} = \frac{1}{2} k {(Δ x)}^{2}$

Where:
- $U_{s}$ = elastic potential energy stored in the spring, measured in $J$
- $k$ = spring constant measured in $N / m$
- $Δ x$ = displacement, measured in $m$
When displacement is equal to amplitude, $A$ , potential energy is at a maximum:

$U_{m a x} = \frac{1}{2} k A^{2}$

Maximum potential energy is equal to total energy of the system:

$E_{t o t} = \frac{1}{2} k A^{2}$

Worked Example

A vertical spring with a spring constant of 80 N/m is suspended from a pole. A 0.4 kg block is connected to its lower end.

If the block is pulled 0.3 m from its equilibrium position and is released, what is its maximum speed?

Answer:

Step 1: Analyze the system

This is an object-ideal spring system displaying simple harmonic motion
The block is displaced 0.3 m from its equilibrium position, this is the amplitude of oscillations

Step 2: Apply the specific conditions

The total energy of the system is the sum of kinetic and potential energies

$E_{t o t a l} = U + K$

The potential energy of this system is in the form of elastic potential energy

$U = \frac{1}{2} k {(Δ x)}^{2}$

At the amplitude positions, kinetic energy is zero
- When kinetic energy is zero, potential energy is at a maximum

$E_{t o t a l} = U_{m a x} + 0$

At equilibrium, potential energy is zero
- When potential energy is zero, kinetic energy is at a maximum

$E_{t o t a l} = 0 + K_{m a x}$

Step 3: Consider the amplitude positions

At the amplitude positions, potential energy is equal to total energy
- Displacement is equal to amplitude, $A$

$E_{t o t a l} = \frac{1}{2} k A^{2}$

Step 4: Substitute the known quantities

Spring constant is 80 N/m
Amplitude is 0.3 m
Total energy is therefore:

$E_{t o t a l} = \frac{1}{2} \times 80 \times 0 . 3^{2}$

$E_{t o t a l} = 3.6 J$

Step 5: Consider the equilibrium position

At equilibrium, kinetic energy is equal to total energy
- Velocity is at a maximum here:

$E_{t o t a l} = \frac{1}{2} m {v_{m a x}}^{2}$

Step 6: Rearrange for maximum velocity and substitute known quantities

Rearrange for $v_{m a x}$ :

$v_{m a x} = \sqrt{\frac{2 E_{t o t a l}}{m}}$

Mass is 0.4 kg
Total energy is 3.6 J
Substitute these values into the rearranged equation:

$v_{m a x} = \sqrt{\frac{2 \times 3.6}{0.4}} = 4.2 m / s$

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?