Rate of Change of Momentum (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Written by: Katie M

Reviewed by: Caroline Carroll

Rate of change of momentum

Newton's second law of motion was originally postulated in terms of momentum
In terms of momentum, Newton's second law states

The rate of change of momentum is equal to the net external force exerted on an object (or system)

This can be written as:

${\vec{F}}_{n e t} = \frac{∆ \vec{p}}{∆ t}$

Where:
- ${\vec{F}}_{n e t}$ = net external force, measured in $N$
- $∆ \vec{p}$ = change in momentum, measured in $kg \cdot m / s$
- $∆ t$ = time interval, measured in $s$
The change in momentum is the difference between a system’s final momentum and its initial momentum, as written below:

change in momentum = final momentum − initial momentum

$∆ \vec{p} = \vec{p} - {\vec{p}}_{0}$

The equation above can be used in situations where the mass of the body is not constant
When the mass is constant:

${\vec{F}}_{n e t} = \frac{∆ \vec{p}}{∆ t} = \frac{\vec{p} - {\vec{p}}_{0}}{∆ t} = \frac{m \vec{v} - m {\vec{v}}_{0}}{∆ t} = \frac{m (\vec{v} - {\vec{v}}_{0})}{∆ t} = \frac{m ∆ \vec{v}}{∆ t}$

Since acceleration $\vec{a}$ is equal to the rate of change of velocity, the equation becomes:

${\vec{F}}_{n e t} = m \vec{a}$

Where:
- $m$ = mass of the body, measured in $kg$
- $∆ \vec{v}$ = change in velocity, measured in $m / s$
- $\vec{v}$ = final velocity, measured in $m / s$
- ${\vec{v}}_{0}$ = initial velocity, measured in $m / s$
- $\vec{a}$ = acceleration, measured in $m / s^{2}$

Worked Example

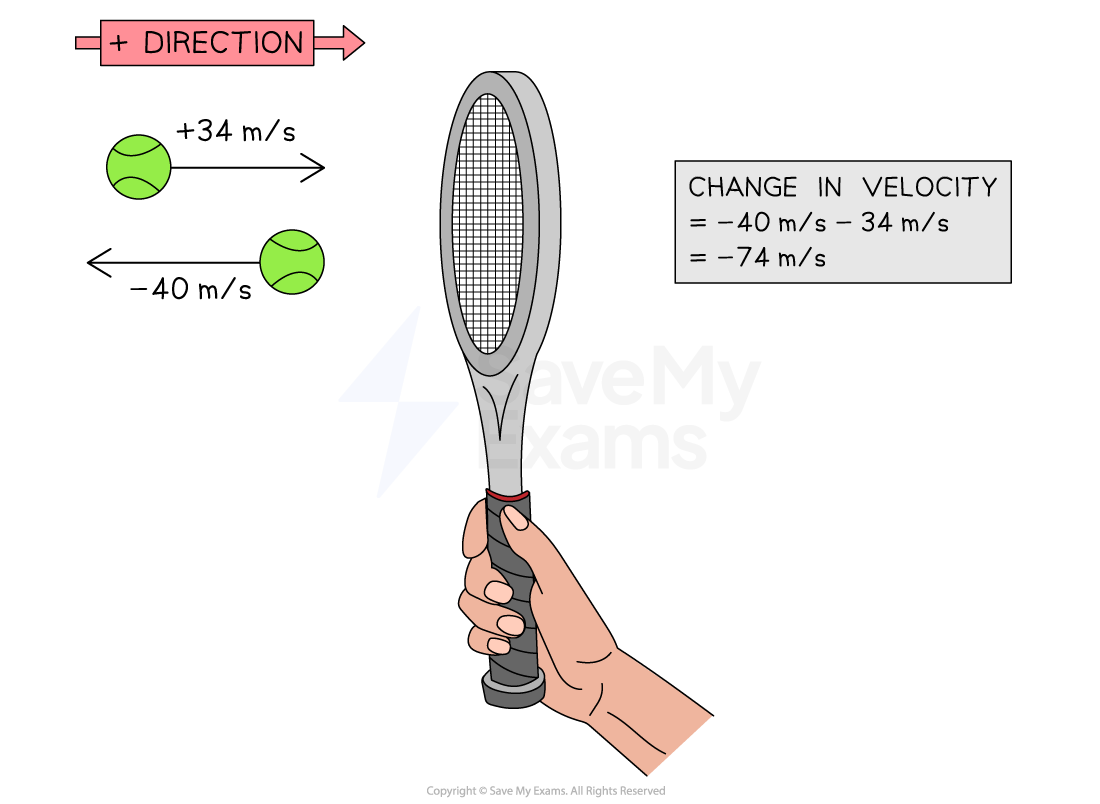
A professional tennis player hits a tennis ball of mass 60 g which travels at 34 m/s just before it makes contact with the racket. The ball is in contact with the racket for 5 ms before recoiling in the opposite direction at 40 m/s.

What is the average force exerted by the racket on the ball? Take the ball's initial velocity to be the positive direction.

A –888 N

B –72 N

C 72 N

D 888 N

The correct answer is A

Answer:

Step 1: Analyze the scenario

When the tennis ball comes into contact with the racket, the racket exerts a force on the ball over a time interval of 5 ms
This force changes the ball's momentum by
- decelerating it from 34 m/s to 0 m/s in the positive direction
- accelerating it from 0 m/s to 40 m/s in the opposite (negative) direction

Diagram showing a tennis ball before and after hitting a racket. Ball changes from +34 m/s to -40 m/s. Change in velocity calculated as -74 m/s.

Step 2: List the known quantities

Mass of the ball, $m$ = 60 g = 0.06 kg
Time interval, $∆ t$ = 5 ms = 0.005 s
Initial velocity, ${\vec{v}}_{0}$ = +34 m/s (positive direction)
Final velocity, $\vec{v}$ = –40 m/s (negative direction)

Step 3: Determine an expression for the average force

Since force is equal to the rate of change of momentum:

$\vec{F} = \frac{∆ \vec{p}}{∆ t} = \frac{m ∆ \vec{v}}{∆ t} = \frac{m (\vec{v} - {\vec{v}}_{0})}{∆ t}$

Step 4: Calculate the average force

$\vec{F} = \frac{0.06 \times (- 40 - 34)}{0.005} = - 888 N$

The answer is therefore A

Examiner Tips and Tricks

Be aware that multiple-choice options are designed to catch you out, so you need to be especially careful when vector quantities are involved! If an object changes direction, this must be reflected by the change in the sign of the velocity (and momentum).

Sometimes it can help to do a sense check, for example, in the worked example above, the ball's change in speed is (40 - 34) = 6 m/s, whereas the ball's change in velocity is (-40 - 34) = -74 m/s

The large magnitude reflects the fact that the ball's speed reduced to zero in the positive direction before it increased in the negative direction
The negative sign indicates the ball's final velocity is in the opposite direction to its initial velocity

Last updated: 22 September 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Linear MomentumNext:Impulse Equation