Impulse–Momentum Theorem (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Katie M

Expertise

Physics

Impulse–momentum theorem

In terms of momentum, Newton’s first law states:

The momentum of an object remains constant unless an external net force acts upon it

An impulse is exerted when an external force is applied for a time
Therefore, it must also change the linear momentum of the system
- This is known as the impulse-momentum theorem
The impulse-momentum theorem states that the impulse exerted on a system is equal to the change in momentum

$\vec{J} = {\vec{F}}_{a v g} ∆ t = ∆ \vec{p}$

Where:
- $\vec{J}$ = impulse, measured in $N \cdot s$
- ${\vec{F}}_{a v g}$ = average force exerted, measured in $N$
- $∆ t$ = time interval over which the force acts, measured in $s$
- $∆ \vec{p}$ = change in momentum, measured in $kg \cdot m / s$

In calculations, a more useful form of this equation is

$\vec{J} = {\vec{F}}_{a v g} ∆ t = m (\vec{v} - {\vec{v}}_{0})$

Where:
- $m$ = mass of the body, measured in $kg$
- $\vec{v}$ = final velocity, measured in $m / s$
- ${\vec{v}}_{0}$ = initial velocity, measured in $m / s$
Newton’s second law of motion is a direct result of the impulse-momentum theorem applied to systems with constant mass

${\vec{F}}_{n e t} = \frac{∆ \vec{p}}{∆ t} = m \frac{∆ \vec{v}}{∆ t} = m \vec{a}$

Where:
- $∆ \vec{v}$ = change in velocity, measured in $m / s$
- $\vec{a}$ = acceleration, measured in $m / s^{2}$
The impulse-momentum theorem tells us
- for a given change in momentum, a small force acting over a long time has the same effect as a large force acting over a short time
- for a constant force, applying the force over a longer time will lead to a greater change in momentum
- for a specified time, a greater force will lead to a greater change in momentum

Worked Example

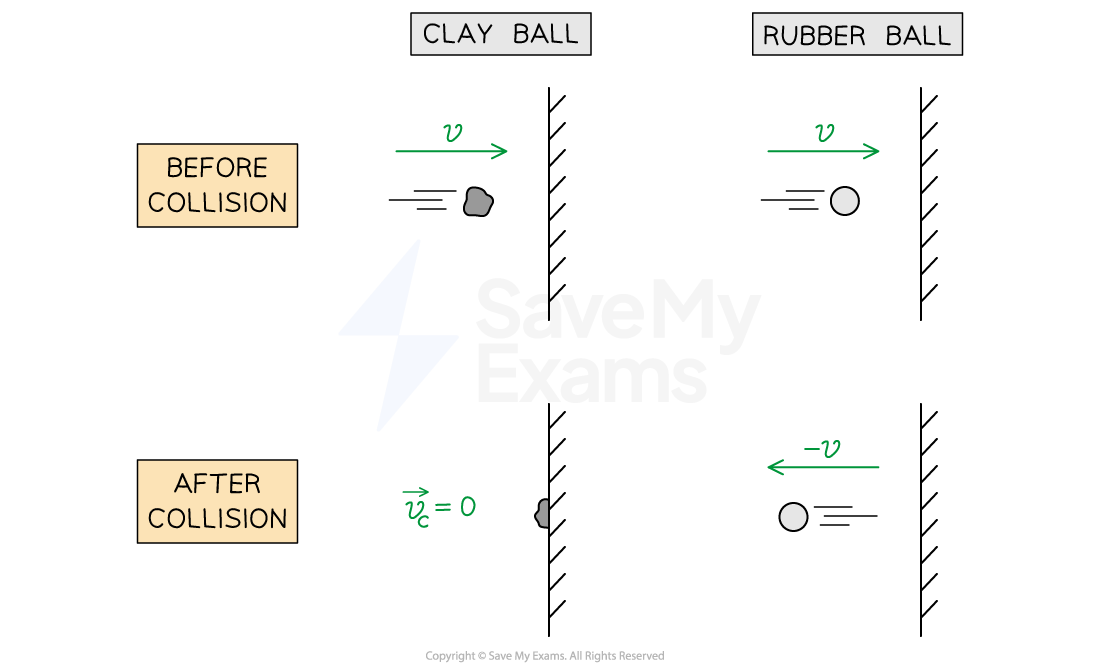
A rubber ball and a clay ball of the same mass are thrown horizontally at a wall. The rubber ball bounces off horizontally with the same speed it hits the wall. The clay ball strikes the wall and sticks to it.

If the impulse delivered to the rubber ball is ${\vec{J}}_{r}$ and the impulse delivered to the clay ball is ${\vec{J}}_{c}$ , what is the value of $\frac{{\vec{J}}_{r}}{{\vec{J}}_{c}}$ ?

A $- 2$

B $- \frac{1}{2}$

C $+ \frac{1}{2}$

D $+ 2$

The correct answer is D

Answer:

Step 1: Analyze the scenario

Initially, both balls travel:
- in the same direction, which we can define as the positive direction
- with the same velocity, which we can define as $v$
The rubber ball bounces off the wall, meaning:
- it travels in the opposite direction, so its final velocity is $- v$
- its momentum becomes negative
The clay ball sticks to the wall, meaning:
- it comes to rest, so its final velocity is zero
- its momentum becomes zero

Diagram showing a clay ball and a rubber ball before and after collision with a wall. The clay ball stops after collision, while the rubber ball bounces back at speed v.

Step 2: Determine the impulse delivered to each object

The impulse delivered to an object is its change in momentum

$\vec{J} = ∆ \vec{p} = m ∆ \vec{v}$

The impulse delivered to the rubber ball is

${\vec{J}}_{r} = ∆ {\vec{p}}_{r} = - m v - m v = - 2 m v$

The impulse delivered to the clay ball is

${\vec{J}}_{c} = ∆ {\vec{p}}_{c} = 0 - m v = - m v$

Step 3: Determine the ratio of the impulses

The ratio of the impulse delivered to the rubber ball to that of the clay ball is:

$\frac{{\vec{J}}_{r}}{{\vec{J}}_{c}} = \frac{∆ {\vec{p}}_{r}}{∆ {\vec{p}}_{c}} = \frac{- 2 m v}{- m v} = 2$

Worked Example

Car X is designed to include a crumple zone so that the front of the car collapses during impact. A similar car, Y, is designed without a crumple zone.

Both cars undergo a safety test in which they are driven into a solid concrete wall at the same speed. Analysis of the crash shows that the front of Car X collapses by 1.40 m, while the front of Car Y collapses by 15.0 cm.

(A) Is the change in momentum of Car X greater than, less than, or the same as the change in momentum of Car Y? Justify your answer.

(B) Is the average force on Car X greater than, less than, or the same as the average force on Car Y? Justify your answer.

(C) Is the time taken for Car X to come to rest greater than, less than, or the same as the time taken for Car Y to come to rest? Justify your answer.

(D) Use the information provided to justify whether crumple zones make cars safer in the event of a collision.

Answer:

Part (A)

Step 1: Analyze the scenario

The change in momentum is equal to the product of the mass and the change in velocity

$∆ \vec{p} = m ∆ \vec{v} = m (\vec{v} - {\vec{v}}_{0})$

The final velocity of both cars is zero, so the change in momentum depends on the initial momentum of the car only

$∆ \vec{p} = m (0 - v_{0}) = - m v_{0}$

Step 2: Deduce and justify the relationship

The change in momentum of Car X is the same as the change in momentum of Car Y
Justification:
- Both cars have the same mass and initial velocity
- Therefore, $∆ {\vec{p}}_{X} = ∆ {\vec{p}}_{Y}$

Part (B)

Step 1: Analyze the scenario

According to the Work-Energy Theorem, the change in kinetic energy equals the work required to stop the car

$∆ K = W = \frac{1}{2} m (v^{2} - {v_{0}}^{2})$

The work done is equal to the product of the average force on the car and the distance moved while the force is applied

$W = F_{a v g} d = \frac{1}{2} m (0 - {v_{0}}^{2}) = - \frac{1}{2} m {v_{0}}^{2}$

The average force on the car is therefore equal to

$F_{a v g} = - \frac{m {v_{0}}^{2}}{2 d}$

During the collision, the front of the car collapses, so the distance $d$ is equal to the length of material that deforms

Step 2: Deduce and justify the relationship

The average force on Car X is less than the average force on Car Y
Justification:
- The front of Car X collapses by $d_{X} = 1.40 m$ whereas Car Y collapses by $d_{Y} = 0.15 m$
- Therefore, Car X stops over a greater distance than Car Y, by a factor of $\frac{d_{X}}{d_{Y}} = \frac{1.40}{0.15} = 9.3$
- Both cars have the same mass and initial speed
- Therefore, the force on Car X is smaller than the force on Car Y by a factor of $\frac{F_{X}}{F_{Y}} = \frac{d_{Y}}{d_{X}} = \frac{0.15}{1.40} = 0.11$

Part (C)

Step 1: Analyze the scenario

According to the Impulse-Momentum Theorem, the change in momentum is equal to the product of the net external force and the amount of time that the force is exerted

$∆ \vec{p} = {\vec{F}}_{a v g} ∆ t$

For a given change in momentum, the greater the net external force on a car, the shorter the collision time

Step 2: Deduce and justify the relationship

The time taken for Car X to come to rest is greater than the time taken for Car Y to come to rest
Justification:
- In part (A), we established the change in momentum is the same for both cars
- In part (B), we established Car X experiences a smaller average force than Car Y
- Therefore, Car X stops over a longer time than Car Y, by a factor of $\frac{∆ t_{X}}{∆ t_{Y}} = \frac{F_{Y}}{F_{X}} = \frac{1.40}{0.15} = 9.3$

Part (D)

Step 1: Analyze the scenario

As the car comes to a stop over the time period $∆ t$ , the driver will continue moving forward at the same speed $v_{0}$ as the car before the crash, unless they are wearing a seatbelt
Assuming this is the case, the average force exerted by the seat belt on the driver is equal to the rate of change of momentum of the driver

${\vec{F}}_{a v g} = \frac{∆ \vec{p}}{∆ t} = - \frac{m v_{0}}{∆ t}$

Where $m$ is the mass of the driver

Step 2: Write a conclusion and justification for your claim

Crumple zones do make cars safer in the event of a collision
Justification:
- The car with the crumple zone (Car X) was shown to increase both the distance and the time over which the collision occurred by a factor of 9.3 when compared to the car without a crumple zone (Car Y)
- As a result, the force on the car, and therefore the driver, in Car X was about 9.3 times lower than the force on the driver in Car Y
- This suggests the likelihood of injury is much lower in cars which have crumple zones

Examiner Tip

Most practical applications of the impulse-momentum theorem involve a change in velocity with respect to time. In AP Physics 1, you will not be required to analyze systems where mass changes with respect to time quantitatively (i.e. involving calculations), but you could be asked to analyze such a system qualitatively. This could involve discussing proportionality relationships between the changing mass and another quantity, such as a change in momentum, force, or time.

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

Impulse–Momentum Theorem (College Board AP® Physics 1: Algebra-Based)

Study Guide

Impulse–momentum theorem

Worked Example

Worked Example

Examiner Tip

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M