Impulse Graphs (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Written by: Katie M

Reviewed by: Caroline Carroll

Force-time graph

In real-life scenarios, forces are often not constant and will vary over time
A changing force can be plotted as a function of time
The impulse delivered to a system is equal to the product of force and time
Therefore, the area under the force-time graph is equal to
- impulse
- change in momentum

$area = {\vec{F}}_{a v g} ∆ t = \vec{J} = ∆ \vec{p}$

Determining impulse from a force-time graph

Graph of force in newtons (N) against time in seconds (s) with a label indicating that the area under the curve represents the impulse in newton seconds (N s). — **When a net external force varies with time, the impulse delivered to the system can be found from the area under the force-time graph**

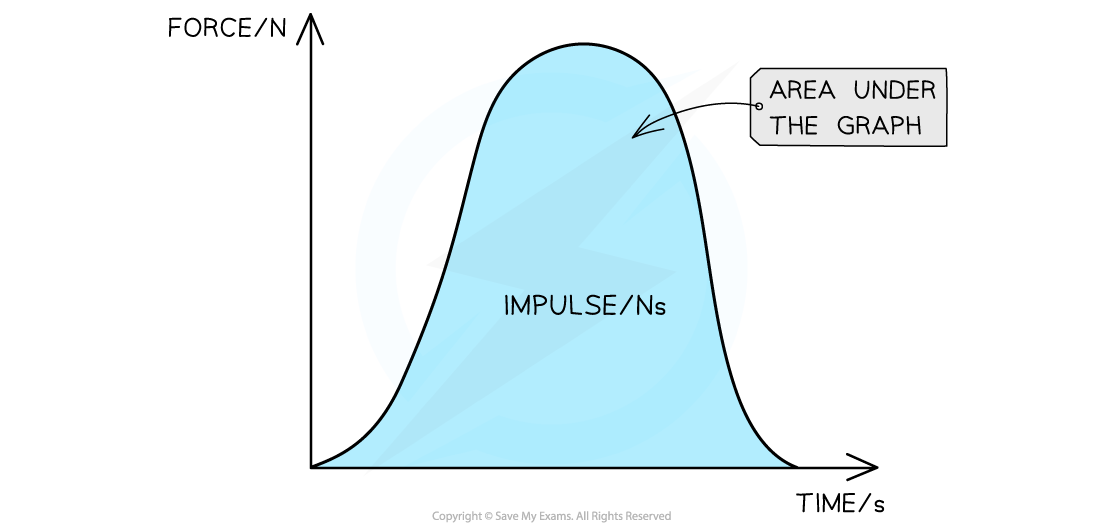
Comparing impulse using force-time graphs

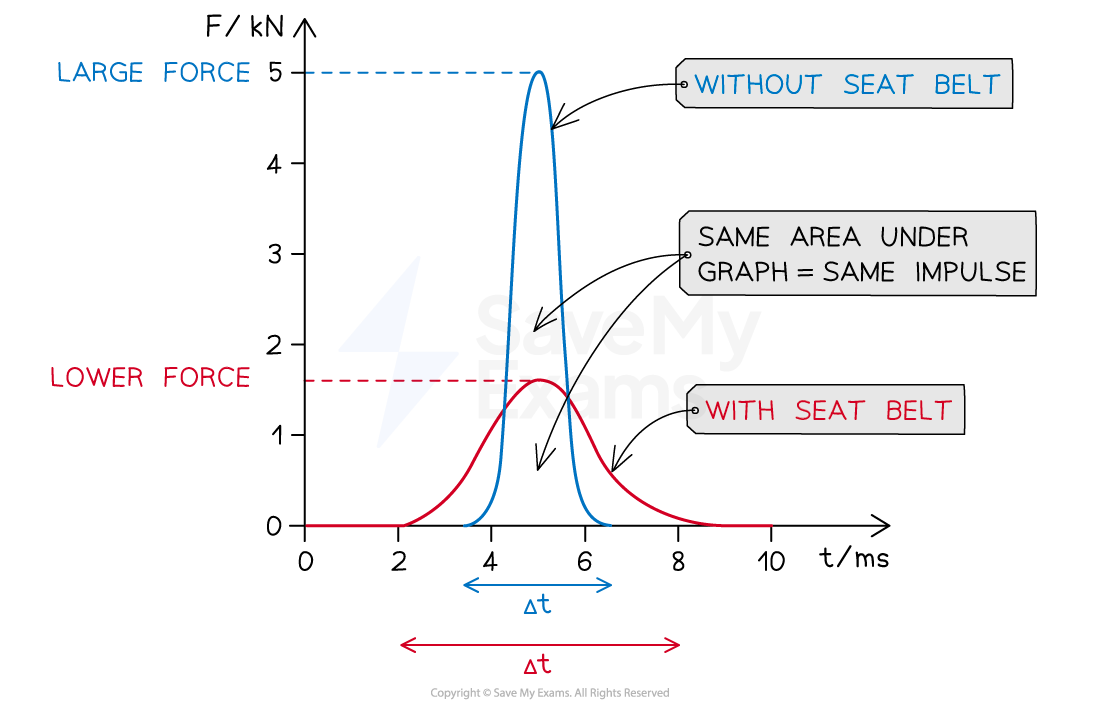
In a collision, the force of an impact can be reduced by increasing the contact time over which the collision occurs
- For example, cars include seatbelts which are able to stretch and increase the collision time
In a vehicle collision, if the passenger is not wearing a seat belt, they will experience
- a larger maximum force
- a shorter collision time
If the passenger is wearing a seat belt, they will experience
- a lower maximum force
- a longer collision time
On a force-time graph:
- the case of a passenger not wearing a seat belt is represented by a higher peak and narrower base
- the case of a passenger wearing a seat belt is represented by a lower peak and wider base
Since the change in momentum (impulse) is the same for both cases, the area under the curves is the same

Force-time graphs for a vehicle collision

Graph comparing force over time with and without a seat belt. The curve for the collision "without seat belt" shows a higher peak force and a shorter collision time. The curve for the collision "with seat belt" shows a lower peak force and a longer collision time. The area under both graphs is the same indicating the impulse is the same in both cases. — **The increase in contact time decreases the impact force for the same impulse, which can be seen on a force-time graph where the area under both curves is the same**

Worked Example

The graph shows the force applied to an object of mass $2 kg$ as a function of time. The object has an initial velocity of $+ 2.5 m / s$ at t = 0.

Graph showing force F in newtons (N) against time in seconds (s). Between t = 0 and t = 1 s, the force is zero. Between t = 1 s and t = 2 s, the force increases from 0.0 to 3.0 N. Between t = 2 s and t = 3 s, the force decreases from 3.0 N to -1.0 N. Between t = 1 s and t = 2 s, the force has a constant value of -1.0 N.

(A) What is the impulse delivered to the object from t = 1 to t = 3 s?

(B) What is the velocity of the object at t = 4 s?

Answer:

Part (A)

Step 1: Analyze the scenario

From t = 1 to t = 2 s, the force increases to a maximum of 3.0 N and then, from t = 2 s to t = 3 s decreases to a minimum of -1.0 N
At approximately t = 2.7 s, the direction of the applied force changes
The impulse delivered to the object from t = 1 to t = 3 s is equal to the area under the graph between these times

Step 2: Determine the impulse delivered between t = 1 to t = 3 s

The impulse is the area under the graph. The graph can be split up into three right-angled triangles

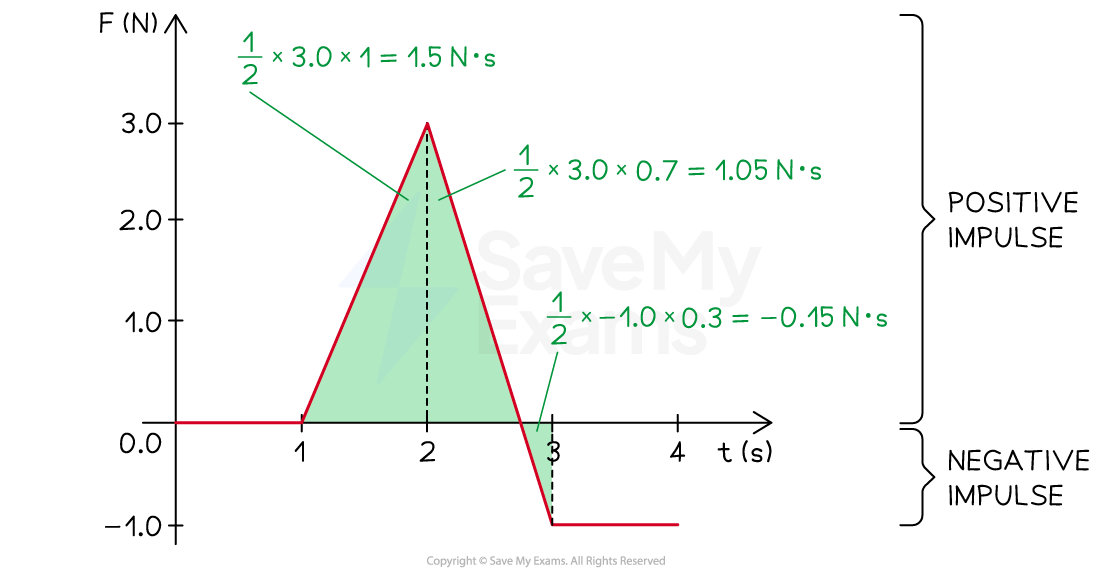
Graph showing force F in newtons (N) against time in seconds (s). Between t = 1 s and t = 2 s, the force increases from 0 to 3.0 N, and the area under gives an impulse of 1/2 × 3.0 × 1 = 1.5 N⋅s. Between t = 2 s and t = 2.7 s, the force decreases from 3.0 N to 0, and the area under gives an impulse of 1/2 × 3.0 × 0.7 = 1.05 N⋅s. Between t = 2.7 s and t = 3 s, the force decreases from 0 to -1.0 N, the area under gives an impulse of 1/2 × -1.0 × 0.3 = -0.15 N⋅s

Remember that when the graph is negative, the area is also negative

$\vec{J} = (\frac{1}{2} \times 3.0 \times 1) + (\frac{1}{2} \times 3.0 \times 0.7) - (\frac{1}{2} \times 1.0 \times 0.3)$

$\vec{J} = 1.5 + 1.05 - 0.15 = 2.4 N \cdot s$

Part (B)

Step 1: Analyze the scenario

The impulse delivered to the object over the 4 s interval changes its momentum
From t = 0 to t = 1 s, no forces act, hence no impulse is delivered, so the velocity at t = 1 s is still +2.5 m/s
From t = 1 to t = 3 s, the impulse delivered to the object is 2.4 N⋅s
From t = 3 to t = 4 s, the impulse delivered to the object is equal to the area under the graph in this interval

Step 2: Determine the total impulse delivered over the 4 s interval

The impulse delivered between t = 3 to t = 4 s is the area under the graph

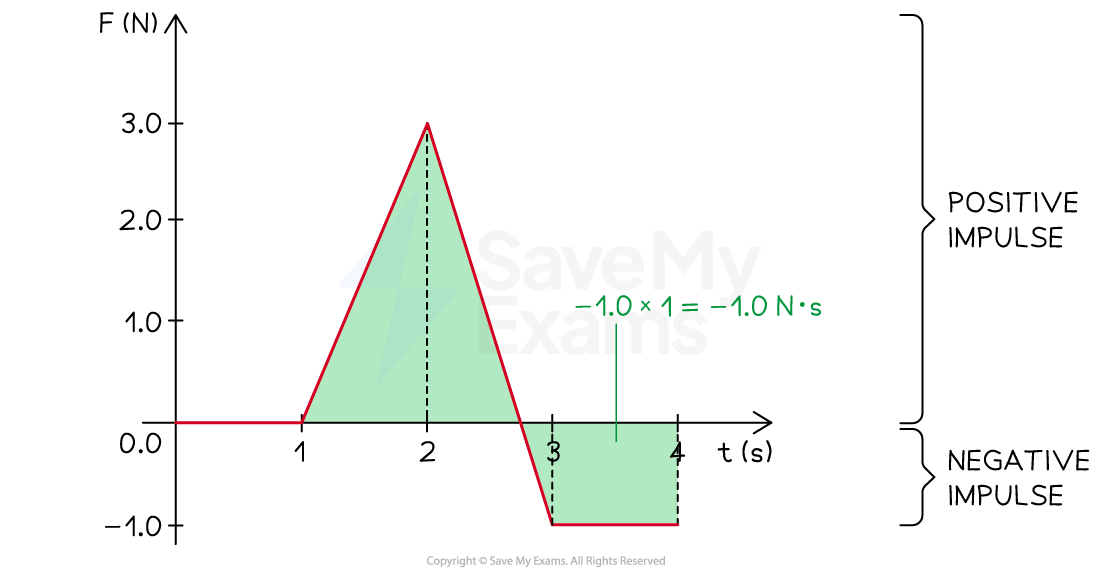
Graph showing force F in newtons (N) against time in seconds (s). Between t = 0 and t = 1 s, the force is 0 N. Between t = 3 s and t = 4 s, the force has a constant value of -1.0 N, and the area under gives an impulse of -1.0 × 1 = -1.0 N⋅s

The total impulse delivered between t = 0 and t = 4 s is:

$\vec{J} = 2.4 - (1.0 \times 1) = 2.4 - 1.0 = 1.4 N \cdot s$

Step 3: Determine the final velocity of the object

The impulse changes the momentum and velocity of the object

$\vec{J} = ∆ \vec{p} = m (\vec{v} - {\vec{v}}_{0})$

Where $m$ = 2 kg and ${\vec{v}}_{0}$ = +2.5 m/s, therefore, at t = 4 s:

$1.4 = 2 \times (\vec{v} - 2.5)$

$\vec{v} = 3.2 m / s$

Worked Example

A horizontal force is applied to a 5 kg box which is initially at rest. The box begins to move along a frictionless horizontal surface. The graph shows the magnitude of the force as a function of time.

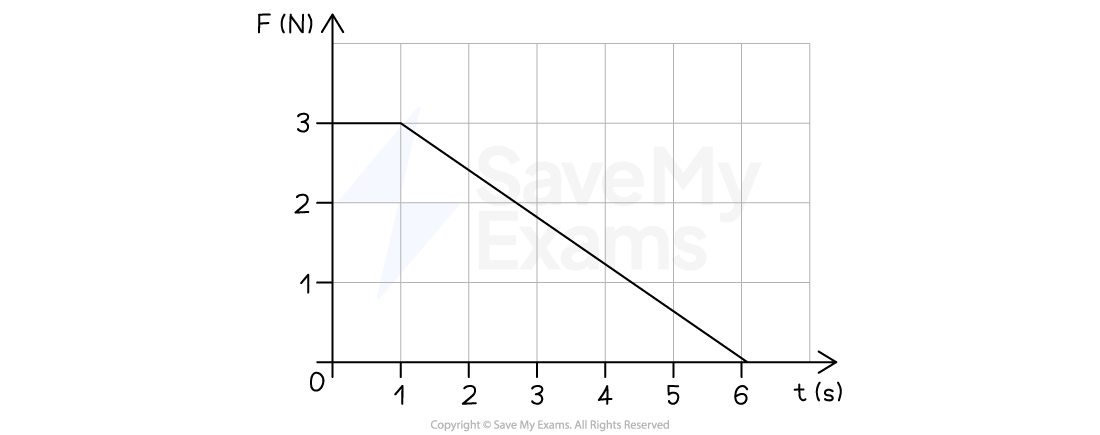
Graph showing force in newtons (N) against time in seconds (s). From t = 0 s to t = 1 s, force has a constant value of 3 N. From t = 1 s to t = 6 s, force decreases linearly from 3 N to 0 N

(A) In which 1-second interval is the impulse applied to the box the greatest? Explain your reasoning.

(B) Using the graph, plot the momentum as a function of time.

Answer:

Part (A)

Step 1: Identify the interval the impulse has the greatest magnitude

The impulse has the greatest magnitude during the interval t = 0 to t = 1 s

Step 2: Give a justification for your answer

Impulse is equal to the area under the force-time graph
Therefore, the larger the area, the greater the magnitude of the impulse

Part (B)

Step 1: Analyze the scenario

The force applied to the box has a constant value of 3 N in the interval t = 0 s to t = 1 s
During this time, momentum increases at a constant rate
The force then decreases linearly from 3 N to 0 N in the interval t = 1 s to t = 6 s
During this time, momentum continues to increase at a decreasing rate

Step 2: Determine the change in momentum in each interval

Impulse, or change in momentum, is equal to the area under the force-time graph

$∆ p = F ∆ t$

The box is initially at rest, so the momentum is initially zero

Time (s)	Change in momentum (kg∙m/s)	Momentum (kg∙m/s)
0	0	0
1	3.0	3.0
2	2.7	5.7
3	2.1	7.8
4	1.5	9.3
5	0.9	10.2
6	0.3	10.5

Step 3: Plot the momentum-time graph

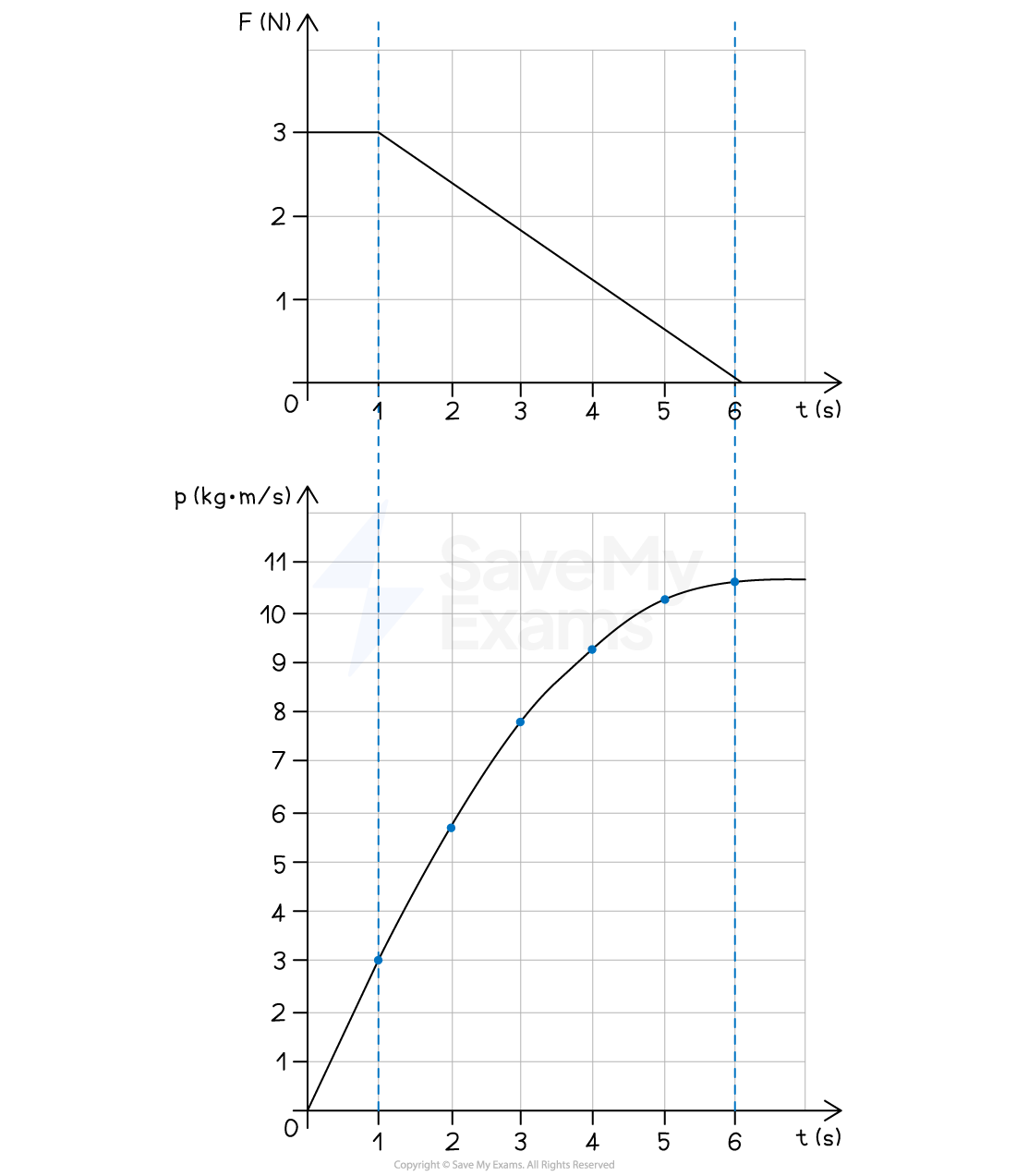
Two graphs: the top graph shows force (F) decreasing linearly from 3 N to 0 N over 6 seconds; the bottom graph shows momentum (p) increasing non-linearly, leveling at 11 kg∙m/s by 6 seconds.

Part (C)

Step 1: List the known quantities

Mass of the box, $m = 5 kg$
Initial velocity, ${\vec{v}}_{0} = 0$
From the graph, the change in momentum (between t = 0 and t = 6 s) is equal to $∆ \vec{p} = 10.5 kg \cdot m / s$

Step 2: Write an expression for the change in momentum

The change in momentum is equal to the product of the mass and the change in velocity

$∆ \vec{p} = m ∆ \vec{v} = m (\vec{v} - {\vec{v}}_{0})$

Step 3: Determine the final velocity of the object

$10.5 = 5 \times (\vec{v} - 0) = 5 \vec{v}$

$\vec{v} = 2.1 m / s$

Examiner Tips and Tricks

The shape of a force-time graph may be curved or straight

If the graph is a curve, the area can be found by counting the squares or approximating the areas using basic shapes
If the graph is made up of straight lines, split the graph into sections. The total area is the sum of the areas of each section

Momentum-time graph

A changing momentum can be plotted as a function of time
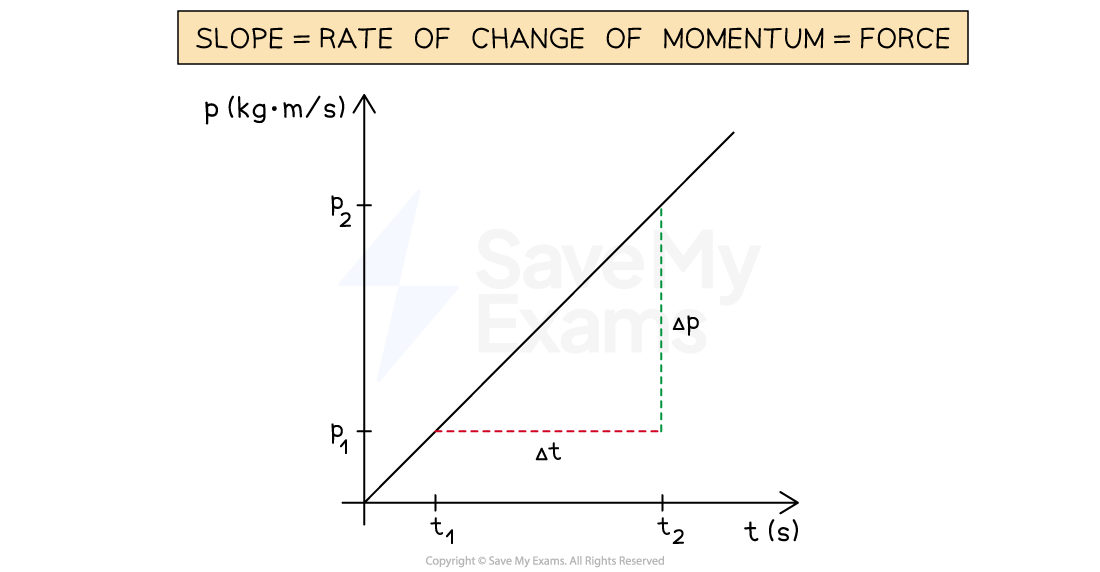
The net external force exerted on a system is equal to the rate of change of momentum
Therefore, force is equal to the slope of a momentum-time graph

$slope = \frac{{\vec{p}}_{2} - {\vec{p}}_{1}}{t_{2} - t_{1}} = \frac{∆ \vec{p}}{∆ t} = {\vec{F}}_{n e t}$

Determining force from a momentum-time graph

Graph of momentum in kg·m/s against time in s, with a label indicating that the slope represents the force — **When momentum varies with time, the net external force exerted on the system can be found from the slope of the momentum-time graph**

Translating between force and momentum graphs

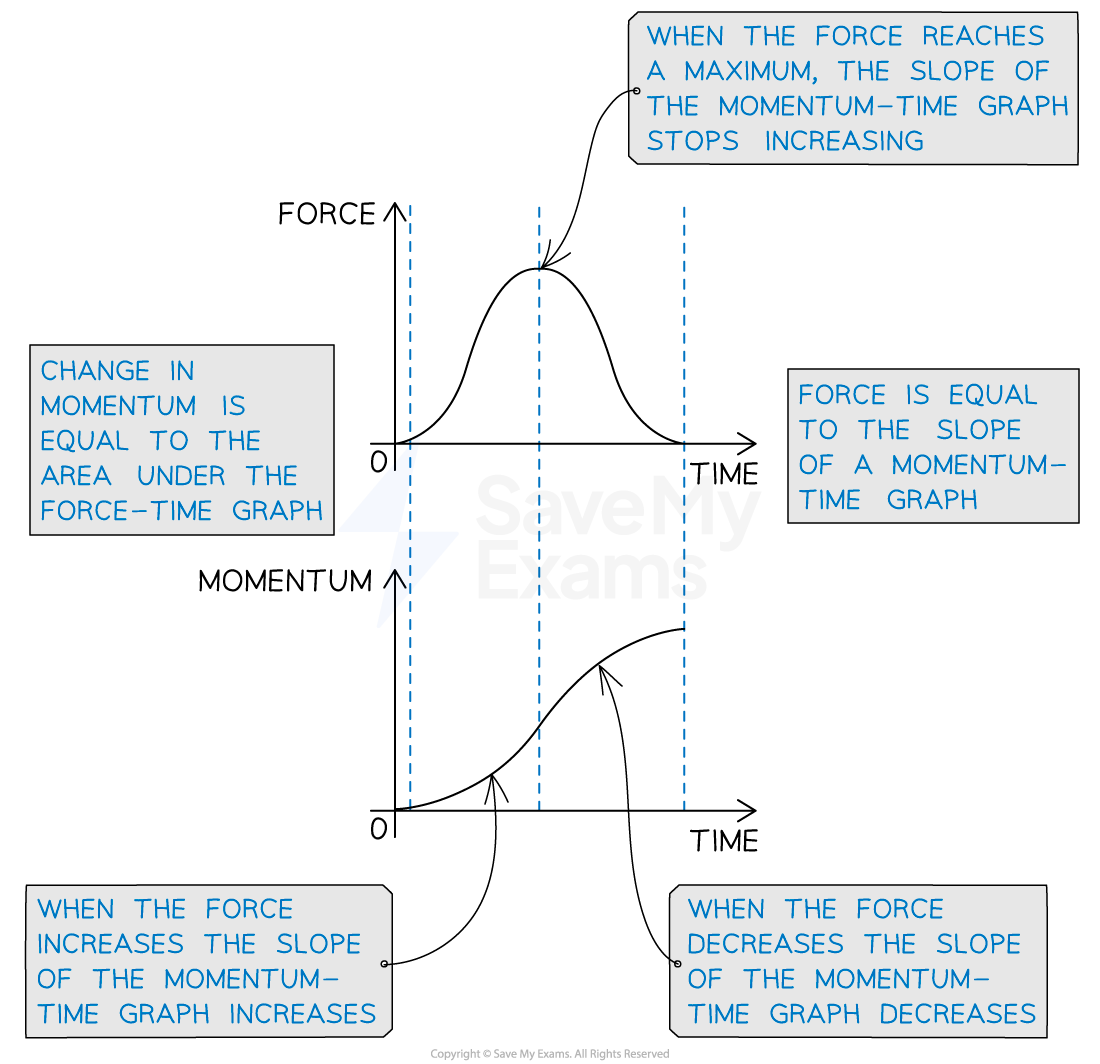
A momentum-time graph can be plotted from a force-time graph by
- splitting the force-time graph up into sections
- calculating the area (impulse, or change in momentum) of each section
- plotting the values of momentum in each time interval
A force-time graph can be plotted from a momentum-time graph by
- splitting the momentum-time graph up into sections
- calculating the slope (force) of each section
- plotting the values of force in each time interval

Relationship between a force-time graph and a momentum-time graph

The top graph shows force against time and the bottom graph shows momentum against time. Dotted lines show corresponding sections of the graphs and the text explains the relationships between the force-time graph and the momentum-time graph. — **A force-time graph can be translated into a momentum-time graph, and vice versa, by applying the relationship between force and momentum**

Examiner Tips and Tricks

Being able to find the area under a curve, or the slope of a line, and then relating them to physical quantities is an extremely important skill in physics. A more advanced skill is then being able to translate between graphs of related quantities.

Since $\vec{F} \propto \vec{a}$ and $\vec{p} \propto \vec{v}$ , force and momentum graphs can be translated in the same way as acceleration and velocity graphs. For example, acceleration is equal to the slope of a velocity-time graph

momentum-time graph

slope = force $(\vec{F})$

force-time graph

area = impulse $(\vec{J})$

velocity-time graph

slope = acceleration $(\vec{a})$

acceleration-time graph

area = velocity $(\vec{v})$

Last updated: 3 September 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Impulse–Momentum TheoremNext:The Principle of Conservation of Momentum

Impulse Graphs (College Board AP® Physics 1: Algebra-Based)

Study Guide

Force-time graph

Determining impulse from a force-time graph

Comparing impulse using force-time graphs

Force-time graphs for a vehicle collision

Worked Example

Worked Example

Examiner Tips and Tricks

Momentum-time graph

Determining force from a momentum-time graph

Translating between force and momentum graphs

Relationship between a force-time graph and a momentum-time graph

Examiner Tips and Tricks

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M

Author: Caroline Carroll