The Principle of Conservation of Momentum (College Board AP® Physics 1: Algebra-Based) : Study Guide

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on 11 March 2025

The principle of conservation of linear momentum

Momentum, like energy, is conserved in all interactions
This is known as the principle of conservation of momentum, which states that:

The total linear momentum of an isolated system remains constant unless acted on by a net external force

Therefore, for an interaction between objects in an isolated system:

The total momentum before the interaction is equal to the total momentum after the interaction

Mathematically, this can be written as:

$\sum {\vec{p}}_{i} = \sum {\vec{p}}_{f}$

Where:
- ${\vec{p}}_{i}$ = initial momentum (before the interaction), in $kg \cdot m / s$
- ${\vec{p}}_{f}$ = final momentum (after the interaction), in $kg \cdot m / s$
Since momentum is a vector quantity, the vector sum $(\sum)$ of the momenta of the components of the system remains constant

$m_{1} {\vec{v}}_{i 1} + m_{2} {\vec{v}}_{i 2} = m_{1} {\vec{v}}_{f 1} + m_{2} {\vec{v}}_{f 2}$

Where:
- $m_{1}$ = mass of object 1, in $kg$
- $m_{2}$ = mass of object 2, in $kg$
- ${\vec{v}}_{i 1}$ = initial velocity of object 1, in $m / s$
- ${\vec{v}}_{i 2}$ = initial velocity of object 2, in $m / s$
- ${\vec{v}}_{f 1}$ = final velocity of object 1, in $m / s$
- ${\vec{v}}_{f 2}$ = final velocity of object 2, in $m / s$

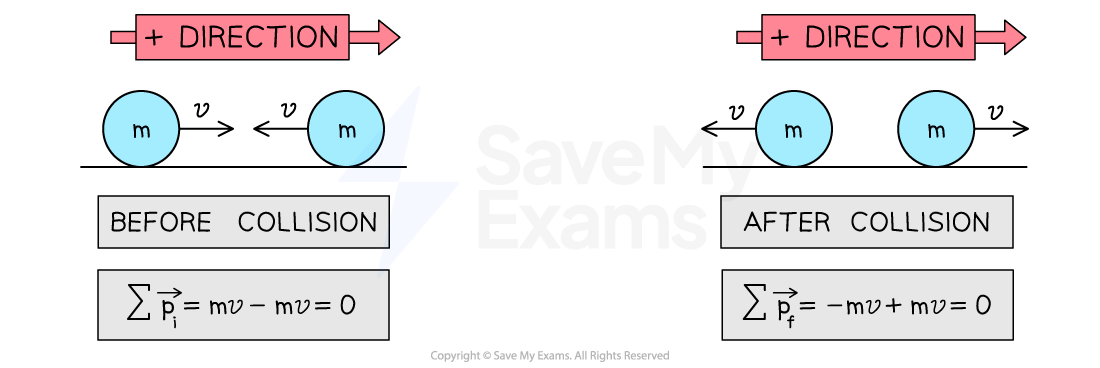
Example 1: two identical objects colliding

When two identical objects of mass $m$ travel towards each other at the same speed $v$
- the object moving in the positive direction has velocity $+ v$
- the object moving in the negative (opposite) direction has velocity $- v$
Applying the principle of conservation of momentum gives:

$m v - m v = - m v + m v$

The momentum vectors are equal in magnitude and opposite in direction
Therefore, they cancel each other out, resulting in a net momentum of zero

${\vec{p}}_{n e t} = 0$

Conservation of momentum between identical spheres

Two spheres of mass m collide head-on with equal velocities before and after collision. The direction of positive velocity is to the right. Equations show momentum conservation for both scenarios. — **The conservation of momentum for two spheres of equal mass m and velocity v. Assuming no energy is lost to the surroundings, they both rebound in opposite directions with the same speed**

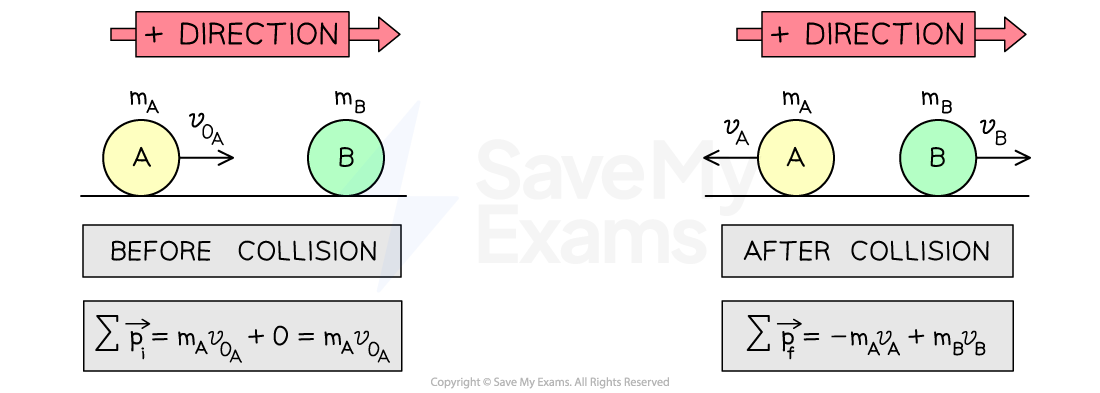
Example 2: two objects rebounding

When moving object A collides with stationary object B and rebounds
- object A has an initial velocity of $v_{0 A}$ and a final velocity of $- v_{A}$
- object B has an initial velocity of $0$ and a final velocity of $+ v_{B}$
Applying the principle of conservation of momentum gives:

$m_{A} v_{0 A} + 0 = - m_{A} v_{A} + m_{B} v_{B}$

Taking the direction of the initial motion of object A as the positive direction:
- Object A has a positive momentum before the collision and a negative momentum after
- Object B has zero momentum before the collision and positive momentum after
Therefore, the net momentum of the system is:

${\vec{p}}_{n e t} = m_{A} (v_{0 A} + v_{A}) - m_{B} v_{B}$

Conservation of momentum between non-identical spheres

A collision between two spheres, A and B. Before the collision, mass A moves to the right with initial velocity v0A towards a stationary mass B; after the collision, mass A moves to the left with final velocity vA, and mass B moves to the right with final velocity vB. — **The conservation of momentum for two spheres of unequal mass A and B. Sphere A collides with sphere B and they both rebound in opposite directions**

Worked Example

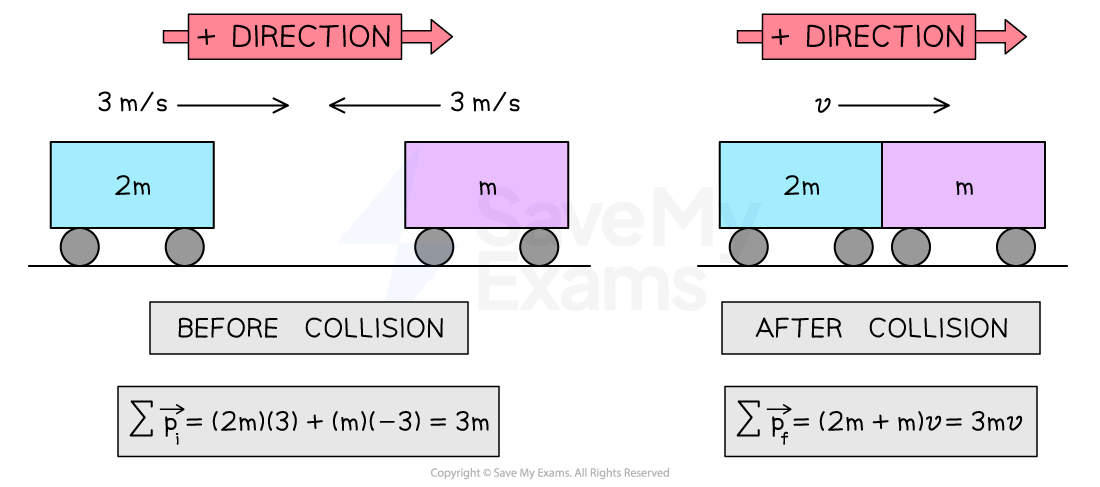
A trolley of mass $2 m$ and a trolley of mass $m$ approach each other, both trolleys have a speed of 3 m/s, as shown in the diagram.

Two trolleys move towards each other at equal speeds of 3 m/s. The blue trolley on the left has mass 2m and moves to the right and the purple trolley on the right has mass m and moves to the left.

When the trolleys collide head-on, they stick together and move away as one trolley.

Assuming positive momentum is to the right, which of the following is the best representation of the momentum of the trolleys as a function of time?

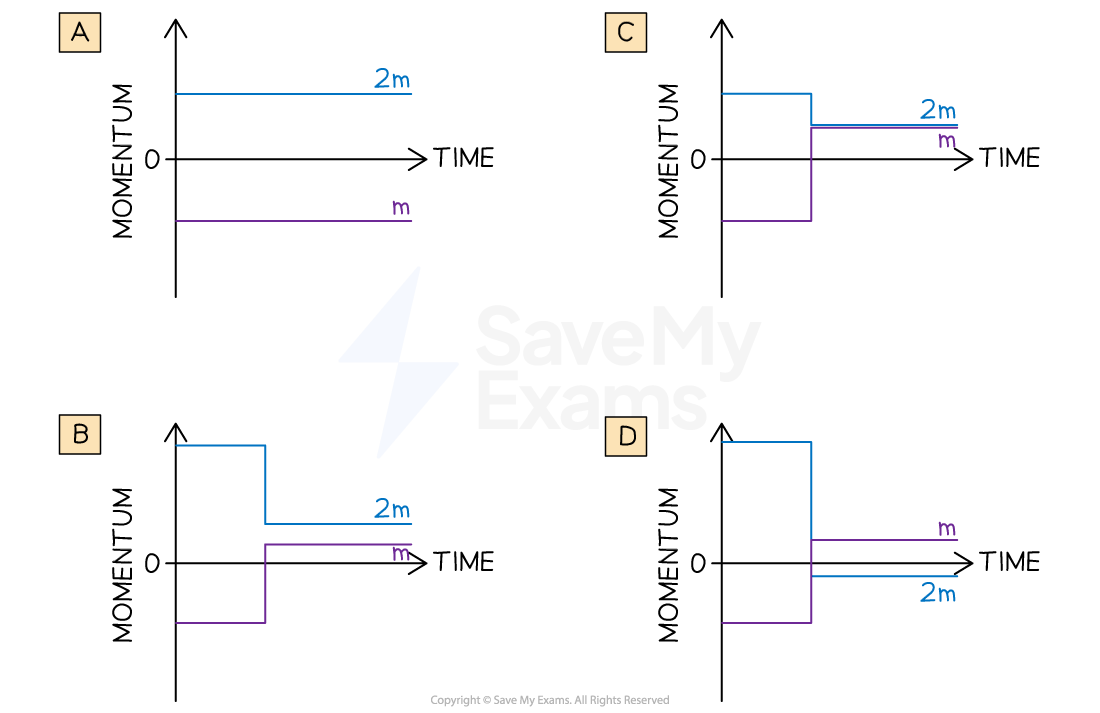
Four momentum vs. time graphs labeled A to D, with varying levels for 2m and m. The x-axis represents time, and the y-axis represents momentum.

The correct answer is B

Answer:

Step 1: Analyze the scenario

Before the collision, the trolleys move toward each other at the same speed, so one of the velocities will be negative
The positive direction is defined to the right, or in the direction the trolley with mass $2 m$ moves initially, so
- the trolley with mass $2 m$ has a positive velocity of $+ 3 m / s$
- the trolley with mass $m$ has a negative velocity of $- 3 m / s$
When the trolleys collide, they stick together and become a single trolley of mass $3 m$ with final velocity $v$
The trolleys move off together in the direction of the largest initial momentum, logically this must be the trolley with mass $2 m$

Two trolleys before and after a collision. The blue cart (2m) moves right at 3 m/s and the purple cart (m) moves left at 3 m/s before collision. They stick together after collision and move together with velocity v.

Step 2: Apply the principle of conservation of momentum

Conservation of momentum: the total momentum before the collision is equal to the total momentum after

$\sum {\vec{p}}_{i} = \sum {\vec{p}}_{f}$

$(2 m) (3) + (m) (- 3) = (2 m + m) v$

$3 m = 3 m v$

Therefore, the final velocity of the trolleys is

$v = \frac{3 m}{3 m} = 1 m / s$

Step 3: Sketch the momentum-time graph for each trolley

Before the collision:
- the trolley of mass $2 m$ has a momentum of $+ 6 m$
- the trolley of mass $m$ has a momentum of $- 3 m$

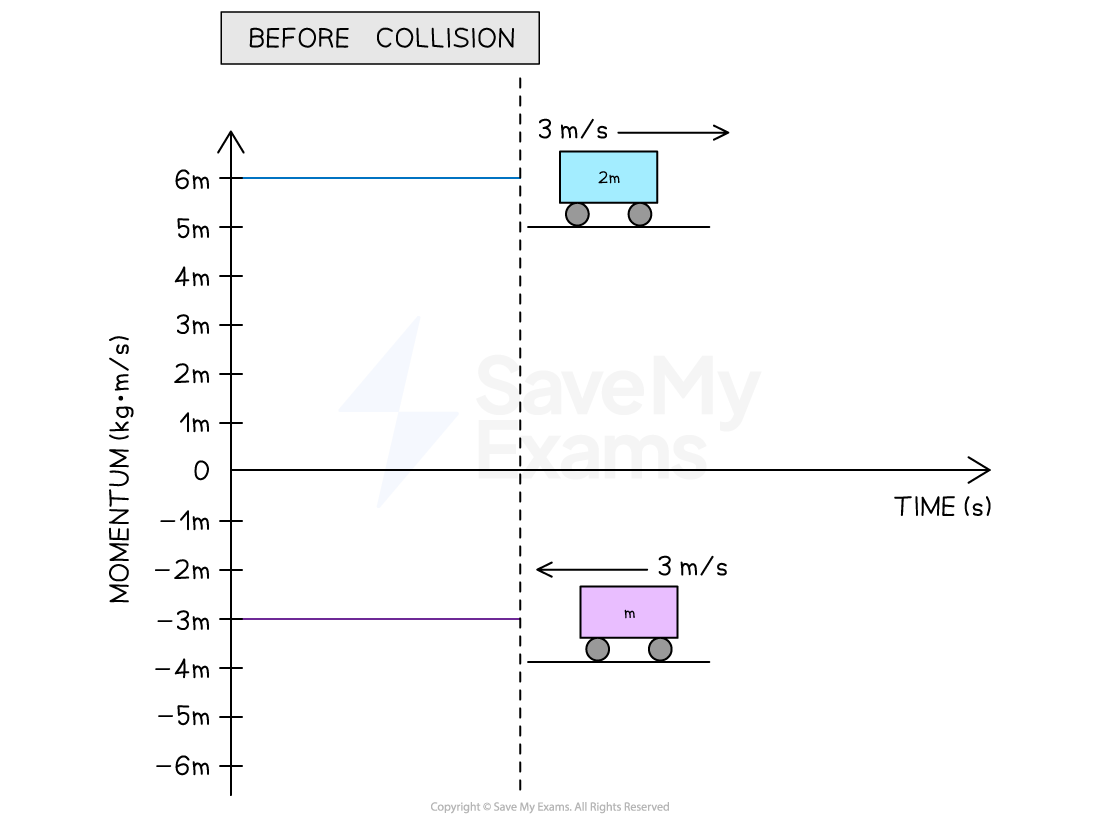
Graph showing momentum-time graph for the motion before the collision. A 2m cart moves right at 3 m/s (6 kg·m/s), while an m cart moves left at 3 m/s (-3 kg·m/s).

After the collision:
- the trolley of mass $2 m$ has a momentum of $+ 2 m$
- the trolley of mass $m$ has a momentum of $+ m$

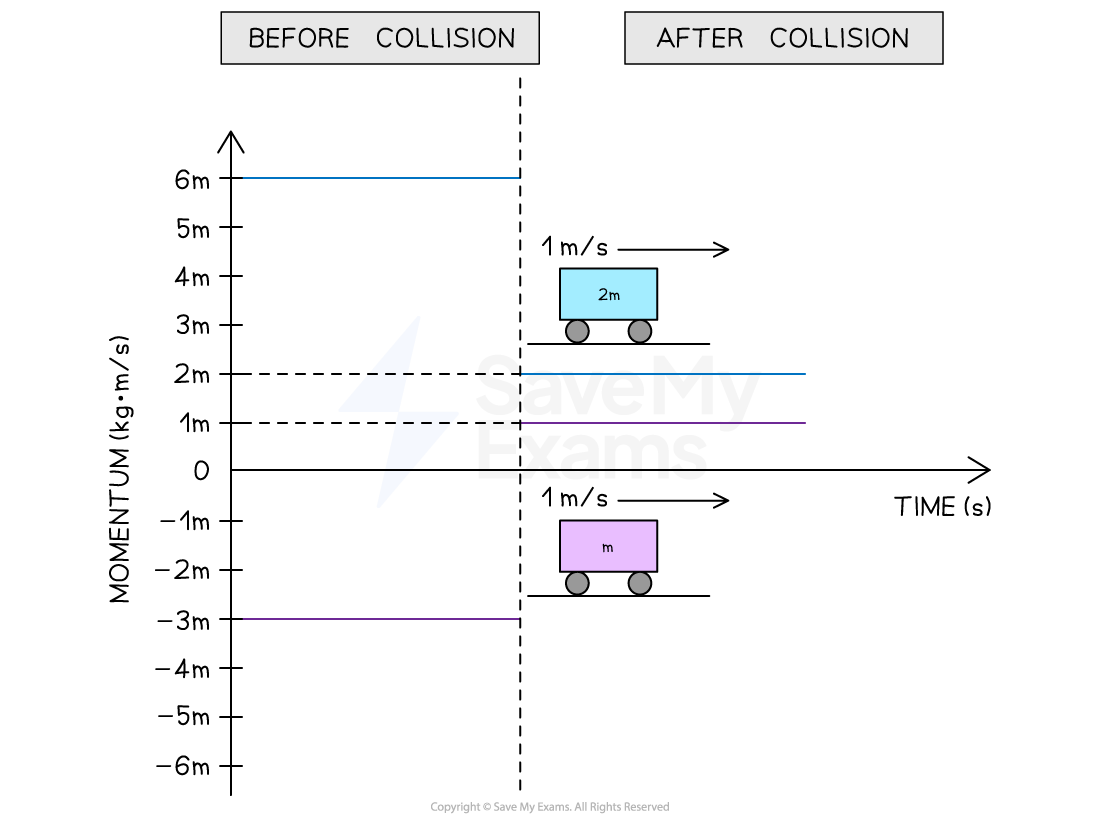
Graph showing momentum vs. time before and after a collision. Two carts labeled "2m" and "m" move at 1 m/s. Momentum values are shown from -6m to 6m kg·m/s.

Step 4: Connect the lines to show the change in momentum

The finished graph shows that the change in momentum (vertical line) is the same for both trolleys
This is not seen in graphs A, C, or D

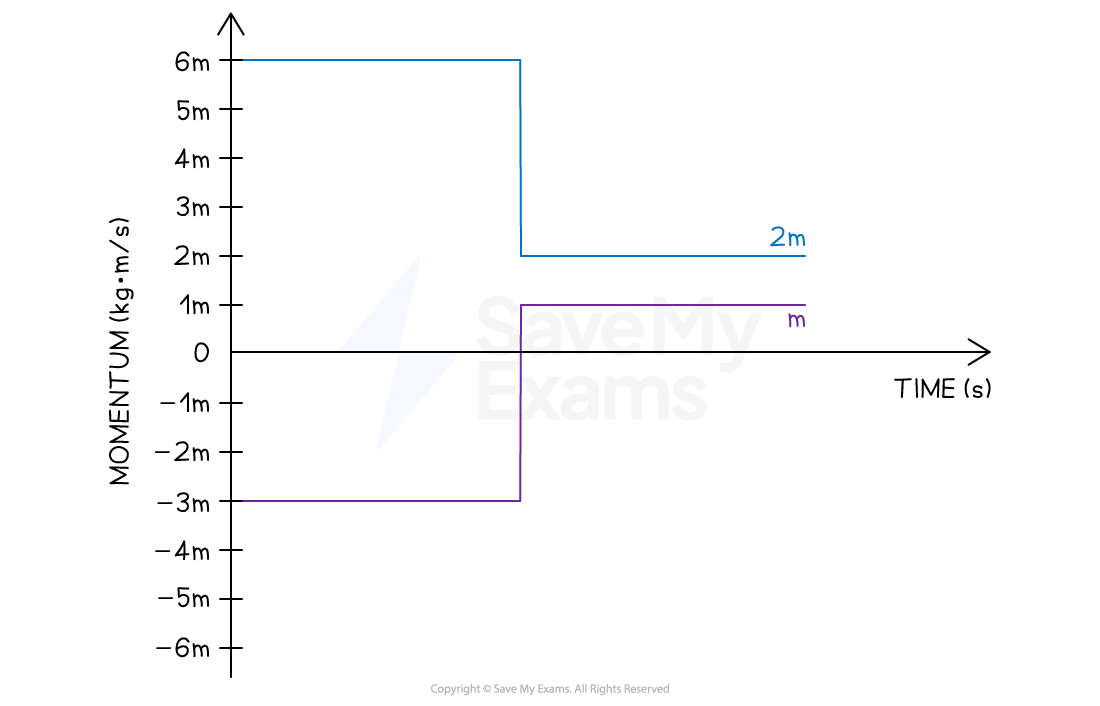
Graph showing momentum (kg·m/s) on the y-axis and time (s) on the x-axis. The blue line represents the trolley of mass 2m, and the purple line represents the trolley of mass m. The 2m trolley has a momentum of +6m before and a momentum of +2m after. The m trolley has a momentum of -3m before and a momentum of +m after. The vertical lines represent change in momentum and is equal for both trolleys.

Therefore, option B is correct

Worked Example

A person of mass $68 kg$ holds a $5 kg$ box while riding a skateboard of mass $2 kg$ toward the west at a speed of $2.0 m / s$ . The person throws the box to the east, giving it a speed of $5.0 m / s$ .

What is the person's final velocity after throwing the box?

Answer:

Step 1: Analyze the scenario

Initially, the system (the person, skateboard, and box) moves to the west with the same speed
Before the person throws the box, the system has:
- a combined mass of $(68 + 2 + 5) = 75 kg$
- an initial velocity of $v_{0} = + 2.0 m / s$ (we can define this as the positive direction)
After the person throws the box to the east:
- the person and the skateboard (total mass = $70 kg$ ) continue to move west (positive direction) with final velocity $v$
- the box $(m_{b o x} = 5 kg)$ has a velocity of $v_{b o x} = - 5.0 m / s$ (negative direction)

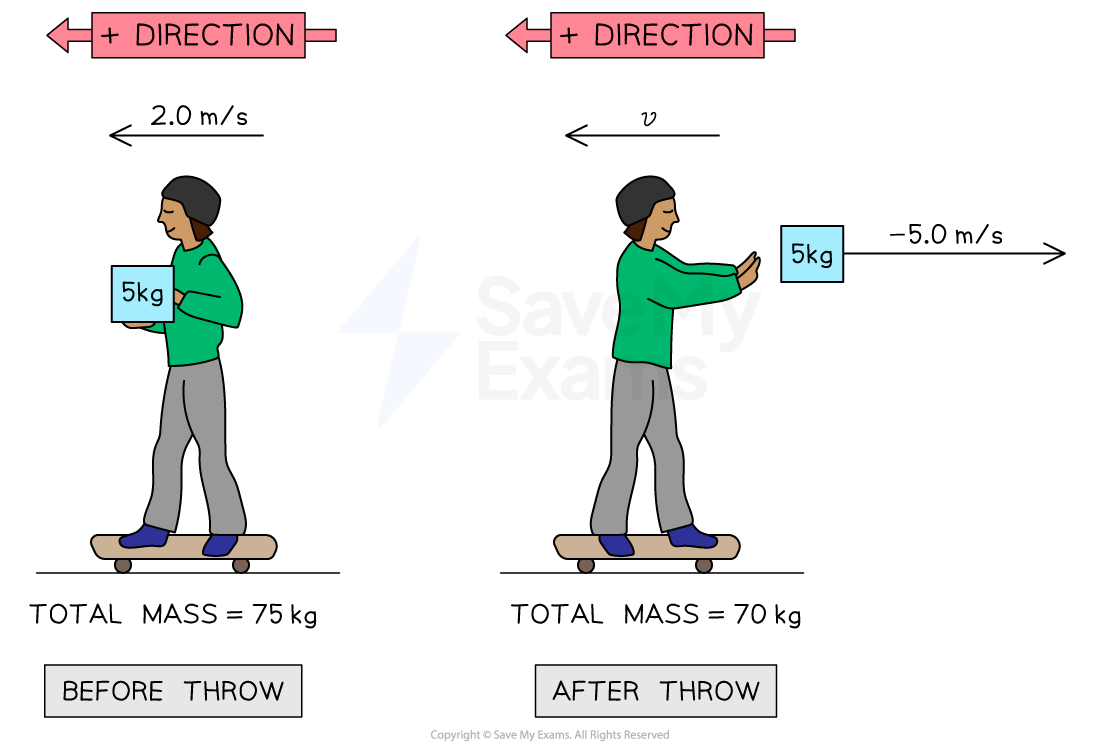
A person on a skateboard holds a 5 kg box and travels to the left at 2.0 m/s. In the second image, they throw the 5 kg box to the right at 5.0 m/s, reducing their mass from 75 kg to 70 kg and increasing their velocity to v.

Step 2: Apply the principle of conservation of momentum

Conservation of momentum: the total momentum before the throw = the total momentum after the throw

$\sum {\vec{p}}_{i} = \sum {\vec{p}}_{f}$

$(m_{p e r s o n} + m_{s k a t e b o a r d} + m_{b o x}) v_{0} = (m_{p e r s o n} + m_{s k a t e b o a r d}) v + m_{b o x} v_{b o x}$

$(75) (2.0) = 70 v + (5) (- 5.0)$

$150 = 70 v - 25$

Therefore, the final velocity of the person is

$v = \frac{150 + 25}{70} = 2.5 m / s$

Examiner Tips and Tricks

Using representations to analyze physical situations is a crucial skill in AP Physics 1. Furthermore, drawing momentum graphs or charts can be particularly useful for solving momentum conservation problems which involve determining the final states of objects involved in collisions.

Impulse & total momentum

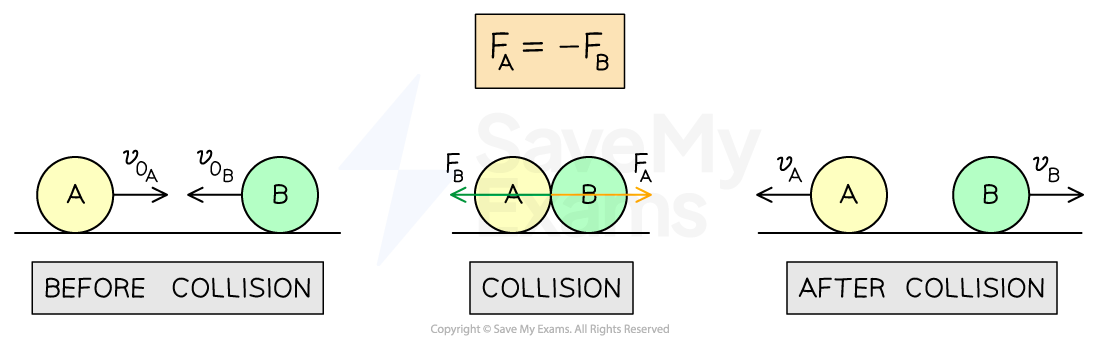
Conservation of momentum is a direct result of Newton's third law, which states:

The impulse exerted by object A on object B is equal and opposite to the impulse exerted by object B on object A

If the total momentum of a system changes, that change is equivalent to the impulse exerted on the system

$\vec{J} = ∆ \vec{p}$

Where:
- $\vec{J}$ = impulse exerted on the system, in $N \cdot s$
- $∆ \vec{p}$ = change in momentum of the system, in $kg \cdot m / s$
When two objects, A and B, collide:
- object A exerts a force on object B of magnitude $F_{A}$
- object B exerts a force on object A of magnitude $F_{B}$
- the forces are equal in magnitude and opposite in direction $F_{A} = - F_{B}$
- the forces, and therefore impulses, act for the amount of time the objects are in contact
This results in an alternative form of the principle of conservation of momentum which states:

The change in momentum of object A is equal and opposite to the change in momentum of object B

Mathematically, this can be written as:

$∆ {\vec{p}}_{A} = - ∆ {\vec{p}}_{B}$

Where:
- $∆ {\vec{p}}_{A}$ = change in momentum of object A, in $kg \cdot m / s$
- $∆ {\vec{p}}_{B}$ = change in momentum of object B, in $kg \cdot m / s$

Third law force pair during a collision

A collision between two balls, A and B. "Before collision" shows A and B moving toward each other with velocities v0A and v0B respectively. "Collision" shows forces FA and FB acting which are equal in magnitude and opposite in direction. "After collision" shows A and B moving apart with velocities vA and vB respectively. — **According to Newton's third law, the force exerted by A on B is equal to the force exerted by B on A and opposite in direction. The same is true for the impulse exerted by each sphere.**

Worked Example

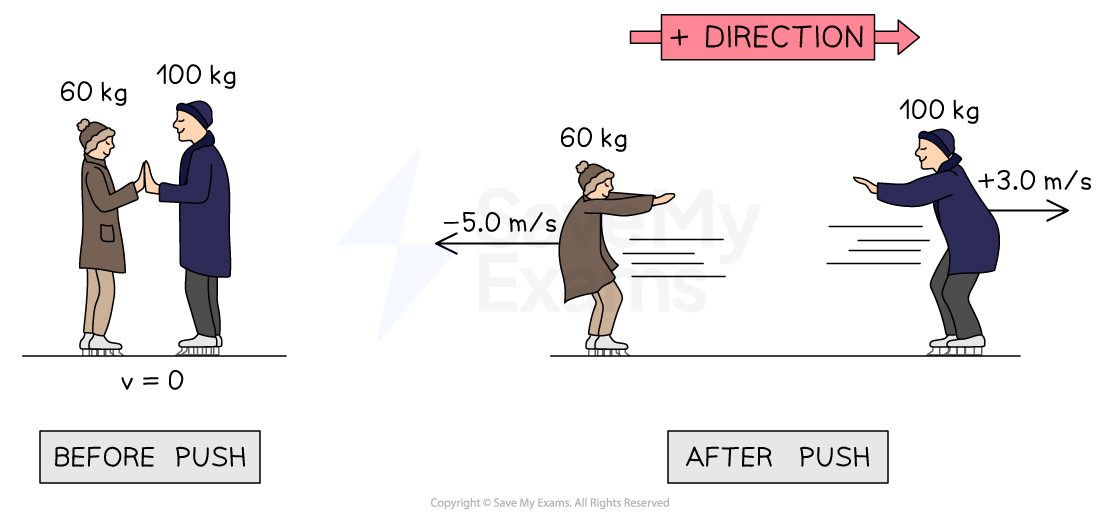
Two ice skaters of mass $60 kg$ and $100 kg$ are initially stationary on a frictionless, horizontal ice surface. They push against each other simultaneously with a force of magnitude $150 N$ for $2.0 s$ . One of the skaters moves to the left at a velocity of $5.0 m / s$ and the other skater moves to the right at a velocity of $v$ .

(A) Determine which skater has a final velocity of $5.0 m / s$ .

(B) Calculate the final velocity of the other skater.

Answer:

Part (A)

Step 1: Analyze the scenario

Initially, the two skaters are at rest, so the initial momentum is zero
When they push against each other, the impulse they exert on one another is equal and opposite and causes a change in momentum

Step 2: Determine the change in momentum

The impulse exerted by the skaters is equal to the change in momentum

$\vec{J} = ∆ \vec{p} = {\vec{F}}_{a v g} ∆ t$

The average force exerted by each skater is $F_{a v g} = 150 N$ for a period of $∆ t = 2.0 s$ , so the change in momentum is

$∆ p = 150 \times 2.0 = 300 kg \cdot m / s$

Step 3: Determine the mass of the skater with a final velocity of 5.0 m/s

Since the initial velocity of each skater is zero, the change in momentum is equal to the product of their mass and final velocity

$∆ \vec{p} = m ∆ \vec{v} = m \vec{v}$

The mass of the skater with a final velocity of $5.0 m / s$ is:

$m = \frac{∆ p}{v} = \frac{300}{5.0} = 60 kg$

Part (B)

Step 1: Analyze the scenario

After the push, the skaters move away from each other, so one of the velocities will be negative
The $60 kg$ skater moves to the left at a speed of $5.0 m / s$
Therefore, the $100 kg$ skater moves to the right at a speed of $v$
We can define the direction of the $100 kg$ skater as the positive direction

Step 2: Apply the principle of conservation of momentum

Conservation of momentum: the total momentum before the push is equal to the total momentum after

$\sum {\vec{p}}_{i} = \sum {\vec{p}}_{f}$

$0 = 100 v - 300$

$100 v = 300$

Therefore, the final velocity of the $100 kg$ skater is:

$v = \frac{300}{100} = 3.0 m / s$

Part (C)

Step 1: Analyze the scenario

After the push:
- the $100 kg$ skater moves to the right (positive direction) at a velocity of $+ 3.0 m / s$
- the $60 kg$ skater moves to the left (negative direction) at a velocity of $- 5.0 m / s$

Step 2: Deduce the initial positions of the skaters

Before the push:
- the $100 kg$ skater is to the right of the $60 kg$ skater
- the $60 kg$ skater is to the left of the $100 kg$ skater

Two people of mass 60 kg (left) and 100 kg (right) pushing each other on ice skates. Before push: both stationary, so v = 0. After push: moving apart, 60 kg at -5.0 m/s, 100 kg at +3.0 m/s.

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Impulse GraphsNext:Momentum of a System

The Principle of Conservation of Momentum (College Board AP® Physics 1: Algebra-Based) : Study Guide

The principle of conservation of linear momentum

Example 1: two identical objects colliding

Conservation of momentum between identical spheres

Example 2: two objects rebounding

Conservation of momentum between non-identical spheres

Impulse & total momentum

Third law force pair during a collision

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Unit 1: Kinematics

Scalars & Vectors

Scalar & Vector Quantities

Combining Vectors

Displacement, Velocity & Acceleration

Displacement

Velocity

Acceleration

Representing Motion

Kinematic Equations

Motion Graphs

Reference Frames & Relative Motion

Vectors & Motion

Vectors & Motion in Two Dimensions

Projectile Motion

Unit 2: Force & Translational Dynamics

Systems & Center of Mass

Describing Systems

Center of Mass

Forces & Free-Body Diagrams

Free Body Diagrams

Forces as Interactions

Net Force

Translational Equilibrium

Newton's Laws

Newton's First Law

Newton's Second Law

Newton's Third Law

Tension

Tension

Tension in Ideal & Non-Ideal Strings

Gravitational Force

Newton's Law of Gravitation

Gravitational Force

Gravitational Field

Acceleration Due to Gravity

Gravitational Field Strength Equation

Weight

Apparent Weight

Inertial vs Gravitational Mass

Kinetic & Static Friction

Kinetic Friction

Kinetic Friction Force Equation

Static Friction

Static Friction Force Formula

Slipping & Sliding

Spring Forces

Hooke's Law

Circular Motion

Uniform Circular Motion

Acceleration in Circular Motion

Circular Motion in a Vertical Loop

Circular Motion Examples

Kepler's Third Law

Unit 3: Work, Energy & Power

Work

Defining Work & Work Done

Calculating Work Done

Translational Kinetic Energy & Potential Energy

Translational Kinetic Energy

Potential Energy

Elastic Potential Energy

Gravitational Potential Energy Near a Surface

Gravitational Potential Energy Between Objects

Work-Energy Theorem

Work-Energy Theorem

Conservation of Energy

Conservation of Energy

Power