Momentum of a System (College Board AP® Physics 1: Algebra-Based)

Study Guide

Written by: Katie M

Calculating velocity of a system's center of mass

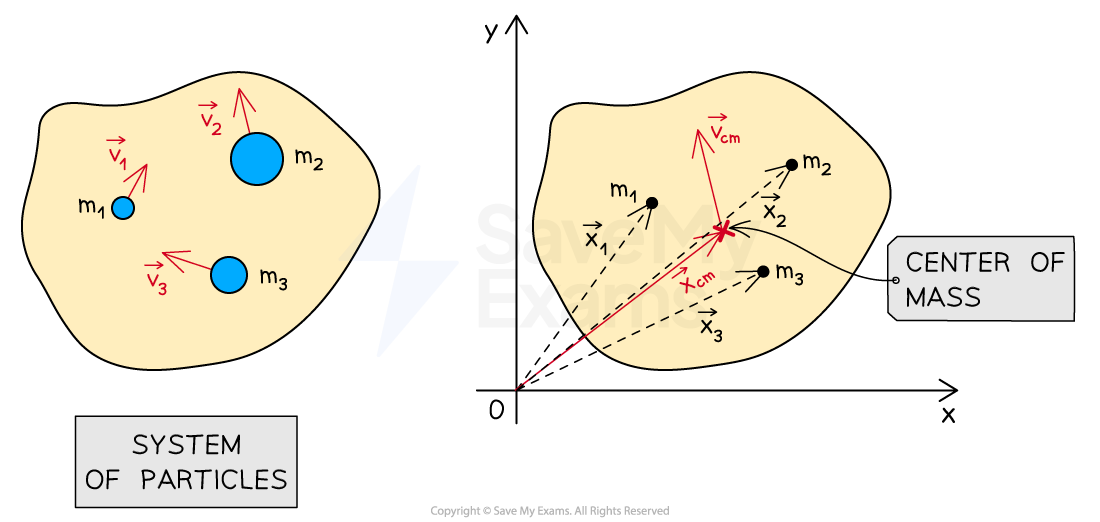
For a system of multiple objects, it can be useful to consider them as point particles with a common center of mass
Consider a system of three objects, each with individual masses and velocities
The position of the system's center of mass can be determined using:

${\vec{x}}_{c m} = \frac{\sum_{i} (m_{i} {\vec{x}}_{i})}{\sum m_{i}} = \frac{m_{1} x_{1} + m_{2} x_{2} + m_{3} x_{3}}{m_{1} + m_{2} + m_{3}}$

Where:
- ${\vec{x}}_{c m}$ = position of the system's center of mass, in $m$
- $m_{i}$ = mass of each object, in $kg$
- ${\vec{x}}_{i}$ = position of each object, in $m$
Similarly, the velocity of the system's center of mass can be determined using:

${\vec{v}}_{c m} = \frac{\sum_{i} (m_{i} {\vec{v}}_{i})}{\sum m_{i}} = \frac{m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2} + m_{3} {\vec{v}}_{3}}{m_{1} + m_{2} + m_{3}}$

Where:
- ${\vec{v}}_{c m}$ = velocity of the system's center of mass, in $m / s$
- ${\vec{v}}_{i}$ = velocity of each object, in $m / s$

Velocity of the center of mass of a system of particles

A system of three particles with their masses and velocity vectors on the left, and their position vectors on an XY-coordinate plane on the right showing the center of mass and its velocity. — **The motion of a system of particles can be described in terms of the velocity of the center of mass of the system**

Total momentum of a system

The total momentum of a system is equal to the sum of the momenta of the system’s constituent parts

$\vec{p} = \sum_{i} {\vec{p}}_{i} = \sum_{i} (m_{i} {\vec{v}}_{i})$

Consider a system of $n$ objects:

$\vec{p} = \sum_{i} {\vec{p}}_{i} = {\vec{p}}_{1} + {\vec{p}}_{2} + {\vec{p}}_{3} + . . . + {\vec{p}}_{n}$

$\vec{p} = \sum_{i} (m_{i} {\vec{v}}_{i}) = m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2} + m_{3} {\vec{v}}_{3} + . . . + m_{n} {\vec{v}}_{n}$

Therefore, a collection of objects with individual momenta can be described as one system with one center-of-mass velocity:

${\vec{v}}_{c m} = \frac{\sum_{i} {\vec{p}}_{i}}{\sum m_{i}} = \frac{\sum_{i} (m_{i} {\vec{v}}_{i})}{\sum m_{i}}$

We can also re-write the expression for the total momentum of the system as:

$\vec{p} = M {\vec{v}}_{c m}$

Where:
- $\vec{p}$ = total momentum of the system, in $kg \cdot m / s$
- $M$ = total mass of the system, in $kg$
- ${\vec{v}}_{c m}$ = velocity of the center of mass of the system, in $m / s$

Worked Example

A rocket of mass $M$ and shuttle of mass $5 M$ are initially traveling together to the right with velocity $v$ , as shown in the diagram.

A shuttle connected to a rocket with a velocity v pointing to the right. The shuttle is rectangular, and the rocket is triangular.

The shuttle separates from the rocket and continues to travel to the right with velocity $v_{s}$ while the rocket continues to travel to the right with velocity $v_{r}$ , where $v_{r} > v$ , as shown in the following diagram.

A shuttle with a velocity vs separates from a rocket with velocity vr. Both arrows point to the right, the arrow labeled 'vr' is longer than the arrow labeled 'vs'.

Which of the following is true for the velocity $v_{c m}$ of the center of mass of the system after the shuttle and rocket separate?

A $v_{c m} = v_{s}$

B $v_{c m} = v$

C $v_{c m} < v$

D $v < v_{c m} < v_{r}$

The correct answer is B

Answer:

Step 1: Analyze the scenario

When traveling together, the velocity of the center of mass of the rocket and shuttle is

$v_{c m} = \frac{\sum_{i} (m_{i} {\vec{v}}_{i})}{\sum m_{i}} = \frac{(M + 5 M) v}{(M + 5 M)}$

$v_{c m} = v$

During the separation, no external forces act on the system, so there is no impulse on the system

Step 2: Eliminate incorrect options

Since no external forces act on the system, the total momentum of the system must be constant

$\vec{p} = (M + 5 M) {\vec{v}}_{c m}$

The velocity of the center of mass was $v$ before the separation
Therefore, it cannot be greater than $v$ after the separation
- This eliminates option D
It also cannot be less than $v$ after the separation
- This eliminates option C
After the separation, the velocity of the rocket $v_{r}$ was greater than $v$
Therefore, the velocity of the shuttle $v_{s}$ must be less than $v$
- This eliminates option A

Step 3: Deduce the correct option

As the center of mass was moving with velocity $v$ before the separation, it will continue to move with velocity $v$
- Therefore, option B is correct

Worked Example

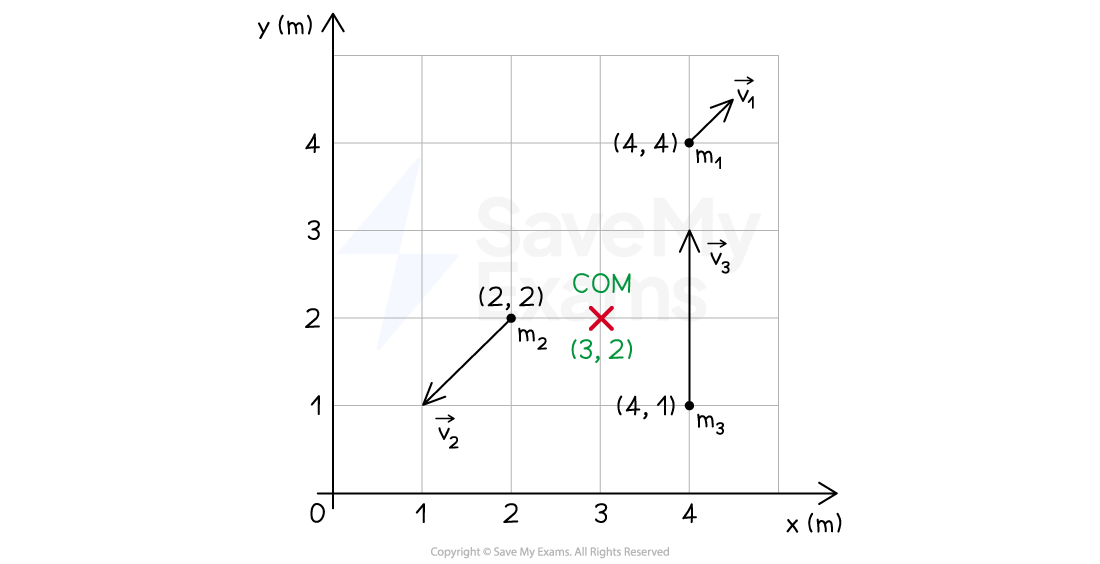
The masses and velocities of three objects in a system are given in the table below.

Particle	Mass (kg)	Velocity (m/s)
1	1	1
2	3	2
3	2	3

The positions of the three objects in an xy plane are shown in the diagram.

XY-coordinate graph showing three points labeled m1 at (4,4), m2 at (2, 2), and m3 at (4,1), with vectors v1, v2, and v3 indicating directions from each point. X and Y axes are labeled in meters (m).

For the system of three objects, determine:

(A) the position of the center of mass, ${\vec{x}}_{c m}$ .

(B) the velocity of the center of mass, ${\vec{v}}_{c m}$ .

Answer:

Part (A)

Step 1: Determine the xy coordinates of the positions of each object

Graph showing points (2,2), (4,4), and (4,1). Points are labeled as m2, m1, and m3 respectively. Arrows indicate velocities v1, v2, and v3

Object 1 $(m_{1} = 1 kg)$ has coordinates $(4, 4)$ , so $x_{1} = 4 m$ and $y_{1} = 4 m$
Object 2 $(m_{2} = 3 kg)$ has coordinates $(2, 2)$ , so $x_{2} = 2 m$ and $y_{2} = 2 m$
Object 3 $(m_{3} = 2 kg)$ has coordinates $(4, 1)$ , so $x_{3} = 4 m$ and $y_{3} = 1 m$

Step 2: Determine the x-component of the position of the center of mass

$x_{c m} = \frac{m_{1} x_{1} + m_{2} x_{2} + m_{3} x_{3}}{m_{1} + m_{2} + m_{3}}$

$x_{c m} = \frac{(1 \times 4) + (3 \times 2) + (2 \times 4)}{1 + 3 + 2} = 3 m$

Step 3: Determine the y-component of the position of the center of mass

$y_{c m} = \frac{m_{1} y_{1} + m_{2} y_{2} + m_{3} y_{3}}{m_{1} + m_{2} + m_{3}}$

$y_{c m} = \frac{(1 \times 4) + (3 \times 2) + (2 \times 1)}{1 + 3 + 2} = 2 m$

Step 4: Determine the position of the center of mass

The xy coordinate of the position of the center of mass is ${\vec{x}}_{c m} = (3, 2)$

Graph showing three masses (m1, m2, m3) at points (4,4), (2,2), (4,1), respectively, with vectors v1, v2, v3 and their center of mass (COM) at (3,2).

Part (B)

Step 1: Determine the xy velocity components of each object

The velocity vectors of $m_{1}$ and $m_{2}$ are in opposite directions
Using their position coordinates, we can determine the angle between their velocity vectors and the x-axis
This angle can be found using $\tan θ = \frac{y}{x}$
The positions of $m_{1}$ and $m_{2}$ are $(4, 4)$ and $(2, 2)$ respectively, therefore:
- $\tan θ = \frac{2}{2} = \frac{4}{4} = 1$
- $θ = \tan^{- 1} (1) = 45 °$

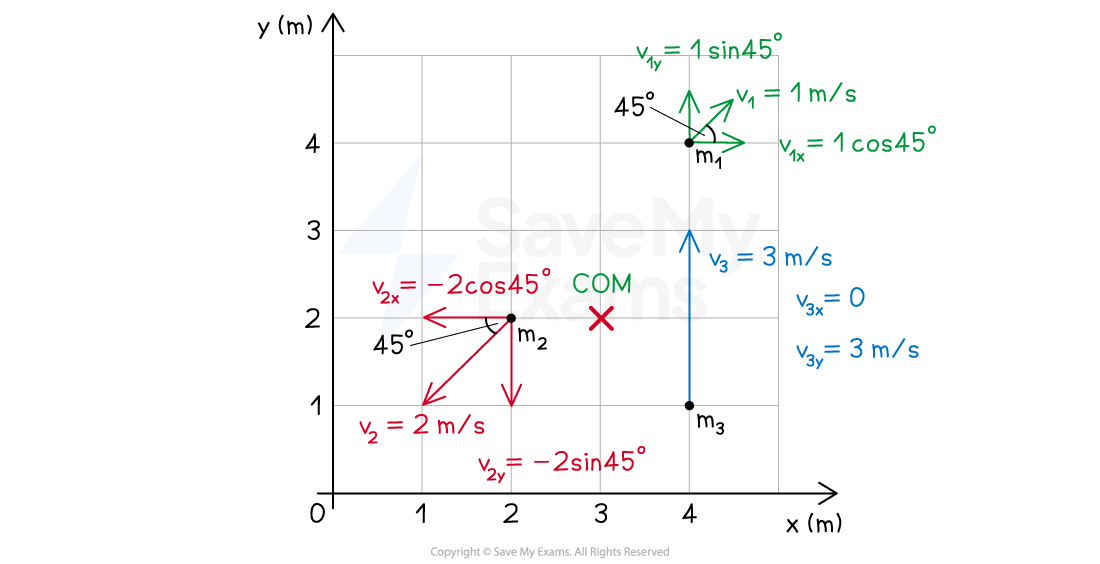
A labeled graph showing three masses (m1, m2, m3) with their velocities (v1, v2, v3) at coordinates, arrow vectors indicating direction and magnitude, and a center of mass labeled "COM".

The x- and y- velocity components of object 1 $(m_{1} = 1 kg)$ are:
- $v_{1 x} = 1 \cos 45 °$
- $v_{1 y} = 1 \sin 45 °$
The x- and y- velocity components of object 2 $(m_{2} = 3 kg)$ are:
- $v_{2 x} = - 2 \cos 45 °$
- $v_{2 y} = - 2 \sin 45 °$
The x- and y- velocity components of object 3 $(m_{3} = 2 kg)$ are:
- $v_{3 x} = 0$
- $v_{3 y} = 3$

Step 2: Determine the x-component of the velocity of the center of mass

$v_{x, c m} = \frac{m_{1} v_{x 1} + m_{2} v_{x 2} + m_{3} v_{x 3}}{m_{1} + m_{2} + m_{3}}$

$v_{x, c m} = \frac{(1 \times 1 \cos 45 °) - (3 \times 2 \cos 45 °) + 0}{1 + 3 + 2} = - 0.589$

Step 3: Determine the y-component of the velocity of the center of mass

$v_{y, c m} = \frac{m_{1} v_{y 1} + m_{2} v_{y 2} + m_{3} v_{y 3}}{m_{1} + m_{2} + m_{3}}$

$v_{y, c m} = \frac{(1 \times 1 \sin 45 °) - (3 \times 2 \sin 45 °) + (2 \times 3)}{1 + 3 + 2} = 0.411$

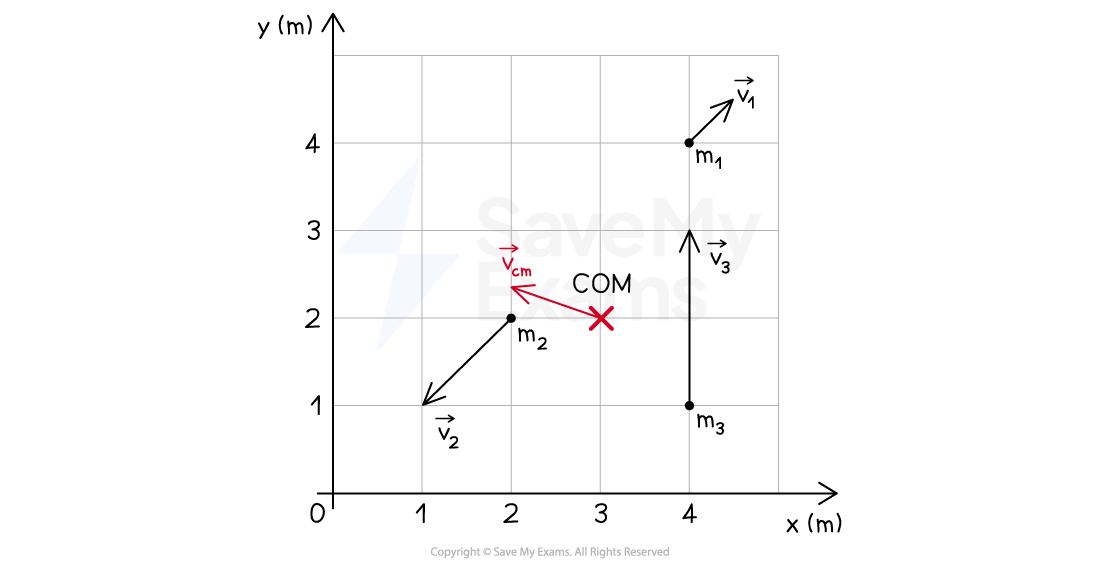
Step 4: Determine the velocity of the center of mass

Using Pythagoras theorem, the magnitude of the velocity is:

${\vec{v}}_{c m} = \sqrt{{(v_{x, c m})}^{2} + {(v_{y, c m})}^{2}}$

${\vec{v}}_{c m} = \sqrt{0 . 589^{2} + 0 . 411^{2}} = 0.72 m / s$

Using trigonometry, the direction of the velocity is:

$θ_{c m} = \tan^{- 1} (\frac{v_{y, c m}}{v_{x, c m}})$

$θ_{c m} = \tan^{- 1} (- \frac{0.411}{0.589}) = - 35 °$

The magnitude and direction of the velocity of the system's center of mass can be represented on the xy plane as:

Graph showing points m1, m2, and m3 with respective velocities v1, v2, and v3. An X at the center labeled COM indicates the center of mass with a velocity vector vcm in red.

Examiner Tips and Tricks

Make sure you understand the position and velocity of a center of mass:

is not necessarily at the geometric center of a system
does not change regardless of what the objects in a system do

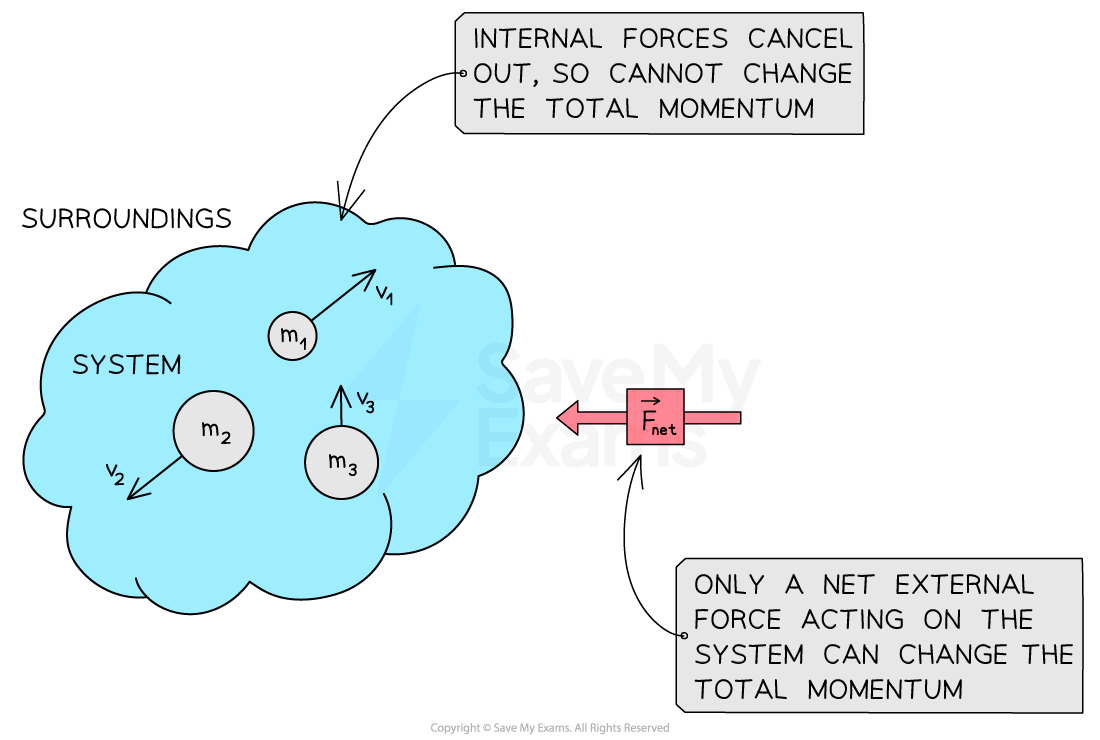
Conditions for the transfer of momentum

A system may be selected so that the total momentum of that system is constant
- The system can be defined as the objects involved in the interaction
- The surroundings can then be defined as anything outside of the chosen system

The total momentum of a system can be changed only by a net external force
When the net external force is nonzero:
- any change to the momentum of a system is due to a transfer of momentum between the system and its surroundings
- the conservation of momentum principle is not valid
When the net external force is zero (i.e. in an isolated system):
- the total momentum of the system is constant
- the velocity of the system’s center of mass is constant
- any change to the momentum of an object within the system must be balanced by an equal and opposite change of momentum elsewhere within the system
- the conservation of momentum principle is valid

Transfer of momentum by a net external force

A system with three masses (m1, m2, m3) moving in different directions within a surrounding. One label explains that the internal forces cancel out, so these cannot change the total momentum. The other label explains that only a net external force can change the total momentum. — **If the net external force on the selected system is nonzero, momentum is transferred between the system and the surroundings**

Worked Example

A dart of mass $m$ moving horizontally with constant speed becomes embedded in a block of mass $M$ , as shown in the diagram. The dart and block move together with speed $v$ immediately after the collision. The block is suspended from two light strings and swings up to a maximum height $h$ above the block’s initial position.

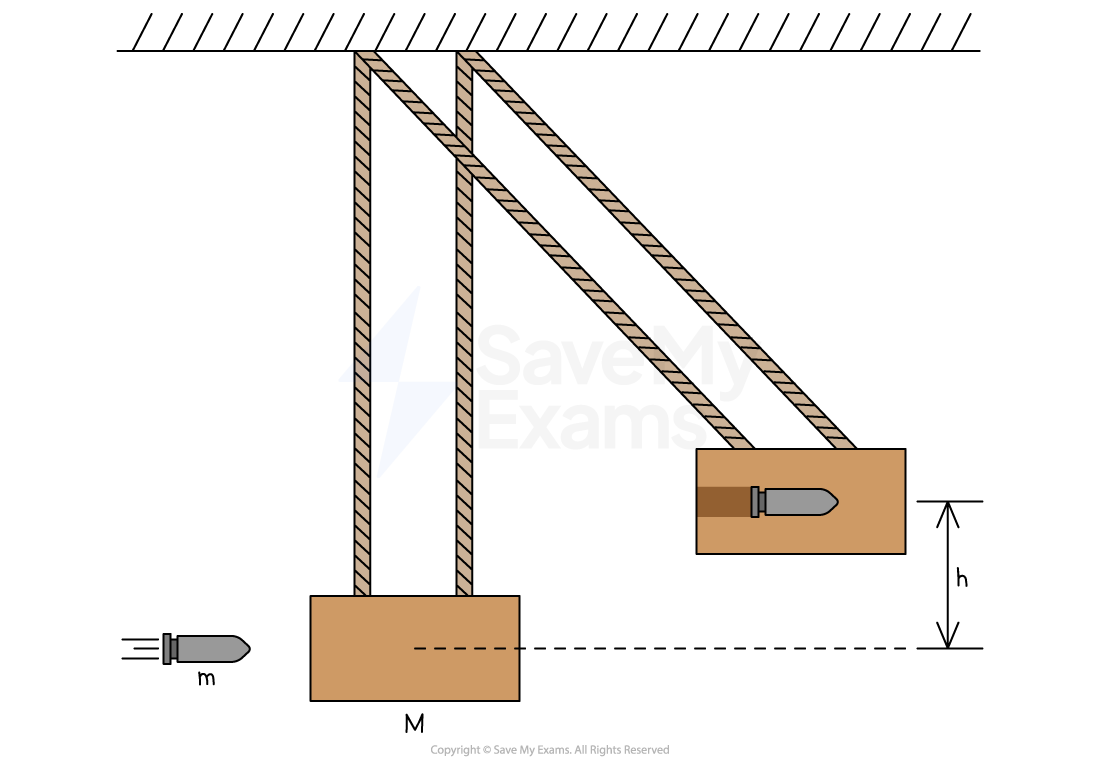
A dart with mass m moves towards a wooden block of mass M suspended by two light strings, causing the block to swing and rise to height h after impact.

In which of the following systems is linear momentum conserved?

A The dart-block system in the horizontal direction

B The dart-block-string system

C The dart-block-Earth system

D The dart-block-string-Earth system

The correct answer is A

Answer:

Step 1: Analyze the scenario

This scenario, known as the Ballistic Pendulum, can be analyzed in three stages
- Stage 1: before the collision
- Stage 2: after the collision
- Stage 3: at the maximum height
According to the Impulse-Momentum Theorem, external forces cause an impulse to act which results in a change in momentum
Therefore, linear momentum will only be conserved in a system where there are no external forces acting

Step 2: Eliminate incorrect options

The Earth exerts an external (gravitational) force when there is a change in height, so conservation of momentum cannot be used
- This eliminates options C and D
The strings are described as light, so they can be ignored in calculations of momentum
- This eliminates option B

Step 3: Deduce the correct option

Before the collision, the dart is moving horizontally, and just after the collision, the dart and the block continue to move horizontally momentarily
Therefore, the conservation of momentum principle can be applied to the dart-block system in the horizontal direction only
- Therefore, option A is correct

Examiner Tips and Tricks

You must not perform conservation of momentum calculations when the net external force on a system is nonzero, as the conservation of momentum principle is not valid in this situation. However, you will be expected to select systems appropriately so that the net external force on the system is zero. Often in AP Physics 1, the system will be chosen for you, so you must read the question carefully and analyze the system you are given.

Last updated: 21 December 2024

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:The Principle of Conservation of MomentumNext:Momentum in Collisions

Momentum of a System (College Board AP® Physics 1: Algebra-Based)

Study Guide

Calculating velocity of a system's center of mass

Velocity of the center of mass of a system of particles

Total momentum of a system

Conditions for the transfer of momentum

Transfer of momentum by a net external force

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Unit 1: Kinematics

Scalars & Vectors

Scalar & Vector Quantities

Combining Vectors

Displacement, Velocity & Acceleration

Displacement

Velocity

Acceleration

Representing Motion

Kinematic Equations

Motion Graphs

Reference Frames & Relative Motion

Vectors & Motion

Vectors & Motion in Two Dimensions

Projectile Motion

Unit 2: Force & Translational Dynamics

Systems & Center of Mass

Describing Systems

Center of Mass

Forces & Free-Body Diagrams

Free Body Diagrams

Forces as Interactions

Net Force

Translational Equilibrium

Newton's Laws

Newton's First Law

Newton's Second Law

Newton's Third Law

Tension

Tension

Tension in Ideal & Non-Ideal Strings

Gravitational Force

Newton's Law of Gravitation

Gravitational Force

Gravitational Field

Acceleration Due to Gravity

Gravitational Field Strength Equation

Weight

Apparent Weight

Inertial vs Gravitational Mass

Kinetic & Static Friction

Kinetic Friction

Kinetic Friction Force Equation

Static Friction

Static Friction Force Formula

Slipping & Sliding

Spring Forces

Hooke's Law

Circular Motion

Uniform Circular Motion

Acceleration in Circular Motion

Circular Motion in a Vertical Loop

Circular Motion Examples

Kepler's Third Law

Unit 3: Work, Energy & Power

Work

Defining Work & Work Done

Calculating Work Done

Translational Kinetic Energy & Potential Energy

Translational Kinetic Energy

Potential Energy

Elastic Potential Energy

Gravitational Potential Energy Near a Surface

Gravitational Potential Energy Between Objects

Work-Energy Theorem

Work-Energy Theorem

Conservation of Energy

Conservation of Energy

Power

Calculating Power