Study GuidesExam QuestionsPast Papers
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 4: Linear MomentumConservation of Linear MomentumMomentum in Explosions

Momentum in Explosions (College Board AP® Physics 1: Algebra-Based)

Study Guide

Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Momentum in explosions

  • The conservation of momentum principle can be used to analyze explosions

  • An explosion is defined as

An interaction in which forces internal to the system move objects within that system apart

  • Some examples of explosions include:

    • the recoil of a gun after shooting a bullet

    • the radioactive emission of a particle from an unstable nucleus

Explosions in one dimension

  • Explosions in one dimension (1D) usually involve one stationary object becoming two objects that move away from each other along the same line

    • Before the explosion, the velocity, and therefore momentum, is zero

    • After the collision, the velocity vectors are directed along the same axis and can be either positive or negative

  • When solving problems involving explosions in one dimension:

    • identify the objects included in the system, making sure there are no net external forces

    • write an expression for the momentum of each object after the explosion

    • write an expression for the total momentum of the system before and after the explosion

    • apply the conservation of momentum principle

    • solve for the unknown quantity

An explosion in one dimension where a single object AB becomes two objects A and B moving along the same line in opposite directions. Before the explosion, object AB is at rest. After the explosion, A and B move away from each other with velocities vA, and vB respectively.
During an explosion in one dimension, an internal force causes a single object, AB, to become two objects, A and B, which move along the same line in opposite directions

  • Applying the conservation of momentum principle (defining the positive direction to the right):

0 space equals space m subscript B v with rightwards arrow on top subscript B space minus space m subscript A v with rightwards arrow on top subscript A

  • Since the velocity of each object is directed along the same axis, the vector notation can be removed

m subscript A over m subscript B space equals space v subscript B over v subscript A

Explosions in two dimensions

  • Explosions in two dimensions (2D) usually involve one stationary object becoming two or more objects that move away from each other in different directions

    • Before the explosion, the velocity, and therefore momentum, is zero

    • After the explosion, the velocity vectors may have both horizontal and vertical components

  • When solving problems involving explosions in two dimensions:

    • identify the objects included in the system, making sure there are no net external forces

    • write expressions for the x- and y- components of the momentum of each object after the explosion

    • write expressions for the total momentum of the system in each direction before and after the explosion

    • apply the conservation of momentum principle to each direction separately

    • solve for the unknown quantity using Pythagoras' theorem

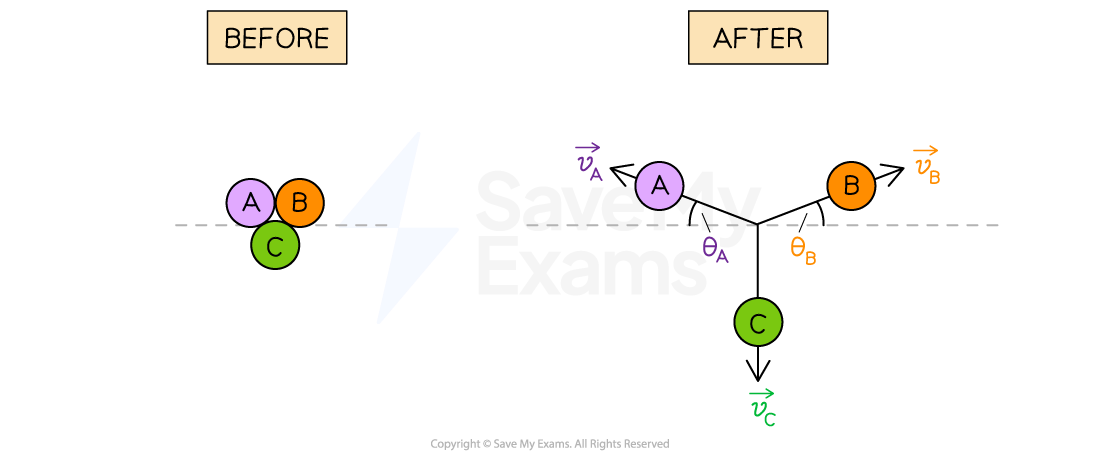
An explosion in two dimensions where single object ABC becomes three objects A, B and C which move apart in different directions. Before the explosion, object ABC is at rest. After the explosion, object A moves to the left at an angle θA above the horizontal with velocity vA, object B moves to the right at an angle θB above the horizontal with velocity vB, and object C moves vertically down with velocity vC.
After an explosion of object ABC in two dimensions, three objects, A, B, and C, move off in different directions

  • If no external forces act on a system, horizontal and vertical components of momentum are conserved

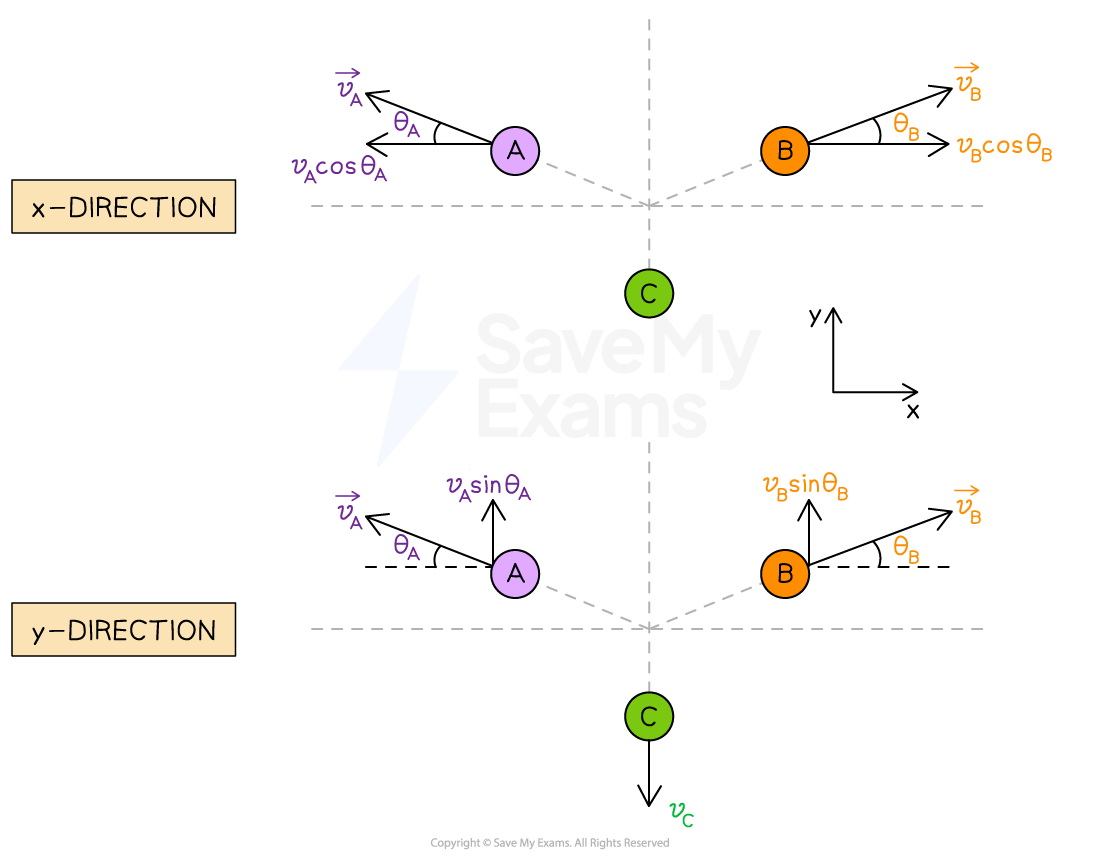
  • Applying the conservation of momentum principle:

0 space equals space m subscript A v with rightwards arrow on top subscript A space plus space m subscript B v with rightwards arrow on top subscript B space plus space m subscript C v with rightwards arrow on top subscript C

  • The components of the velocities in the x-direction are:

0 space equals space space m subscript B v subscript B space cos space theta subscript B space minus space m subscript A v subscript A space cos space theta subscript A

  • The components of the velocities in the y-direction are:

0 space equals space m subscript A v subscript A space sin space theta subscript A space plus space m subscript B v subscript B space sin space theta subscript B space minus space m subscript C v subscript C

For an explosion in two dimensions where a single object ABC becomes three objects A, B and C, the velocities must be resolved into x- and y- components. Object A moves to the left at an angle θA above the horizontal with velocity vA, so it has a velocity of vAcosθA in the x-direction and vAsinθA in the y-direction. Object B moves to the right at an angle θB above the horizontal with velocity vB, so it has a velocity of vBcosθB in the x-direction and vBsinθB in the y-direction. Object C moves vertically down with velocity vC, so it has a vertical velocity component only.
To solve problems involving explosions in two dimensions, the velocity vectors must be resolved into their horizontal and vertical components

Worked Example

A stationary uranium nucleus undergoes fission and splits into two fragments of unequal mass and two neutrons, where m subscript 1 space greater than space m subscript 2 space much greater-than space m subscript n, as shown in the diagram.

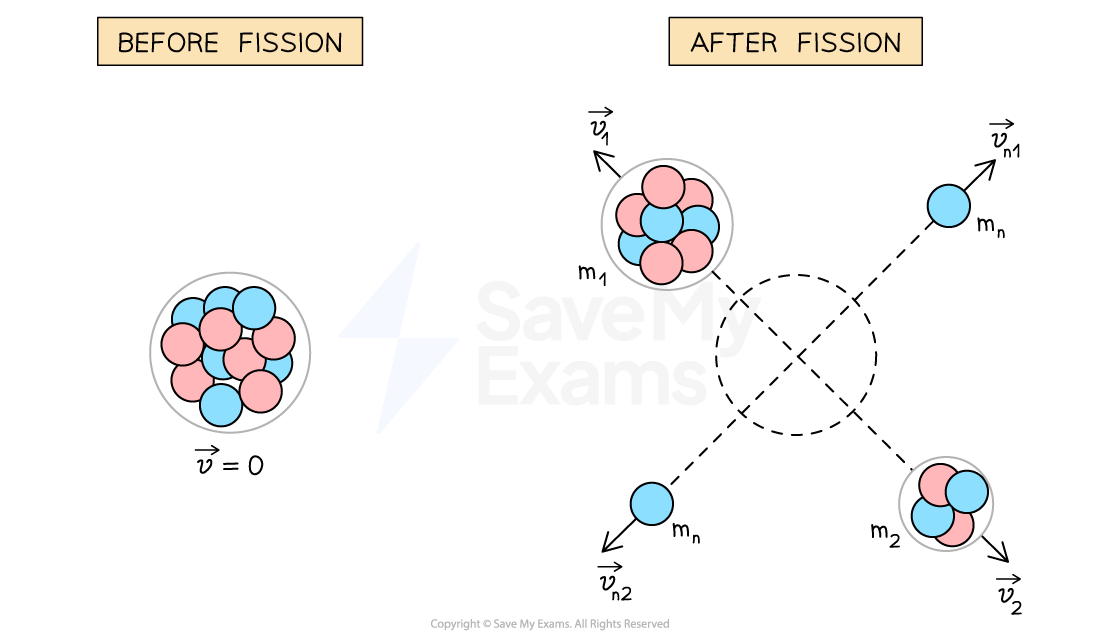
Fission of a uranium nucleus. Before fission, the uranium nucleus is stationary. After fission, a heavier nucleus of mass m1 moves with velocity v1 in the opposite direction to a lighter nucleus with mass m2 and velocity v2. At right angles to the nuclei, two neutrons of mass mn move in opposite directions with velocities vn1 and vn2 respectively

Which of the following is true for the velocities of the fragments?

A      v subscript 1 over v subscript 2 space greater than space 1

B      v subscript 1 over v subscript 2 space less than space 1

C      v subscript 2 space less than space v subscript n 1 end subscript space less than space v subscript n 2 end subscript

D      v subscript 1 space greater than space v subscript n 1 end subscript space equals space v subscript n 2 end subscript

The correct answer is B

Answer:

Step 1: Analyze the scenario

  • The uranium nucleus is initially at rest, so the total momentum before the fission is zero

  • The total momentum of the system must be conserved

  • So, the final total momentum of the four fragments must also be zero

  • The fragments move along the same line, and the neutrons move along the same line, so, the individual components of their momenta are equal in magnitude and opposite in direction

Step 2: Eliminate incorrect options

  • For momentum to be conserved

    • the heavier the fragment, the lower the velocity

    • the lighter the fragment, the greater the velocity

  • Applying conservation of momentum in the direction of the neutrons:

m subscript n v subscript n 1 end subscript space equals space minus m subscript n v subscript n 2 end subscript

v subscript n 1 end subscript space equals space minus v subscript n 2 end subscript

Deducing the component of the momenta in the direction of the neutrons. The positive direction is defined to the right. Neutrons have equal mass so they must have equal and opposite velocities.

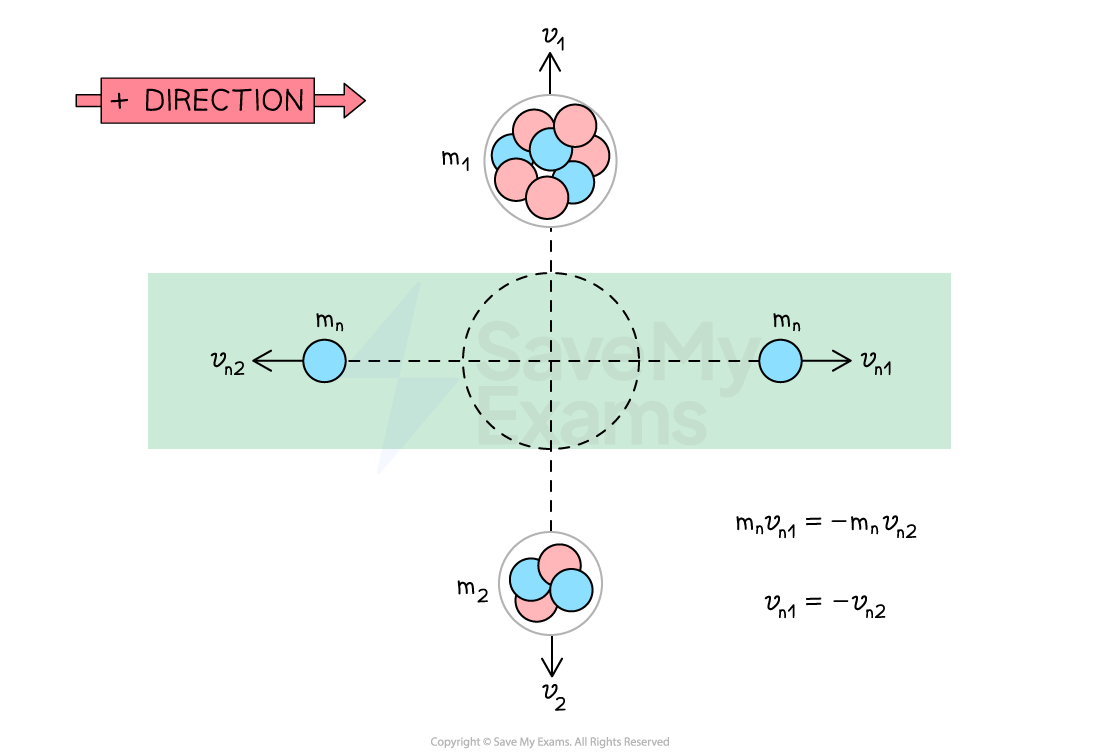
  • The neutrons have equal mass, hence, they must have equal velocities

    • This eliminates option C

  • The neutrons are much lighter than the two fragments, so they must have higher velocities

    • This eliminates option D

Step 3: Deduce the correct option

  • Applying conservation of momentum in the direction of the fragments:

m subscript 1 v subscript 1 space equals space minus m subscript 2 v subscript 2

v subscript 1 over v subscript 2 space equals space minus m subscript 2 over m subscript 1

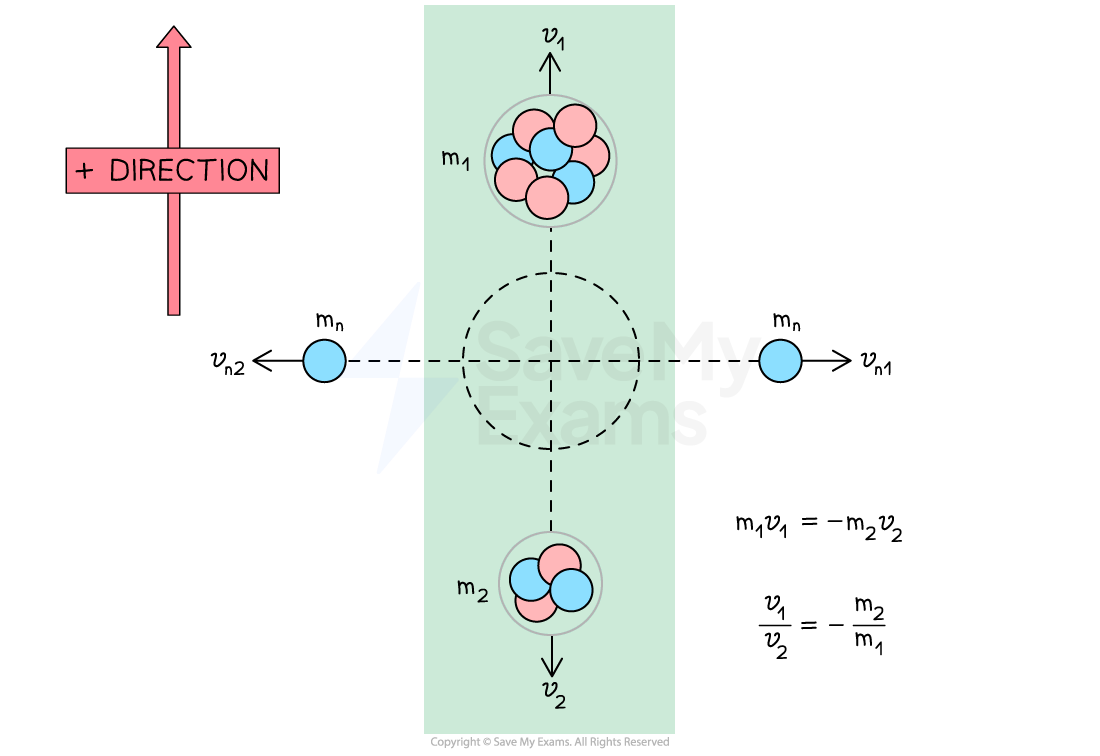
Deducing the component of the momenta in the direction of the fragments. The positive direction is defined upwards. The fragments have unequal masses so the heavier mass must have a smaller velocity.

  • Since m subscript 1 space greater than space m subscript 2, the ratio of the masses will be m subscript 2 over m subscript 1 space greater than space 1, therefore:

v subscript 1 over v subscript 2 space greater than space minus 1

  • Which is equivalent to:

v subscript 1 over v subscript 2 space less than space 1

  • Therefore, option B is correct

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Momentum in CollisionsNext:Elastic & Inelastic Collisions
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.