Momentum in Collisions (College Board AP® Physics 1: Algebra-Based)

Study Guide

Test yourself

Author

Katie M

Expertise

Physics

Momentum in collisions

The conservation of momentum principle can be used to analyze collisions
A collision is defined as

An event in which two or more moving objects come together and exert a force on each another

In a collision, it is assumed that
- the internal forces between objects are much larger than the net external force exerted on the system
- the time interval during which the momentum changes is very short

Collisions in one dimension

Collisions in one dimension (1D) usually involve two objects interacting on a single straight line
- This means the velocity vectors before and after the collision are directed along the same axis and can be either positive or negative
When solving problems involving collisions in one dimension:
- identify the objects included in the system, making sure there are no net external forces
- write expressions for the momentum of each object before and after the collision
- write expressions for the total momentum of the system before and after the collision
- apply the conservation of momentum principle
- solve for the unknown quantity

A collision in one dimension between two objects A and B along the same line. Before the collision, object A moves towards stationary object B with velocity v0A. After the collision, A and B move away from each other with velocities vA, and vB respectively. — **During a collision in one dimension between two objects, A and B, they move along the same line before and after the collision**

Applying the conservation of momentum principle (defining the positive direction to the right):

$m_{A} {\vec{v}}_{0 A} = m_{B} {\vec{v}}_{B} - m_{A} {\vec{v}}_{A}$

Since the velocity of each object is directed along the same axis, the vector notation can be removed:

$\frac{m_{A}}{m_{B}} = \frac{v_{B}}{v_{0 A} + v_{A}}$

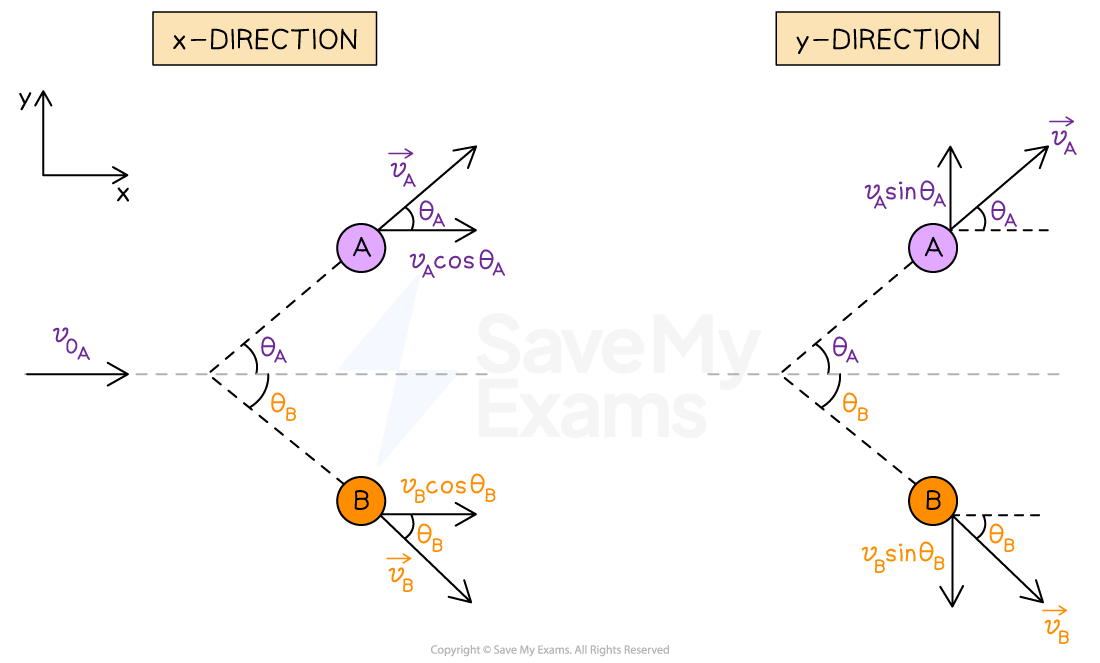
Collisions in two dimensions

Collisions in two dimensions (2D) usually involve an interaction between two objects in a plane
- This means the velocity vectors before and after the collision may have both horizontal and vertical components
When solving problems involving collisions in two dimensions:
- identify the objects included in the system, making sure there are no net external forces
- write expressions for the x- and y- components of the momentum of each object before and after the collision
- write expressions for the total momentum of the system in each direction before and after the collision
- apply the conservation of momentum principle to each direction separately
- solve for the unknown quantity using Pythagoras' theorem

A collision in two dimensions between two objects A and B. Before the collision, object A moves towards stationary object B with velocity v0A. After the collision, object A moves away at an angle θA above the horizontal with velocity vA and object B moves away at an angle θB below the horizontal with velocity vB. — **During a collision in two dimensions between two objects, A and B, they move off in different directions after the collision**

If no external forces act on a system, horizontal and vertical components of momentum are conserved
Applying the conservation of momentum principle:

$m_{A} {\vec{v}}_{0 A} = m_{A} {\vec{v}}_{A} + m_{B} {\vec{v}}_{B}$

The components of the velocities in the x-direction are:

$m_{A} v_{0 A} = m_{A} v_{A} \cos θ_{A} + m_{B} v_{B} \cos θ_{B}$

The components of the velocities in the y-direction are:

$0 = m_{A} v_{A} \sin θ_{A} - m_{B} v_{B} \sin θ_{B}$

For a collision in two dimensions between two objects A and B, the velocities must be resolved into x- and y- components. Object A moves away at an angle θA above the horizontal with velocity vA, so it has a velocity of vAcosθA in the x-direction and vAsinθA in the y-direction. Object B moves away at an angle θB below the horizontal with velocity vB, so it has a velocity of vBcosθB in the x-direction and vBsinθBin the y-direction. — **To solve problems involving collisions in two dimensions, velocity vectors must be resolved into their horizontal and vertical components**

Worked Example

A particle moves to the right and collides with a stationary particle. The direction of the second particle after the collision is shown below.

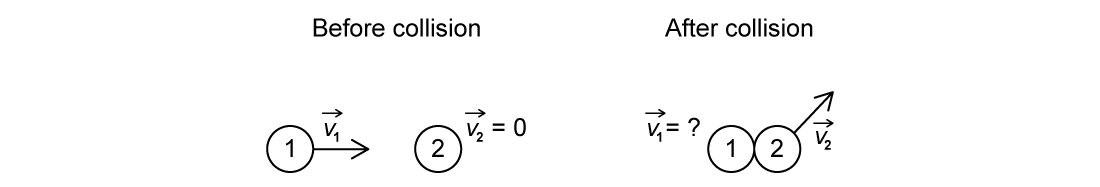
Two particles labeled 1 and 2 before and after a collision. Before the collision, particle 1 moves right with velocity v1, particle 2 is stationary. After the collision, particle 2 changes direction and particle 1's direction is unknown.

Which of the following is a possible direction of the first particle after the collision?

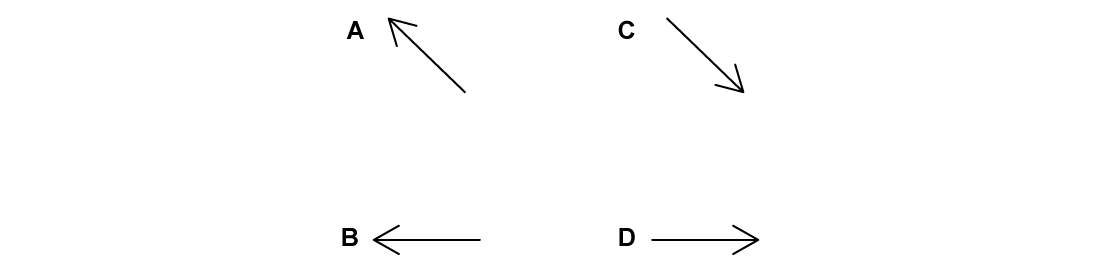
Four arrows labeled A, B, C, and D. A points up-left, B points left, C points down-right, and D points right.

The correct answer is C

Answer:

Step 1: Analyze the scenario

Before the collision, the total momentum is directed horizontally, as momentum is in the same direction as the velocity
The total momentum of the system must be conserved
Therefore, the net momentum after the collision must also be horizontal

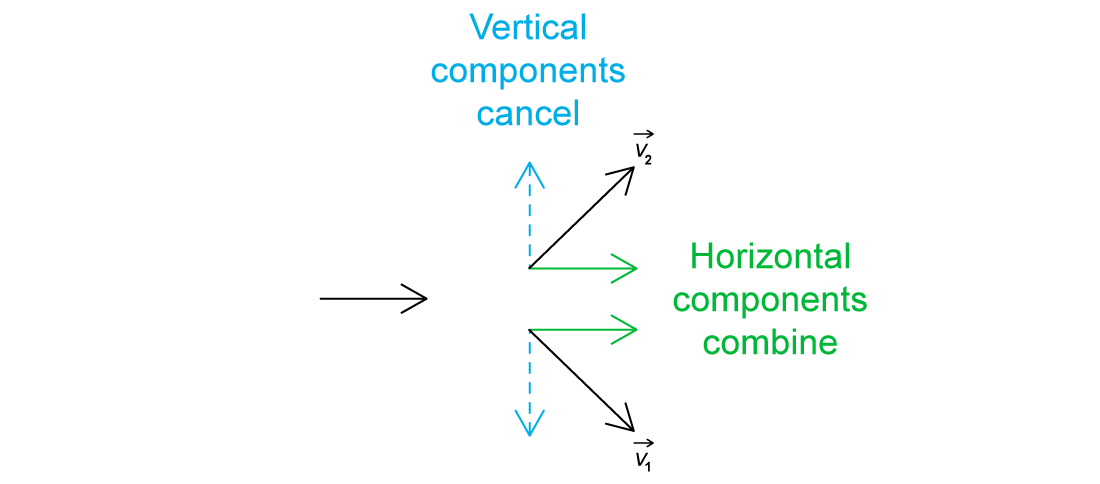
Step 2: Apply the principle of conservation of momentum

Since particle 2 is moving up after the collision, particle 1 must move down at the same angle to cancel out the vertical component of the momentum
This is shown by option C

Vector components are shown: a leftward arrow splitting into two angled vectors. Vertical components cancel, horizontal components combine.

Examiner Tip

In AP Physics 1 you will be expected to tackle conservation of momentum problems in one dimension both quantitatively and qualitatively, whereas for problems in two dimensions, you will only be expected to tackle these qualitatively and semiquantitatively.

Exam questions will predominantly be focused on your ability to set up the equations properly and reason about how changing a given mass, speed, or angle would affect other quantities.

In AP Physics 2, you will be expected to solve conservation of momentum problems in two dimensions that include one unknown final velocity, so it's worth getting to grips with the mathematics involved now.

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?